
1DV bottom boundary layer modeling under combined wave and
current: Turbulent separation and phase lag effects
Katell Guizien,
1,4
Marjolein Dohmen-Janssen,
2
and Giovanna Vittori
3
Received 9 January 2002; revised 3 September 2002; accepted 21 November 2002; published 28 January 2003.
[1] On the basis of the Wilcox [1992] transitional k- w turbulence model, we propose a new
k-w turbulence model for one-dimension vertical (1DV) oscillating bottom boundary layer
in which a separation condition under a strong, adverse pressure gradient has been
introduced and the diffusion and transition constants have been modified. This new
turbulence model agrees better than the Wilcox original model with both a direct
numerical simulation (DNS) of a pure oscillatory flow over a smooth bottom in the
intermittently turbulent regime and with experimental data from Jensen et al. [1989], who
attained the fully turbulent regime for pure oscillatory flows. The new turbulence model is
also found to agree better than the original one with experimental data of an oscillatory
flow with current over a rough bottom by Dohmen-Janssen [1999]. In particular, the
proposed model reproduces the secondary humps in the Reynolds stresses during the
decelerating part of the wave cycle and the vertical phase lagging of the Reynolds stresses,
two shortcomings of all previous modeling attempts. In addition, the model predicts
suspension ejection events in the decelerating part of the wave cycle when it is coupled
with a sediment concentration equation. Concentration measurements in the sheet flow
layer give indication that these suspension ejection events do occur in practice.
INDEX
TERMS: 4211 Oceanography: General: Benthic boundary layers; 4560 Oceanography: Physical: Surface waves
and tides (1255); 4568 Oceanography: Physical: Turbulence, diffusion, and mixing processes; 4842
Oceanography: Biological and Chemical: Modeling; 4558 Oceanography: Physical: Sediment transport;
K
EYWORDS: turbulence, modeling, wave boundary layer, sediment dynamics
Citation: Guizien, K., M. Dohmen-Janssen, and G. Vittori, 1DV bottom boundary layer modeling under combined wave and current:
Turbulent separation and phase lag effects, J. Geophys. Res., 108(C1), 3016, doi:10.1029/2001JC001292, 2003.
1. Introduction
[2] In coastal zones, the suspension associated to waves
and currents in the bottom boundary layer can have an
impact on both human activities and ecological equilibrium.
Indeed, it is well known that suspension plays a major role in
sediment transport and affects human works and biological
species through morphodynamical changes, which may
affect the stability of the former and destroy the habitats of
the latter. Moreover suspension can also affect directly the
life cycle of some species and hence play a role in their
population dynamics. This is the case for instance for benthic
invertebrates with plan ktonic l arvae. Ind eed, the larvae
settlement on the bed may be limited by strong suspension
events and lead to dramatic cut in the population. Studying
the suspension dynamics under waves and currents is hence
of great interest, especially over flat bed since this corre-
sponds to the more severe hydrodynamical conditions.
[
3] As a conclusion of the MAST II G8-M Coastal
Morphodynamics European project, some shortcomings in
modeling sand transport by combined waves and currents
have been identified which are reported by Davies et al.
[1997]. In their paper, an intercomparison of experimental
data with four research sediment transport models under
combined waves and currents was presented . The four
models mainly differed in the complexity of the turbulence
closure schemes (from zero to two-equations) used to
compute the eddy-viscosity in the bottom turbulent boun-
dary layer. In Fredsøe’s [1984] model, a time-dependent
eddy viscosity is derived from integration of the momentum
equation over the wave boundary layer, assuming a loga-
rithmic velocity profile (zero-equation model). Ribberink
and Al Salem [1995] used a time- and height-dependent
eddy viscosity by extending Prandtl’s mixing length theory
to an unsteady flow (zero-equation model). Li and Davies
[1996] used a k-equation model with a similarity l-scaling
(one-equation model) and Huynh Than et al. [1994] used a
k-L model (two-equation model) to compute a time-varying
eddy visc osity. The concent rati on is computed from a
convection-diffusion equation in which vertical sediment
diffusivity is assumed to be equal to the time-dependent
eddy viscosit y, except in the Huynh Than et al. model where
JOURNAL OF GEOPHYSICAL RESEARCH, VOL. 108, NO. C1, 3016, doi:10.1029/2001JC001292, 2003
1
Laboratoire des Ecoulements Ge´ophysiques et Industriels, Grenoble
Cedex 9, France.
2
Department of Civil Engineering, University of Twente, Enschede,
Netherlands.
3
Dipartimento di Ingegneria Ambientale, Universita` di Genova, Genoa,
Italy.
4
Now at Laboratoire d’Oce´anographie Biologique de Banyuls, Banyuls
sur Mer Cedex, France.
Copyright 2003 by the American Geophysical Union.
0148-0227/03/2001JC001292$09.00
16 - 1

turbulence damping is taken into account so that eddy
viscosity and sediment diffusivity are related through some
coupling terms. Despite the difference in the complexity of
the turbulence closure, all the models show similar short-
comings when predictions are compared to flat bed experi-
ments which correspond to strong wave plus current
conditions (‘‘sheet flow’’ regime).
[
4] All the models lead to underestimation of the phase
lag between concentration and velocity in the upper part of
an oscillatory boundary layer and to unreliable estimates of
sediment load p redictions. Recent experiments in clear
water (without sediment) by Dohmen-Janssen [1999] show
a relevant phase lag over depth in Reynolds stress time
series thus showing that the phase lag between concentration
and velocity is partially inherent to the oscillatory boundary
layer dynamics and not totally due to the sediment feedback
on the turbulence structure. Therefore, efforts should be
done to improve turbulence modeling for oscillatory boun-
dary layers before working on flow and sediment coupling.
[
5] In particular, none of the aforementioned models
reproduce correctly the phase lag between Reynolds stress
and velocity. This phase lag is related to the Reynolds stress
vertical decay in the region far from the wall: the quicker it
decays, the larger the phase lag is. In a recent paper, Sana
and Tanaka [2000] present a comparison between five low-
Reynolds-number k- models and the direct numerical
simulation (DNS) by Spalart and Baldwin [1989] for sinus-
oidal oscillatory flows over smooth beds. They show that
the Jones and Launder’s [1972] model provides better
predictions of transition initiation and of the Reynolds stress
vertical decay in the region far from the wall. These results
suggest that the introduction of low-Reynolds-number mod-
ifications could improve the modeling of phase lag between
Reynolds stress and velocity. However, it should also be
pointed out that Jones and Launder’s model underestimates
the peak value of the turbulent kinetic energy and over-
estimates the bottom shear stress enhancement after tran-
sition. It can be concluded that none of the low-Reynolds-
number modifications proposed in these five k-e models
enable to predict correctly the whole dynamics of the
oscillating boundary layer.
[
6] A second shortcoming of the models considered by
Davies et al. [1997] concerns concentration secondary
peaks which are sometimes observed near flow reversal in
experimental measurements close to the bottom [Katapodi
et al., 1994; Dohmen-Janssen, 1999] and are not repro-
duced by models. Although the very sharp concentration
peaks that show in the measurements close to the bottom
may be partly caused by the measuring technique, there are
indications that suspension ejection events really occur
before flow reversal (see section 4). These may be attributed
to shear instabilities in the wave boundary layer [Foster et
al., 1994].
[
7] The contribution of these secondary concent ration
peaks to the near-bed sediment load is limited, since they
occur at a time when the velocity is nearly zero. However,
the huge amount of sediment picked up from the bed around
flow reversal, especially for fine sand, may affect turbulence
and at the same time may be redistributed along time in the
upper suspension layer. Hence, these concentration secon-
dary peaks can be of great importance with respect to total
sediment load predictions. Besides, such suspension ejec-
tion events can play a crucial role in benthic life.
[
8] Savioli and Justesen [1996] proposed a modified
condition for the reference concentration that enables to
reproduce secondary peaks on the concentration time series
with a standard (without low-Reynolds-number effects) k-
model [Rodi, 1980] in a one-dimensional vertical (1DV)
fully rough turbulent oscillating boundary layer model,
Figure 1. Phase j definition along the oscillatory part of
the outer flow velocity ( –) and corresponding pressure
gradient (- -).
Figure 2. Phase-averaged Reynolds stress time series
obtained using the new k - w model for (a) b
sep
ranging from
4to40(w
vortex
= 300) and (b) w
vortex
ranging from 30 to
3000 (b
sep
= 20) (R
d
= 2179, R
e
=2.4 10
6
, A/k
N
= 3173).
16 - 2 GUIZIEN ET AL.: 1DV BOTTOM BOUNDARY LAYER MODELING UNDER COMBINED WAVE AND CURRENT

taking advantage of a narrow diffusivity peak just before
flow reversal. A much smaller narrow peak, is also present
near flow reversal in the eddy viscosity time series com-
puted using a standard k-w turbulence model [Wilcox, 1988],
whereas a k-L turbulence model [Huynh Than et al., 1994]
does not produce such peaks. However, although showing
discrepancies on the eddy viscosity time series, the three
turbulence models produce similar time series of the bottom
shear stress, without any significant increase near flow
reversal [Guizien et al., 2001]. In fact, differences in the
eddy viscosity time series are due to the closures of the
models, namely to the singularity in the behavior of the
eddy viscosity, that reads n
T
= k/w in the k-w model and
n
T
= 0.09 k
2
/ in the k- model. The singularity arises when k
and the other value w or approach zero, for instance when
the outer flow velocity decreases to zero during a wave
cycle. At that phase, t he instantaneous local Reynolds
number decreases rapidly and the eddy viscosity strongly
increases if the fully turbulent value for the model constants
is applied. In steady boundary layers, it is well known that
the constants used in k- standard models should be modified
using low-Reynolds-number damping function to avoid the
singular behavior of the eddy viscosity near the wall when
computing the viscous sublayer. It is worth noticing that, in
standard k-w models, the viscous sublayer can be easily
included for both smooth and rough bottom [Saffman, 1970],
avoiding this latter near-wall singularity. In addition, under
stationary conditions with an adverse pressure gradient and
for low-Rey nolds-numbers, standard k-w models perform
bett er than standard k- models [Wilcox,1998].Thisis
consistent with the fact that the near-reversal eddy viscosity
peak is smaller in the standard k-w computations than in the
standard k- computations and that a much smaller time step
(50 times smaller, strongly depending on the velocity ampli-
tude) is required to deal with the singularity in computations
with a standard k- model compa red to computations per-
formed with a standard k-w model. However, introducing
low-Reynolds-number effect in a k- turbulence model (e.g.,
Chien [1982] model, used by Thais et al. [1999]), the peak in
the eddy viscosity time series for an oscillating boundary
layer vanishes (L. Thais, personal communication, 1999).
Similarly, when using the Wilcox [1992] transitional k-w
turbulence model, that includes low-Reynolds-number
effect, the eddy viscosity time series for oscillating boundary
layers do not present any peak.
[
9] Recently, clear water experiments by Dohmen-Jans-
sen [1999] shed a new light on this question. During these
experiments, stronger turbulent activity was detected in the
Reynolds stress time series close to the wall in the decel-
erating part of the wave cycle. This turbulence enhancement
occurs at phases when the concentration secondary peaks
are observed for the same hydrodynamical conditions. It
should be outlined that fluctuat ions similar to the ones
measured by Dohmen-Janssen were observed by Sleath
[1987]. He also measured a 180 phase shift of the phase
of the Reynolds stress maximum at a certain height from the
bed and explained it by assuming the existence of jets of
fluids associated with vortex formation over the bottom
roughness. He suggested that these jets of fluid would
dominate the flow close to the wall whereas turbulence
would dominate far from it. This explanation clearly implies
that a d etailed modeling of rough oscillating boundary
layers should be three-dimensional and include a mecha-
nism for vortex generation by bottom roughness. Even
though such a sophisticated model is beyond the scope of
this paper, it is clear that the strong turbulence activity
which takes place during the decelerating phases of the
cycle should be taken into account since it contributes to put
more sediment in suspension. In this paper, starting from the
Wilcox [1992] transitional k-w model, a new transitional k-w
turbulence model is proposed in order to improve the 1DV
modeling of oscillating bottom boundary layers. A k-w
turbulence model is preferred to a k- one for its simplicity,
its ability to include the viscous sublayer and for its good
predictions under adverse pressure gradients, which occur
during the decelerating pha ses of the wave cycle. The
improvement brought to the Wilcox transitional k-w model
concerns vertical phase lagging and suspension ejection
events. The damping of turbulence by the stratification is
Figure 3. Velocity vertical profiles at different phases (a)
and bottom shear stress time evolution (b) computed by
DNS (...), the original Wilcox transitional k- w model (- -)
and the new k-w model (—) for a sinusoidal outer flow U =
U
0
sin(2pt/T ) with T =4s,U
0
= 1.1 m/s over a smooth
bottom (R
d
= 1241, R
e
=7.7 10
5
).
GUIZIEN ET AL.: 1DV BOTTOM BOUNDARY LAYER MODELING UNDER COMBINED WAVE AND CURRENT 16 - 3

Figure 4. Reynolds stress vertical profiles at different phases: (a) j = 45,(b)j =0,(c)j =45, and
(d) j =90 computed by DNS (...), the original Wilcox transitional k-w model (- -) and the new k-w
model (—) for a sinusoidal outer flow U = U
0
sin(2pt/T ) with T =4s,U
0
= 1.1 m/s over a smooth bottom
(R
d
= 1241, R
e
=7.7 10
5
).
Figure 5. Turbulent kinetic energy vertical profiles at different phases: (a) j = 45,(b)j =0,(c)j =
45, and (d) j =90 computed by DNS (...), the original Wilcox transitional k-w model (- -), and the new
k-w model (—) for a sinusoidal outer flow U = U
0
sin(2pt/T) with T =4s,U
0
= 1.1 cm/s over a smooth
bottom (R
d
= 1241, R
e
=7.7 10
5
).
16 - 4 GUIZIEN ET AL.: 1DV BOTTOM BOUNDARY LAYER MODELING UNDER COMBINED WAVE AND CURRENT
also introduced. The model is presented in section 2. The
ability of the new model to predict laminar-turbulent tran-
sition is tested for a pure oscillatory flow over a smooth
bottom by comparison with direct numerical simulations in
section 3.1 and with the experimental data from Jensen et
al. [1989] in section 3.2. The model is then compared with
experimental data in the rough turbulent regime for an
oscillatory flow plus current in section 4.1 [Dohmen-Jans-
sen, 1999]. Finally, concentration predictions corresponding
to these latter hydrodynamical conditions are described in
section 4.2.
2. The New k-W Model
2.1. Basic Formulation
[
10] The basis of the Reynolds Averaged Navier-Stokes
(R.A.N.S.) model we use to compute the turbulent bottom
boundary layer under an oscillatory flow (with or without
current) is the transitional k-w model devised by Wilcox
[1992] in its 1DV formulation. In addition, turbulence
damping by stratification is introduced into the original
Wilcox formulation through coupling terms between turbu-
lence and the density field r(z, t)=r
0
+ C(z, t)(r
s
r
0
)
resulting f rom the sediment susp ension (r
0
is the fluid
density, r
s
is the sediment density and C(z, t) is the sediment
concentration per volume). The coupling terms are similar
to those introduced by Lewellen [1977] in a k-L model. The
hydrodynamical model (i.e., without sediment) is easily
retrieved taking @r/@z =0.
[
11] The horizontal velocity u inside the boundary layer,
the turbulent kinetic energy k and the energy dissipation rate
w fulfill the following set of equations (1) –(6), where U is
the horizontal velocity outside the boundary layer (outer
flow) and
@
P
@x
is the mean pressure gradient generating the
current (note that for pure oscillatory flow,
@
P
@x
¼ 0). In this
1DV for mulatio n, we assume n o x-dependence for all
averaged quantities (no horizontal convective or diffusive
transport) and no vertical velocity at the top of the boundary
layer. These assumptions correspond strictly to the tunnel
experiment conditions we will compare with in the next
sections.
@u
@t
¼
1
r
0
@
P
@x
þ
@U
@t
þ
@
@z
n þ n
t
ðÞ
@u
@z
ð1Þ
@k
@t
¼ n
t
@u
@z
2
b*kw þ
@
@z
n þ s*n
t
ðÞ
@k
@z
þ
g
r
0
g
t
@r
@z
ð2Þ
@w
@t
¼an
t
w
k
@u
@z
2
|fflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflffl}
production
bw
2
|{z}
dissipation
þ
@
@z
nþsn
t
ðÞ
@w
@z
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
diffusion
þc
0
w
2k
g
r
0
g
t
@r
@z
|fflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflffl}
buoyancy
ð3Þ
n
t
¼ a*
k
w
1 C
3
1 C
1
ðÞ1 C
2
ðÞ
ð4Þ
g
t
¼ n
t
1 C
2
1 C
3
ðÞ
ð5Þ
¼ 2
g
r
0
dr
dz
4
w
2
ð6Þ
with
a* ¼
a
0
*
þ Re
T
=R
K
1 þ Re
T
=R
K
; a ¼
13
25
a
0
þ Re
T
=R
w
1 þ Re
T
=R
w
a*ðÞ
1
;
b* ¼
9
100
4=15 þ Re
T
=R
b
4
1 þ Re
T
=R
b
4
where Re
T
¼
k
nw
; b ¼ b
0
¼
9
125
; a
0
*
¼
b
0
3
; a
0
¼
1
9
, R
w
= 2.95,
and c
0
= 0.8. It should be recalled here that, unlike most of
the above coefficients, no simple argument can be found to
estimate the values for s, s*, R
K
and R
b
. For given values
for R
K
and R
b
, there is a unique value of R
w
that yields the
value measured by Nikuradse of the constant appearing in
the law of the wall for smooth wall C
w
= 5.0. Hence, Wilcox
[1992] proposed values for R
K
=6,R
b
= 8 and s = s*=0.5
that give the best agreement both with experiments and
direct numerical simulations of steady boun dary layers with
and without adverse or favorable pressure gradient.
However, he already outlined that taking a smaller value
for s* should improve the model’s prediction for boundary
layers with variable pressure gradient. Hence, on the basis
of a preliminary analysis of the performances of the model
we suggest to use the following values for oscillatory
boundary layers (oscillatory pressure gradient): s = 0.8, s*=
0.375, R
K
= 20 and R
b
= 27. The original value for R
w
=
2.95 is kept and gives a constant for the law of the wall
C
w
= 7.6 for a steady boundary layer in the smooth regime.
These values provide better predictions than the values
Figure 6. Half-period bottom shear stress time series
showing laminar-turbulent transition for increasing Rey-
nolds number predicted by the original Wilcox transitional
k-w model (- -) and the new k-w model (—) for a sinusoidal
outer flow over a smooth bottom.
GUIZIEN ET AL.: 1DV BOTTOM BOUNDARY LAYER MODELING UNDER COMBINED WAVE AND CURRENT 16 - 5

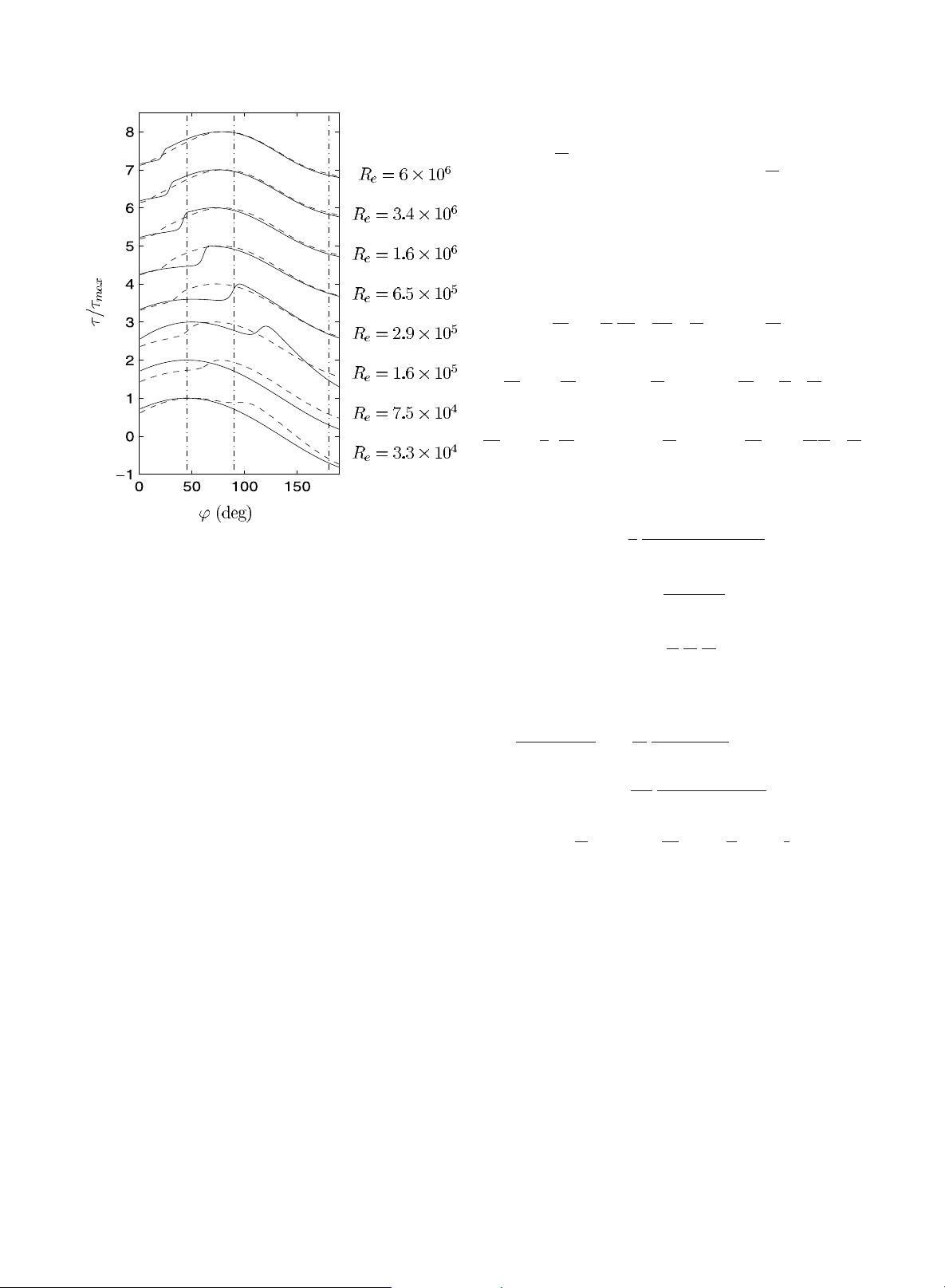
![Figure 12. Phase-averaged Reynolds stress time series at different levels from the bed measured by Dohmen-Janssen [1999, exp. G5] (. . .), obtained using the original Wilcox transitional k-w model (- -) and the new k-w model (—) (Rd = 1453, Re = 1.06 106, A/kN = 2115).](/figures/figure-12-phase-averaged-reynolds-stress-time-series-at-kkx9dkxo.png)

![Figure 7. Bottom shear stress measured by Jensen et al. [1989] (. . .), the original Wilcox transitional kw model (- -) and the new k-w model (—) for a sinusoidal outer flow U = U0 sin(2pt/T ) with T = 9.72 s over a smooth bottom for different Reynolds number.](/figures/figure-7-bottom-shear-stress-measured-by-jensen-et-al-1989-11d36agr.png)
![Figure 8. Velocity vertical profiles at different phases during the accelerating part of the cycle (a) and during the decelerating part of the cycle (b) measured by Jensen et al. [1989, test 8] (. . .), computed with the original Wilcox transitional k-w model (- -) and the new k-w model (—) for a sinusoidal outer flowU =U0 sin(2pt/T) with T = 9.72 s,U0 = 1.02 m/s over a smooth bottom (Rd = 1789, Re = 1.6 106).](/figures/figure-8-velocity-vertical-profiles-at-different-phases-27t7wojm.png)
![Table 1. Experimental Conditions for Dohmen-Janssen [1999] Clear Water Experiments and Janssen et al. [1997] Sand Experiments](/figures/table-1-experimental-conditions-for-dohmen-janssen-1999-18pr9klj.png)