© 2010 IEEE. Reprinted, with permission, from Tuan Hoang, 2-D two-fold symmetric circular shaped filter design
with homomorphic processing application, Acoustics Speech and Signal Processing (ICASSP), 2010 IEEE
International Conference on, March 2010. This material is posted here with permission of the IEEE. Such permission
of the IEEE does not in any way imply IEEE endorsement of any of the University of Technology, Sydney's products
or services. Internal or personal use of this material is permitted. However, permission to reprint/republish this
material for advertising or promotional purposes or for creating new collective works for resale or redistribution must
be obtained from the IEEE by writing to pubs-permissions@ieee.org. By choosing to view this document, you agree to
all provisions of the copyright laws protecting it
2-D TWO-FOLD SYMMETRIC CIRCULAR SHAPED FILTER DESIGN WITH
HOMOMORPHIC PROCESSING APPLICATION
A. J. Seneviratne, H. H. Kha, H. D. Tuan
School of Electrical Engineering
and Telecommunication,
University of New South Wales,
Sydney, NSW 2052, Australia.
T. Q. Nguyen
Department of Electrical and
Computer Engineering,
University of California in San Diego,
9500 Gilman Dr., La Jolla CA 92093-0407 USA.
ABSTRACT
A design method of a linear-phased, two-dimensional (2-D), two-
fold symmetric circular shaped filter is presented in this paper. Al-
though the proposed method designs a non-separable filter, its imple-
mentation has linear complexity. The shape of the passband and the
stopband is expressed in terms of level sets of second order trigono-
metric polynomials. This enables the transformation of the filter
specifications to a Semi-Definite Program (SDP) of moderate di-
mension. The proposed filter outperforms currently available filter
design methods. We present a performance comparison, as well as a
homomorphic processing image enhancement example to illustrate
the effectiveness of this method.
Index Terms— Two-fold symmetric, Two-dimensional Circular
shaped filter, Semi-definite program, Trigonometric polynomials,
1. INTRODUCTION
There are many different approaches in designing 2-D filters, each
with its pros and cons. The simplest method is in the form of a
separable filter [1] which is developed as a product of two 1-D fil-
ters. They are favored in applications which require very high order
filters since their complexity is very low. However there is limited
freedom with the design variables and it is confined to rectangu-
lar shape. Non-separable filters are preferred when designing dif-
ferently shaped filters but their design is much more challenging.
McClellan transform [2], [3] can be used to develop non-separable
filters using 1-D filters. Their complexity is very low but it is not
possible to control the filter characteristics such as passband shape
and cut-off frequency. This is mainly because there is no direct way
to find the 1-D filter that, when transformed, will produce the desired
2-D filter.
Frequency sampling method [4] gives better control over the
passband shape and produces lower peak ripples. However the com-
plexity is very high and many difficulties such as singularities and
numerical instability arise in the implementation of these filters. The
greatest barrier in designing filters with desired characteristics is in
the handling the semi-infinite constraints that arise due to the peak
passband and stopband ripple constraints. Classical minmax filters
[5] deal with this by approximating them by linear constraints calcu-
lated at samples of the frequency plane.
Recently SDP has been employed to deal with these semi-
infinite constraints. There have been continues interest in represent-
ing the passband and stopband by trigonometric polynomials that are
positive in the region of interest. Initially first order trigonometric
polynomials have been used to design two-fold symmetric filters [6].
However they did not consider the circular shape and they have not
presented a direct relationship between the filter specifications and
the coefficients of the polynomials. The resulting SDP formulation
is of very high dimension.
SDP formulations of moderate dimension have been achieved
in four-fold symmetric filter designs [7], [8]. Although they have
linear complexity in implementation, the trigonometric polynomi-
als used do not approximate the passband and stopband shapes as
well as one would hope for. This problem has been addressed in
[9] where circular shaped passband and stopband has been success-
fully expressed by level sets of simple second order trigonometric
polynomials. They have clearly presented the relationship between
the desired filter characteristics and coefficients of the trigonometric
polynomials.
The paper [9] is based on four-fold symmetric filters and we
will extend this to a more general case of two-fold symmetric fil-
ters in this paper. Two-fold symmetric filters present more flexibility
in the design variables and, therefore, the design procedure becomes
more challenging. However since the optimization is performed over
greater number of variables the filter performance can be improved
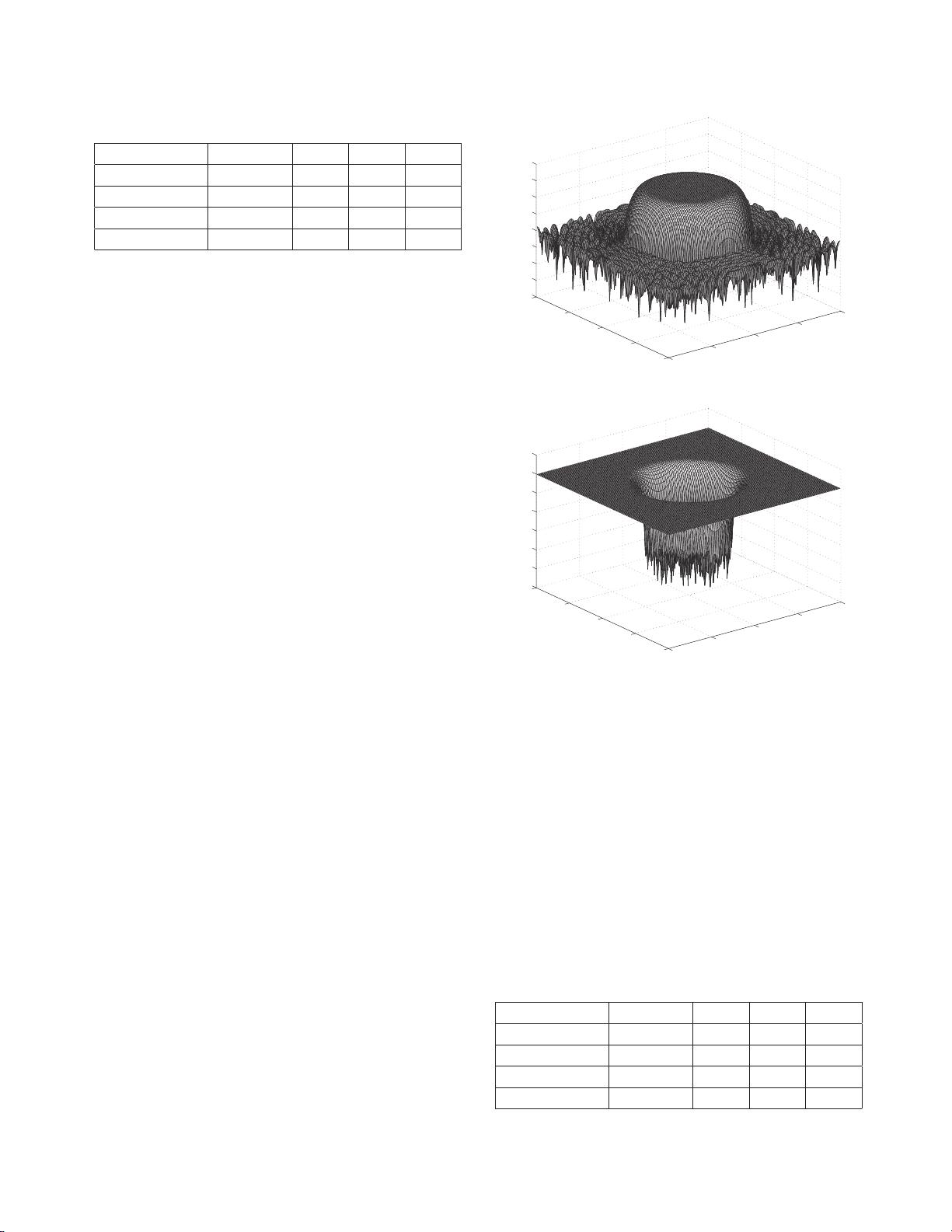
in terms of frequency selectivity. Circular filters are of great impor-
tance in two-dimensional signal processing but they have not been
given proper attention so far. Thus design and implementation of
two-fold symmetric circular shaped filter are discussed in this pa-
per followed by an example of homomorphic processing application.
Standard mathematical notations are used in this paper, except that
A
A
A refers to the trace of a matrix and the elements of a matrix are
given as A
A
A =[a
ij
]
n
i,j=0
.
2. TWO-FOLD SYMMETRIC 2-D FILTER DESIGN
The frequency response of a zero-phased digital filter is a real val-
ued function and its impulse response is symmetric about the origin
h(n, n)=h(−n, −n) [10]. Thus the Z-transform of a (2n +1)×
(2n +1), zero-phase, two-fold symmetric, two-dimensional filter
can be written as follows
H(z
1
,z
2
)=h
nn
+
n
l=1
h
(n+l)n
(z
l
1
+ z
−l
1
)
+
n
l=−n
n
i=1
h
(n+l)(n+i)
(z
l
1
z
i
2
+ z
−l
1
z
−i
2
). (1)
3694978-1-4244-4296-6/10/$25.00 ©2010 IEEE ICASSP 2010
Its Fourier transform can be obtained by evaluating on the unit circle
{(z
1
,z
2
)=(e
jω
1
,e
jω
2
), Ω:=(ω
1
,ω
2
) ∈ [−π, π] × [0,π]},
H(Ω)=
n
i=0
n
l=0
x
il
cos(iω
1
+lω
2
)+
n
i=0
n
l=0
y
il
cos(iω
1
−lω
2
), (2)
= X
X
X,M
1
M
1
M
1
(Ω) + Y
Y
Y,M
2
M
2
M
2
(Ω), (3)
where M
1
M
1
M
1
(Ω)= [cos(iω
1
+lω
2
)]
n
i,l=0
, M
2
M
2
M
2
(Ω)= [cos(iω
1
−lω
2
)]
n
i,l=0
,
X
X
X =[x
il
]
n
i,l=0
and Y
Y
Y =[y
il
]
n
i,l=0
.
The design objective is to find the coefficients of the matrix X
X
X
and Y
Y
Y such that the desired frequency response is obtained. There
are 2(n +1)
2
design variables, which is twice as that of the four-
fold symmetric filter. Although this makes the design of a two-fold
symmetric filter more challenging, the filter performance can be im-
proved in terms of frequency selectivity since the optimization is
performed over a larger number of variables. In this paper the filter
order is taken as n. Depending on the application and the data to be
processed the filter specifications vary considerably. Generally filter
specifications can be formulated as a minimum stopband attenuation
problem as follows:
min
X,Y
X,Y
X,Y ,δ
s
δ
s
(4a)
s.t. |H(Ω) − 1|≤δ
p
, ∀Ω ∈ Ω
p
(4b)
|H(Ω)|≤δ
s
, ∀Ω ∈ Ω
s
, (4c)
where δ
p
and δ
s
are the passband ripple and the stopband attenuation
respectively. The constraints given in (4b) and (4c) are semi-infinite
constraints and pose the greatest challenge in designing the desired
filter. In the next section we consider an effective method of trans-
forming this optimization problem in to an SDP of linear complexity.
3. CIRCULAR SHAPED FILTER DESIGN
The passband and the stopband of a circular shaped filter can be
specified as follows:
Ω
p
= {(ω
1
,ω
2
) ∈ [−π, π] × [0,π]:ω
2
1
+ ω
2
2
≤ ω
2
p
}, (5)
Ω
s
= {(ω
1
,ω
2
) ∈ [−π, π] × [0,π]:ω
2
1
+ ω
2
2
≥ ω
2
s
}. (6)
It is very difficult to represent the circular shape in the form of
trigonometric polynomials. Circular shape has not been attempted in
[6] and the polynomials used in [8] do not produce the desired shape.
However it has been proven in [9] that the passband and the stopband
of the form (5) and (6) can be exactly described by level sets of sec-
ond order trigonometric polynomials of the following form,
T (Ω) = a(cos 2ω
1
+ cos 2ω
2
)+b(cos ω
1
+ cos ω
2
)+c. (7)
Coefficients a,b and c in Equation (7) have to be found such that
its level sets closely represents the circular shape given in (5) and
(6). Since the trigonometric polynomial of the form of (7) has been
proven to be a successful method of representing the circular shape,
the same mask will be used in this paper. The following least squares
optimization problem can be used to find the coefficients of (7).
min
x=(a,b,c)
T
,||x||=1
ω
α
/
√
2
0
x
T
⎡
⎣
cos 2ω
1
+ cos 2
ω
2
α
− ω
2
1
cos ω
1
+ cos
ω
2
α
− ω
2
1
1
⎤
⎦
⎡
⎣
cos 2ω
1
+ cos 2
ω
2
α
− ω
2
1
cos ω
1
+ cos
ω
2
α
− ω
2
1
1
⎤
⎦
T
xdω
1
, (8)
with α ∈{p, s}. The normalized eigenvector of the minimum eigen-
value of the following matrix will give the solution x =(a, b, c)
which minimizes the optimization problem defined in (8).
ω
α
√
2
0
⎡
⎣
cos2ω
1
+cos2
ω
2
α
−ω
2
1
cosω
1
+cos
ω
2
α
−ω
2
1
1
⎤
⎦
⎡
⎣
cos2ω
1
+cos2
ω
2
α
−ω
2
1
cosω
1
+cos
ω
2
α
−ω
2
1
1
⎤
⎦
T
dω
1
. (9)
Generally the minimum eigenvalue of the matrix (9) is zero or nearly
zero. This confirms the fact that the second order trigonometric poly-
nomials of the form (7) exactly describes the circular shaped pass-
band and the stopband. Thus two trigonometric polynomials can be
derived to represent the passband and the stopband.
T
α
(Ω)= a
α
(cos 2ω
1
+cos 2ω
2
)+b
α
(cos ω
1
+cos ω
2
)+c
α
, (10)
with α ∈{p, s}. The next step is to define a family of trigonometric
polynomials using the Chebyshev recursion.
If T
0
(Ω) =1,
T
1
(Ω) =A + B cos ω
1
+ C cos ω
2
+ D cos(ω
1
+ ω
2
)
+ E cos(ω
1
− ω
2
), (11)
with predefined coefficients A,B,C,D and E, then T
j
(Ω),j =2, 3, ...
can be derived using Chebyshev recursion as follows,
T
j
(Ω) =2T
(j−1)
(Ω)T
1
(Ω) − T
(j−2)
(Ω). (12)
Here it should be noted that more complicated class of trigonometric
polynomials of the form {cos(jω
1
+kω
2
),j,k =−n, .., −1, 0, 1, ...n}
are used in this paper than that used in [9] to facilitate the two fold
symmetry. However our results show that this leads to improvement
of the performance of the filter. Using the set of trigonometric poly-
nomials derived using (11) and (12) a moment matrix is defined as
follows,
Ψ
Ψ
Ψ(Ω) =
⎡
⎢
⎢
⎢
⎣
1
T
1
(Ω)
.
.
.
T
m
(Ω)
⎤
⎥
⎥
⎥
⎦
⎡
⎢
⎢
⎢
⎣
1
T
1
(Ω)
.
.
.
T
m
(Ω)
⎤
⎥
⎥
⎥
⎦
T
,m=[(n − 2)/2]. (13)
Since T
α
(Ω) ≥ 0, ∀Ω ∈ Ω
α
and since Ψ
Ψ
Ψ(Ω) is a positive definite
matrix, T
α
(Ω)Ψ
Ψ
Ψ(Ω) ≥ 0, ∀Ω ∈ Ω
α
. This result can be used to de-
fine cone constraints which represent the passband and the stopband
of the filter,
C
α
={(X, Y
X, Y
X, Y ),X
X
X ∈ R
(n+1)×(n+1)
,Y
Y
Y ∈ R
(n+1)×(n+1)
:
X
X
X,M
1
M
1
M
1
(Ω) + Y
Y
Y,M
2
M
2
M
2
(Ω)≡
ˆ
X
α
ˆ
X
α
ˆ
X
α
,T
α
(Ω)Ψ
Ψ
Ψ(Ω),
ˆ
X
α
ˆ
X
α
ˆ
X
α
≥ 0,α ∈{p, s}}. (14)
Thus the semi-infinite program given by (4a),(4b) and (4c) can be
transformed in to a semi-definite program as follows:
min
X,Y
X,Y
X,Y ,δ
s
δ
s
(15a)
s.t.
X
X
X − (1 − δ
p
)E
E
E,Y
Y
Y
∈ C
p
(15b)
− X
X
X +(1+δ
p
)E
E
E,−Y
Y
Y
∈ C
p
(15c)
X
X
X − (δ
s
)E
E
E,Y
Y
Y
∈ C
s
(15d)
− X
X
X +(δ
s
)E
E
E,−Y
Y
Y
∈ C
s
, (15e)
where E
E
E ∈ R
(n+1)×(n+1)
has zero entries except E
E
E(0, 0) = 1.
The passband defined by (5) can be sampled, and for each sample
3695
Table 1. Lowpass circular shaped filters with (ω
p
,ω
s
)=(0.4π,0.6π)
Specifications Our method [9] [8] [3]
Filter order 12 12 25 25
Filter complexity 30 30 96 625
δ
p
0.0106 0.0124 0.0173 0.0257
δ
s
0.0019 0.0036 0.017 0.0248
two constraints can be derived using (15b) and (15c). Similarly two
constraints can be derived for each sample of the stopband (6) by
evaluating expressions (15d) and (15e). Then the coefficients of the
matrix X
X
X and Y
Y
Y have to be found such that it minimizes δ
s
subject to
the constraints derived by sampling the passband and the stopband.
By considering equations (3) and by expanding the expression
given in (14), the following interesting result can be derived to rep-
resent the frequency response of the passband and the stopband.
H(Ω) = T
p
2m
j=0
a
j
T
j
(Ω)+(1− δ
p
) ∀Ω ∈ Ω
p
(16)
H(Ω) = T
s
2m
j=0
a
j
T
j
(Ω) − δ
s
∀Ω ∈ Ω
s
. (17)
It is clear from equations (16) and (17) that the passband and stop-
band can be described by 2m +1waveforms each, which are of the
form {T
α
T
j
,α∈{p, s},j =0, .., 2m}. The number of waveforms
required to describe the passband and stopband of the two-fold sym-
metric filters presented here is the same as that of the four-fold sym-
metric filters presented in [9] and therefore the digital complexity of
both cases are the same(2n +6). However due to the selection of
a more complicated polynomial for T
1
(Ω) in Chebyshev recursion,
the filter performance is improved in two-fold symmetric filters.
4. SIMULATION
In this section we will consider the simulation of a circular shaped
lowpass filter with ω
p
=0.4π, ω
s
=0.6π and of order 24. The
first step is to derive the second order trigonometric polynomials that
represent the passband and the stopband. The eigenvector of the
minimum eigenvalue of the matrix given in (9) was calculated for
ω
α
= ω
p
and ω
α
= ω
s
.
Minimum eigenvalues were zero and the corresponding eigen-
vectors were (a
p
,b
p
,c
p
)=(−0.0488, 0.6108, −0.7903) and
(a
s
,b
s
,c
s
)=(−0.0922, 0.8269, −0.5547) which was then sub-
stituted in equation (10). Select δ
p
as 0.01 and the coefficients of
equation (11) as (A, B, C, D, E)=(0.5, 0.25.0.25.0.125, 0.25).
Semi-definite program was derived as described in Section 3 and
the simulation was performed using optimization software YALMIP
[11] and SDPT3 [12] in MATLAB. Fig. 1 shows the frequency
response of the designed filter in log scale and the performance
comparison with different design methods is given in Table 1.
Highpass circular shaped filters can be designed analogously.
The simulation result of a circular shaped highpass filter with ω
p
=
0.6π, ω
s
=0.4π and of order 36 is shown in Fig. 2. Performance
comparison of different design methods is given in Table 2. In the
case of both lowpass and highpass filter designs, it is clearly evident
that the filter design method presented in this paper has the lowest
complexity and achieves the lowest δ
p
and δ
s
values.
−1
−0.5
0
0.5
1
−1
−0.5
0
0.5
1
−140
−120
−100
−80
−60
−40
−20
0
20
ω
1
ω
2
|H(Ω)| (dB)
Fig. 1. Lowpass circular shaped filter in log scale.
−1
−0.5
0
0.5
1
−1
−0.5
0
0.5
1
−120
−100
−80
−60
−40
−20
0
20
ω
1
ω
2
|H(Ω)| (dB)
Fig. 2. Highpass circular shaped filter in log scale.
5. HOMOMORPHIC PROCESSING SYSTEM
When images with large dynamic range such as natural scenes are
recorded, image contrast can be significantly reduced. Homomor-
phic processing can be used to reduce the dynamic range and to in-
crease the contrast of such images. An image is formed by recording
the light reflected from an object which is illuminated by some light
source. Based on this the model f (n
1
,n
2
)=i(n
1
,n
2
)r(n
1
,n
1
)
can be used to represent the image, where i(n
1
,n
2
) and r(n
1
,n
2
)
represent the illumination and reflection respectively [10].
Since they are combined multiplicatively the components
are made additive by taking the logarithm of the image intensity
f(n
1
,n
2
). The illumination component i(n
1
,n
2
) is related to the
dynamic range of the image and is generally slow varying. So it
can be separated by lowpass filtering log f (n
1
,n
2
). The reflectance
component i(n
1
,n
2
) on the other hand is related to the contrast
Table 2. Highpass circular shaped filters with (ω
p
,ω
s
)=(0.6π,0.4π)
Specifications Our method [9] [8] [3]
Filter order 18 39 25 25
Filter complexity 42 84 96 625
δ
p
0.0003 0.0062 0.0171 0.0248
δ
s
0.0014 0.0026 0.0178 0.0257
3696
within the image and generally vary rapidly. Highpass filtering of
log f(n
1
,n
2
) can be used to extract the reflectance component.
Fig. 3 depicts the complete homomorphic processing system.
The dynamic range can be reduced by decreasing α and the contrast
can be increased by increasing β. This process was implemented
using circular shaped lowpass filter with (ω
p
,ω
s
)=(0.4π, 0.8π)
and highpass filter with (ω
p
,ω
s
)=(0.8π, 0.4π). It was applied
on youtube video with (α, β)=(0.99, 1.5) and the results are
given in Figs. 4 and 5. To see these images more clearly visit
http://ee.unsw.edu.au/∼z3265024/enhancement.html. It can be seen
that the background details are more highlighted in the enhanced im-
age and people standing at the back of the court can be clearly seen.
To evaluate the effectiveness of the homomorphic process the
original image given in Fig. 4 was blurred using a gaussian lowpass
filter before applying the homomorphic process. Then we recovered
the sharpness and the contrast of the original image by changing
the α and β values of the homomorphic process. The PSNR value
between the blurred image and the original image, and that between
the enhanced image and original image was calculated. Results are
given in Fig. 6. This effectively shows that the PSNR value can be
considerably improved by the homomorphic process implemented
using the filters discussed in this paper.
/ŶƉƵƚ
/ŵĂŐĞ
ůŶ
ŝƌĐƵůĂƌ^ŚĂƉĞĚ
>ŽǁƉĂƐƐĨŝůƚĞƌ
ŝƌĐƵůĂƌ^ŚĂƉĞĚ
,ŝŐŚƉĂƐƐĨŝůƚĞƌ
ɴ
ɲ
džƉ
KƵƚƉƵƚ
/ŵĂŐĞ
Fig. 3. Homomorphic system for image enhancement.
Fig. 4. Original image.
Fig. 5. Enhanced image.
Ϭ
ϭϬ
ϮϬ
ϯϬ
ϰϬ
ϱϬ
ϲϬ
ϳϬ
ϴϬ
ϵϬ
Ϭϯ Ϭϰ Ϭϱ Ϭϲ Ϭϳ Ϭϴ ϭ
W^EZͰ;ĚͿ
sĂƌŝĂŶĐĞ
ůƵƌƌĞĚ/ŵĂŐĞ ŶŚĂŶĐĞĚ/ŵĂŐĞ
Fig. 6. PSNR improvement using homomorphic processing.
6. CONCLUSION
A very general approach of designing two-fold symmetric circular
shaped filters with complexity equal to that of a four-fold symmet-
ric filter was presented in this paper. The main advantage is that it
successfully produces the desired circular shape with minimum pass-
band and stopband ripple compared to the currently available design
methods. The coefficients of the polynomial T
1
(Ω) in Chebyshev
recursion have an influence on the filter performance and a method
of selecting optimal values for these coefficients is still open for re-
search.
7. REFERENCES
[1] T. Chen and P. Vaidyanathan, “Recent developments in multidimen-
sional multirate systems,” IEEE Trans. on Circuits and Systems for
Video Technology, vol. 3, pp. 116–137, 1993.
[2] C. Chen and J. Lee, “McClellan transform based design techniques for
two-dimensional linear-phase FIR filters,” IEEE Trans. on Circuits and
Systems I: Fundamental Theory and Applications, vol. 41, pp. 505–
517, 1994.
[3] R. Mersereau, W. Mecklenbrauker, and T. Quatieri, “McClellan trans-
formations for two-dimensional digital filtering-part II: Design,” IEEE
Trans. on Circuits and Systems, vol. 23, pp. 405–414, July 1976.
[4] S. Bagchi and S. Mitra, “The nonuniform discrete Fourier transform
and its applications in filter design. II. 2-D,” IEEE Trans. on Circuits
and Systems II: Analog and Digital Signal Processing, vol. 43, pp. 422–
433, 1996.
[5] J. Hu and L. Rabiner, “Design techniques for two-dimensional digital
filters,” IEEE Trans. on Audio and Electroacoustics, vol. 20, pp. 249–
257, 1972.
[6] B. Dumitrescu, “Trigonometric polynomials positive on frequency do-
mains and applications to 2-D FIR filter design,” IEEE Trans. on Signal
Processing, vol. 54, pp. 4282–4292, 2006.
[7] T. Hung, H. Tuan, B. Vo, and T. Nguyen, “SDP for 2-D filter de-
sign: General formulation and dimension reduction techniques,” Proc.
IEEE Int. Conference on Acoustics, Speech and Signal Processing,
2006 (ICASSP 2006), pp. 621–624, May 2006.
[8] T. Hung, H. Tuan, and T. Nguyen, “Design of diamond and circular fil-
ters by semi-definite programming,” IEEE Int. Symposium on Circuits
and Systems, 2007 (ISCAS 2007), pp. 2966–2969, May 2007.
[9] H. Tuan, K. Fanian, and T. Nguyen, “2-D nonseparable filters of com-
pressed sensing,” Submitted to IEEE Trans. on Image Processing,.
[10] J. S. Lim, Two Dimensional Signal and Image Processing, NJ, US:
Prentice-Hall, 1990.
[11] Y. Lofberg, “Yalmip: A toolbox for modeling and optimization
in matlab,” in Proc. the CASCSD Conferance Taipei, Taiwan,
http://www.math.nus.edu.sg/ mattohkc/sdpt3.html 2004.
[12] K.C. Toh, M.J. Todd, and R.H. Tutuncu, “SDPT3-aMATLAB soft-
ware package for semidefinite programming,” Optimization Methods
and Software, 1999.
3697