
HAL Id: hal-03093861
https://hal.archives-ouvertes.fr/hal-03093861
Submitted on 19 Oct 2021
HAL is a multi-disciplinary open access
archive for the deposit and dissemination of sci-
entic research documents, whether they are pub-
lished or not. The documents may come from
teaching and research institutions in France or
abroad, or from public or private research centers.
L’archive ouverte pluridisciplinaire HAL, est
destinée au dépôt et à la diusion de documents
scientiques de niveau recherche, publiés ou non,
émanant des établissements d’enseignement et de
recherche français ou étrangers, des laboratoires
publics ou privés.
3D Numerical Simulation of the Var Consumable
Electrode Melting Process
Rayan Bhar, A. Jardy, P. Chapelle, Vincent Descotes
To cite this version:
Rayan Bhar, A. Jardy, P. Chapelle, Vincent Descotes. 3D Numerical Simulation of the Var Consum-
able Electrode Melting Process. Metallurgical and Materials Transactions B, Springer Verlag, 2020,
51 (6), pp.2492-2503. �10.1007/s11663-020-01966-x�. �hal-03093861�

1
3D NUMERICAL SIMULATION OF THE VAR CONSUMABLE
1
ELECTRODE MELTING PROCESS
2
3
R. Bhar
1,2
, A. Jardy
1
, P. Chapelle
1*
and V. Descotes
2
4
5
6
1
Institut Jean Lamour – UMR CNRS 7198, LabEx DAMAS, Université de Lorraine, 2 allée
7
André Guinier, Campus Artem, 54011 Nancy Cedex, France
8
2
Aperam Alloys Imphy – Avenue Jean Jaurès, BP-1, 58160 Imphy, France
9
10
*e-mail: pierre.chapelle@univ-lorraine.fr
11
12
Keywords: VAR process, consumable electrode, dripping, liquid metal film, melt rate
13
14
Abstract
15
16
A 3D numerical model was set-up to simulate the formation and dynamics of the liquid metal
17
film under the consumable electrode during VAR process. In the present paper the
18
implementation of this model is described. It was developed using the open source
19
computational fluid dynamics (CFD) software OpenFOAM. The model solves coupled
20
momentum and energy equations combined with a volume-of-fluid (VOF) method to track the
21
liquid metal free surface. The melting of the electrode material is modelled with an enthalpy-
22
porosity approach. The electric power supplied by the arc is supposed to be uniformly
23
distributed over the surface of the electrode tip. For a given electric arc power, the model
24
enable to quantitatively predict the dripping rate, hence the overall melt rate. Besides the
25
thermal behavior of the electrode, simulation results illustrate the dynamics of the liquid film
26
and the transfer mechanisms of the liquid metal during VAR melts performed with short and
27
long interelectrode gaps.
28
29
Nomenclature
30
Symbol
Description Unit
α
m
Metal volume fraction
[-]
β
Dilatation coefficient [K
-
1
]
γ
Solid volume fraction [-]
ε
Turbulent kinetic energy dissipation rate [ m
2
.s
-
3
]
λ
2
Secondary dendrite arm spacing [m]
µ
Dynamic viscosity [Pa.s
-
1
]
µ
t
Turbulent dynamic viscosity [Pa.s
-
1
]
ρ
Density [kg.m
-
3
]
σ
Surface tension [N.m
-
1
]
σ
ST
Stefan Boltzmann constant [W.m
-
2
.K
-
4
]
Cp
Specific heat [J.K
-
1
.kg
-
1
]
f
σ
Volumetric surface tension force [N.m
-
3
]
h
Total enthalpy [J.m
-
3
]
k
Turbulent kinetic energy [m². s
-
2
]

2
k
c
Curvature [m
-
1
]
k
Thermal conductivity [W.m
-
1
.K
-
1
]
k
t
Turbulent thermal conductivity [W.m
-
1
.K
-
1
]
L
Latent heat of melting [J.kg
-
1
]
P
arc
Power delivered by the arc to the electrode
P
rad
Power radiated from the electrode lateral wall
P
Pressure
T
Temperature [K]
T
sol
Solidus temperature [K]
T
liq
Liquidus temperature [K]
U
Velocity vector [m.s
-
1
]
m
Metal
VOF
Volume Of Fluid
CSF
Continuum Surface Force
CFL
Courant-Friedrich-Lewy
MULES
Multidimensional universal limiter with
explicit solution
31
32
I. Introduction
33
34
Vacuum arc remelting (VAR) is a secondary remelting process used to improve cleanliness
35
as well as chemical and mechanical homogeneity of metal ingots. VAR was the first remelting
36
process to be used commercially for superalloy processing. It is also typically the final stage
37
in the melting cycle of reactive metals such as titanium and zirconium alloys.
[1]
38
The process consists of melting a consumable electrode under vacuum (see Fig. 1). The
39
heat source is a DC electric arc of low voltage and high current. The arc is created between
40
the electrode (cathode) and the base plate of a water-cooled copper crucible at the beginning
41
of the melt, then between the electrode and the secondary ingot (anode) forming in the
42
crucible. The melting of the tip of the electrode generates a liquid metal film under the
43
electrode, from which metal drops are produced that fall under the action of gravity into the
44
crucible and progressively solidify to form the secondary ingot. At any instant, the ingot is
45
composed of three zones: the fully solidified metal, the liquid pool fed by metal drops and an
46
intermediate mushy zone.
47
48

3
49
Figure 1: Schematic representation of the vacuum arc remelting process.
50
The quality of the produced ingots strongly depends on the operating conditions of
51
remelting. Among them, the melt rate and the interelectrode gap play a key role, since they
52
have significant effects on heat transfer conditions at the free surface of the liquid pool, which
53
have important implications on the ingot structure and chemical homogeneity
[2]
.
54
The VAR process has been investigated previously with both experimental and numerical
55
approaches. On the experimental side, some studies were devoted to establish various
56
correlations between the operating parameters
[3,4]
, whereas some research work focused on
57
the electric arc behavior and metal transfer mechanisms in the interelectrode region, which
58
were observed using high speed video cameras in specifically instrumented VAR furnaces
59
[5,6]
. Modelling of the VAR process is a difficult task, because the process involves a wide
60
range of coupled complex physical and chemical phenomena, such as fluid flow, heat and
61
mass transfer, solidification (macro and microsegregation), electromagnetic forces… In the
62
literature, most modelling works deal with the development of Computational Fluid
63
Dynamics (CFD) models of the ingot growth and solidification. The majority of authors
64
considers a 2D axisymmetric geometry of the ingot and solves the conservation equations of
65
mass, momentum and energy, accounting for turbulence phenomena and electromagnetic
66
forces in the liquid pool as well as the solidification of the metal. Examples of such models
67
are the SOLAR code
[7]
and the MeltFlow-VAR code
[8]
. More recently, a multiscale 3D
68
numerical model of VAR was developed by Pericleous et al.
[9]
, which deals also with the
69
ingot behavior. Contrary to the ingot, the consumable electrode has received relatively little
70
attention, with very few modelling works reported, all restricted to thermal phenomena in the
71
electrode. Numerical studies on the formation and dynamics of the liquid film under the
72
electrode are in particular missing up to now. Bertram and Zanner
[10]
described a transient
73
and one-dimensional model of the heat transfer in the electrode, which was applied to study
74
the effect of the melting current and the gap length on the electrode melting. A similar model,
75
including an explicit account of radiative losses from the lateral walls of the electrode, was
76
presented by Jardy et al.
[11]
. Lately, a step forward was made by El Mir et al.
[12]
and Jardy et
77
al.
[13]
, who reported an unsteady model of heat transfer in the electrode, considering
78
respectively 2D and 3D geometries. Besides the electrode melt rate, these latter models enable
79
to predict, contrary to previous studies, the evolution of the shape of the electrode tip
80
throughout the melt.
81
82

4
The present work focuses on the interelectrode gap of the VAR process. The aim is to
83
numerically study the formation and deformation of the liquid film under the electrode and
84
the transfer mechanisms of the liquid metal in the interelectrode gap. A further objective is to
85
predict the melt rate of the electrode for a given electric arc power. For this purpose, a 3D
86
model describing the melting of the consumable electrode and the dynamics of the liquid film
87
formed at the electrode tip was developed using the CFD open source software OpenFOAM.
88
The model considers fuid flow under turbulent regime, heat transfer with phase change and
89
the deformation of the free surface of the liquid film. The model is concerned with both large
90
interelectrode gaps, for which the metal transfer results from the formation of molten metal
91
drops from the electrode and their detachment before contacting the ingot, and short
92
interelectrode gaps, for which the metal transfer involves the formation of intermittent molten
93
metal bridges (drip-shorts) between the electrode and the ingot. In section 2, the model is
94
described, including physical and mathematical issues, constitutive equations, boundary
95
conditions and the numerical procedure. In section 3, examples of model results detailing the
96
computed dynamics of the liquid film and thermal behavior of the electrode during the VAR
97
melt of a small-scale electrode and a fully-scale one are presented. Finally, conclusions of the
98
present study are drawn in section 4.
99
100
II. Numerical model
101
102
The formation and dynamics of the liquid film under the consumable electrode during the
103
VAR process is simulated with a multiphase CFD approach. The metal phase change is
104
accounted for using the enthalpy-porosity method
[14]
and the shape and position of the free
105
surface of the liquid film are calculated using the volume of fluid (VOF) interface capturing
106
method
[15]
.
107
108
The developed model is based on the following assumptions.
109
(1) The heat flux provided by the arc to the electrode is considered to be uniformly
110
distributed at the base of the electrode. The influence on the arc heat flux distribution of the
111
motion of individual cathode spots and of the possible existence of a relatively slow ensemble
112
motion of the arc (see e.g.
[16]
[17]
) is not examined in this study.
113
(2) As a first step towards a complete description of the liquid film behavior,
114
magnetohydrodynamic effects produced by the arc current (i.e. electromagnetic forces acting
115
on the liquid metal) are not taken into account.
116
(3) In a VAR furnace, the liquid metal film is exposed to a low pressure arc plasma. The
117
present model does not deal with the description of this complex latter phase, which is
118
represented here as a neutral gas phase.
119
(4) All thermophysical properties are considered to be independent of temperature and
120
identical in the solid and liquid phases. The metal density is made temperature dependent only
121
in the buoyancy term in the momentum equation.
122
(5) As explained later in section II.A, when computing the flow, a specific procedure was
123
introduced to eliminate non-physical spurious velocities generated near the interface in the
124
gas region. This procedure is applied at the end of each time step after calculating the flow in
125
both the liquid and gas regions. It is based on a simple filtering scheme designed to set to zero
126



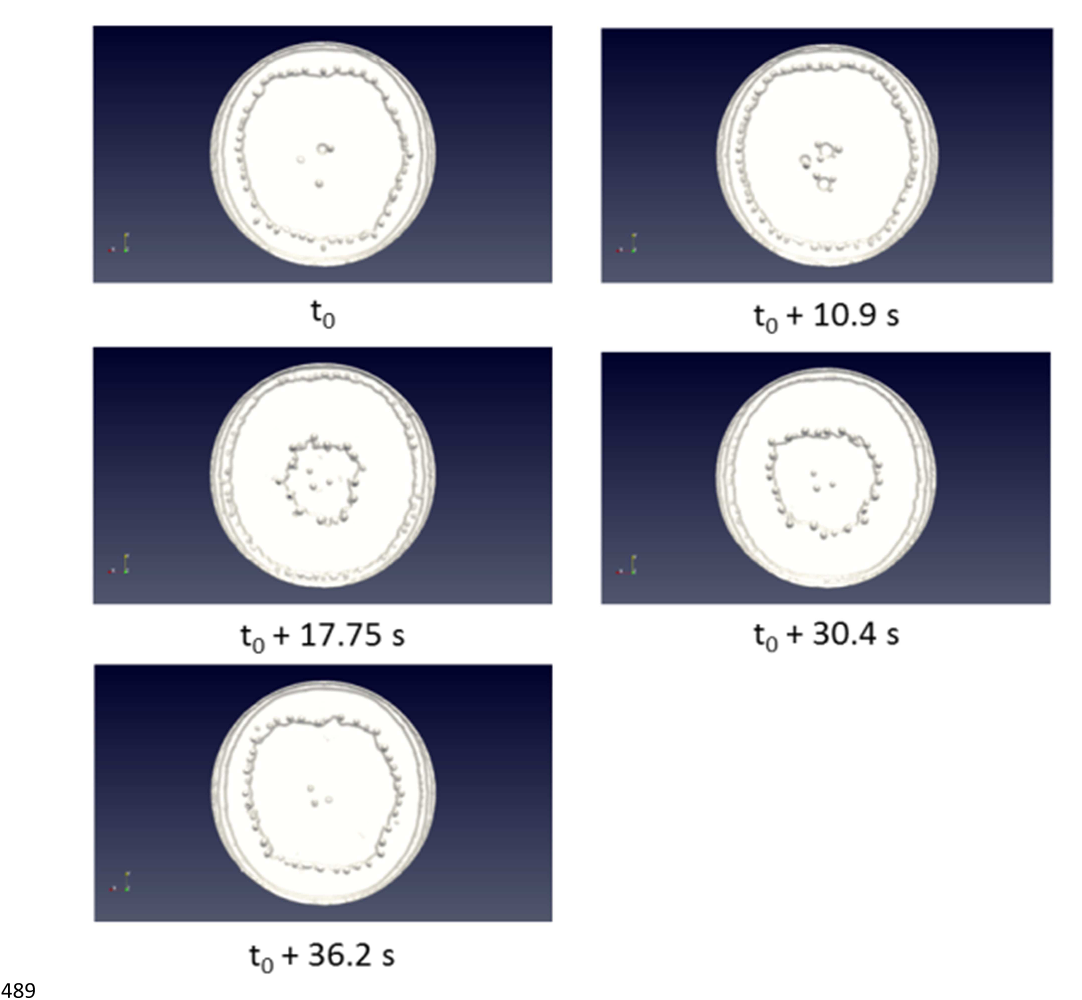

![Figure 5: Formation and detachment of a drop observed experimentally [6] (top row) 376 and predicted by the numerical model (bottom row). 377](/figures/figure-5-formation-and-detachment-of-a-drop-observed-3lqhxps8.png)




