3WaySym-Scal: Three-Way Symbolic
Multidimensional Scaling
P.J.F. Groenen
1
and S. Winsberg
2
1
Econometric Institute, Erasmus University Rotterdam,
P.O. Box 1738, 3000 DR Rotterdam, The Netherlands
email: groenen@few.eur.nl
2
Predisoft, San Pedro, Costa Rica
email: SuzanneWinsberg@predisoft.com
Econometric Institute Report EI 2006-49
Abstract. Multidimensional scaling aims at reconstructing dissimilarities between
pairs of objects by distances in a low dimensional space. However, in some cases the
dissimilarity itself is not known, but the range, or a histogram of the dissimilarities
is given. This type of data fall in the wider class of symbolic data (see Bock and
Diday (2000)). We model three-way two-mode data consisting of an interval of
dissimilarities for each object pair from each of K sources by a set of intervals of
the distances defined as the minimum and maximum distance between two sets
of embedded rectangles representing the objects. In this paper, we provide a new
algorithm called 3WaySym-Scal using iterative majorization, that is based on an
algorithm, I-Scal developed for the two-way case where the dissimilarities are given
by a range of values ie an interval (see Groenen et al. (2006)). The advantage of
iterative majorization is that each iteration is guaranteed to improve the solution
until no improvement is possible. We present the results on an empirical data set
on synthetic musical tones.
Keywords: Multidimensional scaling, Three-way data, Interval data, Sym-
bolic data analysis, 3WaySym-Scal.
1 Introduction
Classical multidimensional scaling (MDS) models the dissimilarities among a
set of objects as distances between points in a low dimensional space. The aim
of MDS is to represent and recover the relationships among the objects and to
reveal the dimensions giving rise to the space. To illustrate: the goal in many
MDS studies, for example, in psychoacoustics or marketing is to visualize
the objects and the distances among them and to discover and reveal the
dimensions underlying the dissimilarity ratings, that is, the most important
perceptual attributes of the objects.
Often, the proximity data available for the n objects consist of a single
numerical value for the dissimilarity δ
ij
between each object pair. Then, the

2 Patrick J.F. Groenen and Suzanne Winsberg
data may be presented in a single dissimilarity matrix with the entry for
the i-th row and the j-th column being a single numerical value represent-
ing the dissimilarity between the i-th and j-th object (with i = 1, . . . , n and
j = 1, . . . , n). Techniques for analyzing this two-way, one-mode data have
been developed (see, e.g., Kruskal (1964), Winsberg and Carroll (1989), or
Borg and Groenen (2005)). Sometimes proximity data are collected from K
sources, for example, a panel of K judges or under K different conditions,
yielding three-way two-mode data and an n×n× K array of single numerical
values. Techniques have been developed to deal with this form of data permit-
ting the study of individual or group differences underlying the dissimilarity
ratings (see, e.g., Carroll and Chang (1972), Winsberg and DeSoete (1993)).
All of these above mentioned MDS techniques require that each entry of
the dissimilarity matrix, or matrices be a single numerical value. However,
the objects in the set under consideration may be of such a complex nature
that the dissimilarity between each pair of them is better represented by a
range, that is, an interval of values, or a histogram of values rather than a
single value. For example, if the number of objects under study becomes very
large, it may be unreasonable to collect pairwise dissimilarities from each
judge and one may wish to aggregate the ratings from many judges where
each judge has rated the dissimilarities from a subset of all the pairs. Then,
rather than using an average value of dissimilarity for each object pair one
would wish to retain the information contained in the interval or histogram
of dissimilarities obtained for each pair of objects. Or, it might be useful to
collect data reflecting the imprecision or fuzziness of the dissimilarity between
each object pair. Then, the ij-th entry in the n × n data matrix, that is, the
dissimilarity between objects i and j, is either an interval or an empirical
distribution of values (a histogram). In these cases, the data matrix consists
of symbolic data.
By now, MDS of symbolic data can be analyzed by several techniques.
The case where the dissimilarity between each object pair is represented by
a range or interval of values has been treated by Denœux and Masson (2000)
and Masson and Denœux (2002). They model each object as alternatively a
hyperbox (hypercube) or a hypersphere in a low dimensional space and use
a gradient descent algorithm. Groenen et al. (2006) have developed an MDS
technique for interval data which yields a representation of the objects as
hyperboxes in a low-dimensional Euclidean space rather than hyperspheres
because the hyperbox representation is reflected as a conjunction of p prop-
erties where p is the dimensionality of the space. We shall follow this latter
approach here.
The hyperbox representation is interesting for two reasons. First a hyper-
box is more appealing because it allows a strict separation between the units
of the dimensions it uses. For example, the top speed of a certain type of car
might be between 170 and 190 km/h and its fuel consumption between 8 and
10 liters per 100 km. These aspects can be easily described alternatively as

3WaySym-Scal: Three-Way Symbolic Multidimensional Scaling 3
an average top speed of 180 km/h plus or minus 10 km/h and an average fuel
consumption of 9 liters per 100 km plus or minus 1. Both formulations are
in line with the hyperbox approach. However, the hypersphere interpretation
would be to state that the car is centered around a top speed of 180 km/h
and a fuel consumption of 9 liters per 100 km and give a radius. The units
of this radius cannot b e easily expressed anymore. A second reason for using
hyperboxes is that we would like to discover relationships in terms of the
underlying dimensions. The use of hyperboxes leads to unique dimensions,
whereas the the use of hyperspheres introduces the freedom of rotation so
that dimensions are not unique anymore.
Groenen and Winsberg (2006) have extended the method developed by
Groenen et al. (2006) to deal with the case in which the dissimilarity between
object i and object j is an empirical distribution of values or, equivalently, a
histogram.
All of the methods described above for MDS of symbolic data treat the
two-way one-mode case. That is, they deal with a single data matrix. Here, we
extend that approach to deal with the two-mode three-way case. We consider
the case where each of K judges denote the dissimilarity between the i-th and
j-th object pair as an interval, or a histogram thereby giving a range of values
or a fuzzy dissimilarity. So, the accent here will be on individual differences.
Of course, the method also applies to the case where data is collected for K
conditions, where for each condition the dissimilarity between the i-th and
j-th pair is an interval, or a histogram.
In the next section, we review briefly the I-Scal algorithm developed by
Groenen et al. (2006) for MDS of interval dissimilarities based on iterative
majorization. Then, we present an extension of the method to the three-way
two-mode case and analyze an empirical data sets dealing with dissimilar-
ities of sounds. The paper ends with some conclusions and suggestions for
continued research.
2 MDS of Interval Dissimilarities
We now review briefly the case of two-way one-mode MDS of interval dissim-
ilarities. In this case, an interval of a dissimilarity will be represented by a
range of distances between the two hyperboxes of objects i and j. This ob-
jective is achieved by representing the objects by rectangles and approximate
the upper bound of the dissimilarity by the maximum distance between the
rectangles and the lower bound by the minimum distance between the rect-
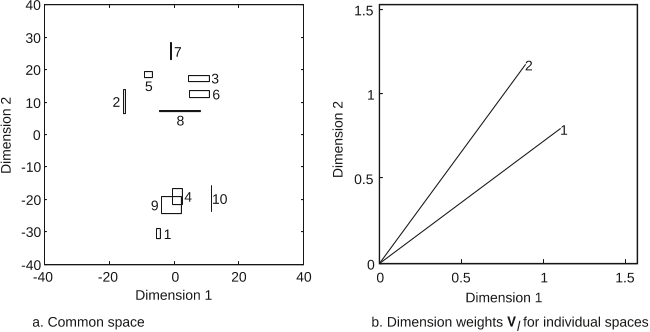
angles. An example of rectangle representation is shown in Figure 1. It also
indicates how the minimum and maximum distance b etween two rectangles
is defined.
By using hyperboxes, both the distances and the coordinates are ranges.
Let the coordinates of the centers of the rectangles be given by the rows of
the n × p matrix X, where n is the number of objects and p the dimen-

4 Patrick J.F. Groenen and Suzanne Winsberg
-0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
1
2
3
4
5
6
7
8
9
10
d
28
(L)
d
28
(U)
Fig. 1. Example of distances in MDS for interval dissimilarities where the objects
are represented by rectangles.
sionality. The distance from the center of rectangle i along axis s, denoted
by the spread, is represented by r
is
which is by definition nonnegative. The
maximum Euclidean distance between rectangles i and j is given by
d
(U)
ij
(X, R) =
Ã
p
X
s=1
[|x
is
− x
js
| + (r
is
+ r
js
)]
2
!
1/2
(1)
and the minimum Euclidean distance by
d
(L)
ij
(X, R) =
Ã
p
X
s=1
max[0, |x
is
− x
js
| − (r
is
+ r
js
)]
2
!
1/2
. (2)
This definition implies that rotation of the axes changes the distances be-
tween the hyperboxes because they are always parallel to the rotated axes.
This sensitivity for rotation can be seen as an asset because it makes a so-
lution rotational unique, which is not true for ordinary MDS. In the special
case of R = 0, the hyperboxes b ecome points and the rotational uniqueness
disappears as in ordinary MDS.
Symbolic MDS for interval dissimilarities aims at approximating the lower
and upper bounds of the dissimilarities by minimum and maximum distances
between rectangles. This objective is formalized by the I-Stress loss function
σ
2
I
(X, R) =
n
X
i<j
w
ij
h
δ
(U)
ij
− d
(U)
ij
(X, R)
i
2
+
n
X
i<j
w
ij
h
δ
(L)
ij
− d
(L)
ij
(X, R)
i
2
,
where δ
(U)
ij
is the upper bound of the dissimilarity of objects i and j, δ
(L)
ij
is
the lower bound , and w
ij
is a given nonnegative weight. σ
2
I
(X, R) can be
minimized by iterative majorization (see Groenen et al. (2006)).

3WaySym-Scal: Three-Way Symbolic Multidimensional Scaling 5
Iterative majorization has the advantage that I-Stress is guaranteed to
reduce in each iteration from any starting configuration until a stationary
point is obtained. In practice, the algorithm stops at a stationary point that
is a local minimum. Another important property for the purpose of this paper
is that, in each iteration, the algorithm operates on a quadratic function in X
and R. Groenen et al. (2006) have derived the quadratic majorizing function
for σ
2
I
(X, R) as the one at the right hand side of
σ
2
I
(X, R) ≤
p
X
s=1
(x
0
s
A
(1)
s
x
s
− 2x
0
s
B
(1)
s
y
s
)
+
p
X
s=1
(r
0
s
A
(2)
s
r
s
− 2r
0
s
b
(2)
s
) +
p
X
s=1
X
i<j
(γ
(1)
ijs
+ γ
(2)
ijs
), (3)
where x
s
is column s of X, r
s
is column s of R, y
s
is column s of Y (the pre-
vious estimate of X). The matrices A
(1)
s
, B
(1)
s
, A
(2)
s
, vectors b
(2)
s
, and scalars
γ
(1)
ijs
, γ
(2)
ijs
all depend dependent on previous estimates of X and R, hence
they are known at the present iteration. Their exact definition can be found
in Groenen et al. (2006). For our purposes, it is important to realize that the
majorizing function at the right of (3) is quadratic in X and R, so that an
update can be readily derived by setting the derivatives equal to zero.
Another important feature of the majorizing function being quadratic is
that it becomes easy to impose the constraints that we will need for the
extension to two-mode three-way symbolic MDS proposed in this paper. For
more details on iterative majorization and its use in three-way MDS, see, for
example, De Leeuw and Heiser (1980) and Borg and Groenen (2005).
3 Two-Mode Three-Way MDS of Interval Data
The I-Scal algorithm developed by Groenen et al. (2006) can be extended
quite easily to two-mode three-way interval data. In this case, we have an
interval available of the dissimilarities available for replication ` = 1, . . . , L.
Then, δ
(L)
ij`
and δ
(U)
ij`
are the lower and upper boundary of the interval of δ
ij
for
replication `. Of course, a normal I-Scal solution could be computed for every
replication separately. However, here we impose restrictions of the weighted
Euclidean model similar to the Indscal approach of Carroll and Chang (1972).
The main idea is to have a single common space of hyperboxes and allow
each replication ` to stretch or shrink the dimensions to fit its ranges of
dissimilarities as good as possible. Let X and R denote here the centers
and spreads of the hyperboxes in the common space. Then, the weighted
Euclidean model restrictions imply that the hyperboxes for the individual
replication ` are modelled as
X
`
= XV
`
(4)
R
`
= RV
`
, (5)