4k-point FFT algorithms based on optimized
twiddle factor multiplication for FPGAs
Fahad Qureshi, Syed Asad Alam and Oscar Gustafsson
Department of Electrical Engineering, Link
¨
oping University
SE-581 83 Link
¨
oping, Sweden
E-mail: {fahadq, asad, oscarg}@isy.liu.se
Abstract—In this paper, we propose higher point FFT (fast
Fourier transform) algorithms for a single delay feedback
pipelined FFT architecture considering the 4096-point FFT.
These algorithms are different from each other in terms of
twiddle factor multiplication. Twiddle factor multiplication com-
plexity comparison is presented when implemented on Field-
Programmable Gate Arrays(FPGAs) for all proposed algorithms.
We also discuss the design criteria of the twiddle factor multi-
plication. Finally it is shown that there is a trade-off between
twiddle factor memory complexity and switching activity in the
introduced algorithms.
I. INTRODUCTION
Computation of the discrete Fourier transform (DFT) and
inverse DFT is used in for e.g. orthogonal frequency-division
multiplexing (OFDM) communication systems, Digital Video
Broadcasting (DVB) and spectrometers. Few of these systems
require large point FFT, usually more than 1K point.
An N-point DFT can be expressed as
X(k)=
N−1
n=0
x (n) W
k
N
,k=0, 1,...,N − 1 (1)
where W
N
= e
−j
2π
N
is the twiddle factor, the N :th primitive
root of unity with its exponent being evaluated modulo N , n is
the time index, and k is the frequency index. Various methods
for efficiently computing (1) have been the subject of a large
body of published literature. They are commonly referred to as
fast Fourier transform (FFT) algorithms. Also, many different
architectures to efficiently map the FFT algorithm to hardware
have been proposed [1].
A commonly used architecture for transforms of length
N = b
r
is the pipelined FFT [2]. The pipeline architecture
is characterized by continuous processing of input data. In
addition, the pipeline architecture is highly regular, making
it straightforward to automatically generate FFTs of various
lengths. Especially for the large point FFT, reduces the com-
putational complexity as well as hardware complexity.
Figure 1 outlines the architecture of a Radix-2
i
single-path
delay feedback (SDF) decimation in frequency (DIF) pipeline
FFT architecture of length N =32. This architecture is
generic while the required ranges of each complex twiddle
factor multiplier is outlined in Table I for varying values of
i. For the twiddle factor multipliers with small ranges special
methods have been proposed. Especially, one can note that for
a W
4
multiplier the possible coefficients are {±1, ±j} and,
TABLE I
M
ULTIPLICATION RESOLUTION AT DIFFERENT STAGES FOR VARIOUS FFT
ALGORITHMS (N = 256).
Stage number
Radix 1 2 3 4 5 6 7
2 W
256
W
128
W
64
W
32
W
16
W
8
W
4
2
2
[3] W
4
W
256
W
4
W
64
W
4
W
16
W
4
2
3
[4] W
4
W
8
W
256
W
4
W
8
W
32
W
4
2
4
[5] W
4
W
8
W
16
W
256
W
4
W
8
W
16
2
5
[6] W
4
W
8
W
16
W
32
W
256
W
4
W
8
2
6
[6] W
4
W
8
W
16
W
32
W
64
W
256
W
4
hence, this can be simply solved by optionally interchanging
real and imaginary parts and possibly negate (or replace the
addition with a subtraction in the subsequent stage). In [5], [8]
twiddle factor multiplication for {W
8
,W
16
, and W
32
} using
constant multiplication were proposed. However, another way
to solve the twiddle factor multiplication is to use a general
complex multiplier and pre-compute the twiddle factors and
store them in a memory.
BF
BF
BF BF
116 248
BF
Stage 2Stage 1 Stage 3
Stage 4
Stage 5
WWWW
Fig. 1. Generalized Radix-2 single-path delay feedback (SDF) decimation
in frequency (DIF) pipeline FFT architecture (N =32) with twiddle factor
stages as used in Table I.
In digital CMOS circuits, dynamic power is the dominating
part of the total power consumption which can be approxi-
mated by [9]
P
dyn
=
1
2
V
2
DD
f
c
C
L
α (2)
where V
DD
is the supply voltage, f
C
is the clock frequency,
C
L
is the load capacitance and α is the switching activity. Low
complexity and low power architecture designs are always
desirable. Low power can be achieved by either reducing
the switching activity or resource utilization. In [10]–[13],
methods for reducing the size of the coefficient memory has

been proposed. In [7], the authors proposed balanced binary
tree decomposition and claim optimal twiddle factor memory
requirement.
In this work we propose algorithms to implement the 4096-
point FFT. Butterfly structure of these proposed architectures
are same but twiddle factor multiplications are different. Also
discussed are the design criteria for the proposed algorithms on
the basis of implementation of twiddle factor multiplication.
The rest of the paper is organized as follows. Next sec-
tion describes the binary tree representation of Cooley-Tukey
algorithm. In Section III we discuss the design criteria of
the algorithms. In Section IV we introduce the proposed
architectures derived from radix-2
i
then in Section V, some
results are presented. Finally, some conclusions are presented.
II. B
INAY TREE REPRESENTATION OF COOLEY-TUKEY
ALGORITHM
The Cooley-Tukey FFT algorithm can be expressed as
X [Qk
1
+ k
2
]
=
P −1
n
1
=0
Q−1
n
2
=0
x [n
1
+ Pn
2
] W
n
2
k
2
Q
W
n
1
k
2
M
W
n
1
k
1
P
0 ≤ n
1
,k
1
≤ P − 1; 0 ≤ n
2
,k
2
≤ Q − 1 (3)
Where, N, P and Q are considered to be powers of 2,
i.e., N =2
p+q
, P =2
p
and Q =2
q
where p and q are
positive integers. Here, the N -point DFT is decomposed into
the QP-point and PQ-point DFTs. These are named as inner
DFTs and outer DFTs repectively. Between these DFTs we
have twiddle factor multiplications. Typically, the P and Q-
point DFTs are again divided into smaller DFTs. An efficient
representation of algorithms of this type is the binary tree
representation [7]. An example of a binary tree is shown in
Fig. 2 corresponding to (3). The left branch corresponds to the
P =2
p
-point DFT and the right branch to the Q =2
q
-point
DFT. The resolution of the interconnecting twiddle factor is
N =2
p+q
, i.e., a W
N
multiplier is required.
p+q
p
q
Fig. 2. Illustration of binary tree corresponding to (3).
FFT algorithm is categorized by the way Cooley-Tukey re-
cursive decomposition is applied. These decompositions finally
reach butterfly operations which greatly influences the FFT
architecture. A small radix is more desirable because it has a
simple butterfly operation but higher radix has less number
of twiddle factor multiplications. The radix-2
i
has simple
radix-2 butterfly operations and twiddle factor multiplications
depend upon the value of i. The generalized radix-2(N = 32)
W
3,25
x(16)
x(17)
x(18)
x(19)
x(20)
x(21)
x(22)
x(23)
x(24)
x(25)
x(26)
x(27)
x(28)
x(29)
x(30)
x(31)
x(0)
x(2)
x(3)
x(4)
x(5)
x(6)
x(7)
x(8)
x(9)
x(10)
x(11)
x(12)
x(13)
x(14)
x(15)
x(1)
W
0,25
W
0,27
x(1)
x(17)
x(9)
x(5)
x(13)
x(29)
x(3)
x(19)
x(11)
x(27)
x(7)
x(23)
x(15)
x(31)
x(0)
x(8)
x(4)
x(28)
x(2)
x(10)
x(26)
x(6)
x(22)
x(14)
x(30)
x(20)
x(12)
x(16)
x(24)
x(18)
x(25)
x(21)
W
1,31
W
1,30
W
1,29
W
1,28
W
1,27
W
1,26
W
1,25
W
1,24
W
1,23
W
1,22
W
1,21
W
1,20
W
1,19
W
1,0
W
1,1
W
1,2
W
0,0
W
0,1
W
0,2
W
0,3
W
0,4
W
0,5
W
0,6
W
0,7
W
0,8
W
0,9
W
0,10
W
0,11
W
0,12
W
0,13
W
0,14
W
0,15
W
0,16
W
0,17
W
0,18
W
0,19
W
0,20
W
0,21
W
0,22
W
0,23
W
0,24
W
0,26
W
0,28
W
0,29
W
0,30
W
0,31
W
1,4
W
1,3
W
1,5
W
1,6
W
1
,7
W
1,8
W
1,9
W
1,10
W
1,11
W
1,12
W
1,13
W
1,14
W
1,15
W
1,16
W
1,17
W
1,18
W
2,0
W
2,1
W
2,2
W
2,3
W
2,4
W
2,5
W
2,6
W
2,7
W
2,8
W
2,9
W
2,10
W
2,11
W
2,12
W
2,
13
W
2,14
W
2,15
W
2,16
W
2,17
W
2,18
W
2,19
W
2,20
W
2,21
W
2,22
W
2,23
W
2,24
W
2,25
W
2,26
W
2,27
W
2,28
W
2,29
W
2,30
W
2,31
W
3,31
W
3,30
W
3,29
W
3,28
W
3,27
W
3,26
W
3,24
W
3,23
W
3,22
W
3,21
W
3,20
W
3,19
W
3,18
W
3,17
W
3,16
W
3,15
W
3,14
W
3,13
W
3,10
W
3,9
W
3,8
W
3,7
W
3,6
W
3,5
W
3,4
W
3,3
W
3,2
W
3,1
W
3,0
W
3,11
W
3,12
Fig. 3. Generalized Radix-2 32-point FFT signal flow graph
signal flow graph is shown in Fig. 3. Multiplication after
each butterfly operation is shown with row and column. The
radix-2
i
algorithm can be achieved by applying the balanced
decomposition for small point FFT.
III. C
RITERIA FOR ALGORITHM SELECTION
Algorithm selection criteria is the most important step to
design low power FFT algorithm. Twiddle factor multipli-
cation is one of the major power contributors of the single
delay feedback pipelined FFT architecture. Twiddle factor
multiplication requires both memory and complex multiplier
which consumes more power and more area.
A. Complexity of W
N
Multiplier
The simplest approach, is to just use a large look-up table to
store the twiddle factors. For a W
N
multiplier, N words need
to be stored. Twiddle factor multiplication is implemented with
one complex multiplier and LUTs to store the precomputed
coefficient. It should also be noted that this scheme possibly
stores the same twiddle factor in several positions as the
mapping is from row to twiddle factor and for radix-2
i
algorithms some twiddle factors appears more than once for
i ≥ 2. The complexity of the LUTs is depending upon the
size of the FFT and resolution of the twiddle factor. It also to
uses the well known octave symmetry to only store twiddle
factors for 0 ≤ α ≤ π/4 with an additional cost of address
mapping circuit [13].
The lower resolution N ≤ 16, complex multiplier can be
implemented with dedicated constant multiplier [5], [8].
1) W
8
Multiplier: A W
8
-multiplier only requires multipli-
cation by either 1 or sin
π
4
(cos
π
4
). This can easily be realized
using a multiplexer selecting between the input or the output

V
6
5
1
2
4
66
3
3
III
I
6
4
2
IV
II
6
5
1
Fig. 4. Decomposed algorithms for 64-point
of a constant multiplier with coefficient sin
π
4
. The constant
multiplier can be realized using a minimum number of adders
using the method in [14].
2) W
16
Multiplier: A W
16
-multiplier is a low resolution
multiplier. This twiddle factor multiplication can be imple-
mented with the dedicated constant multiplier of sin
π
8
, cos
π
8
and sin
π
4
with some control logic. [5] proposed a W
16
multiplier based on trigonometric identities which were im-
plemented with the constant coefficients sin
π
8
and cos
π
8
.In
[15] authors proposed the low complexity in terms of adder
with minimum error based on aware quantization method. In
the proposed architectures we implement dedicated constant
multiplier for W
16
twiddle factor multiplication.
B. Switching activity
Switching activity between two successive coefficients fed
to the complex multiplier affects the power consumption.
The coefficient reordering technique was proposed [16] to
design low power architecture. Algorithmic level changes
also affect the switching activity, depending upon how the
FFT decomposition is recursively applied to form a small
point FFT. In [17] the equivalent radix-2
2
algorithm with low
switching activity was proposed. In the proposed architecture,
we discuss switching activity of W
64
multiplication. The
different decompositions of the 64-point FFT block is shown
in Fig. 4 and the switching activity is tabulated in Table II. The
position of the twiddle factor is affecting the switching activity.
In case II and IV, we have same twiddle factor complexity
but case II has less switching activity. Switching activity also
depends upon whether any particular twiddle factor is located
on left or right branch of the tree. It is shown that there is a
trade off between complex multiplier and switching activity,
both having affect on power consumption.
TABLE II
S
WITCHING ACTIVITY OF DECOMPOSED W
64
MULTIPLICATION (12-BITS)
Twiddle factor I II III IV V
W
64
301 479 665 587 733
IV. PROPOSED ARCHITECTURES BASED ON RADIX-2
i
Considering the 4096-point FFT, based on the radix-2
i
decomposition the proposed algorithms are shown in Fig. 5(b-
d) with binary tree diagram. Each node corresponds to twiddle
factor multiplication. Twiddle factors are indexed by n and k,
the linear index map equations and sequences of required n
and k to determine the index. Proposed architectures can be
111
1
4
22
111
4
22
1
111
11
11
(a)
12
6
6
(c)
(b)
2
2
(d)
34
22
1
111
12
5
7
3
3
3
3
3
1
1
2
1
1
1
2
1
2
6
6
1
1
1
1
12
2
1
1
2
12
4
8
4
2
1
111
2
4
22
1
111
22
1
111
2
2
1
11
11
2
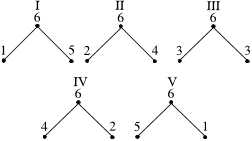
Fig. 5. (a) Balanced binary tree decomposition [7] (b-d) Proposed algorithms.
formulated with eq. 3. Here we formulated the first decompo-
sition of Fig. 5(a) expressed as
X [64k
1
+ k
2
]
=
64−1
n
1
=0
64−1
n
2
=0
x [n
1
+64n
2
] W
n
2
k
2
64
W
n
1
k
2
4096
W
n
1
k
1
64
(4)
where W
4096
is the twiddle factor multiplication which con-
nects the two decomposed DFTs. Similarly, we can apply
the decomposition equation on each node of the binary tree
representation of FFT. The generalized index mapping is
presented for all stages of any radix-2
i
algorithm [18]. Twiddle
factors of each algorithm with resolution are tabulated in
Table III.
V. R
ESULTS
We have analyzed the complexity and switching activity
of twiddle factor multiplications. Both these factors influence
low power designs. The architectures of the twiddle factor
multiplication have been coded in VHDL. In higher resolution
twiddle factor multiplication, we considered the LUTs to
store the precomputed twiddle factors with complex multiplier
and for others dedicated constant multiplier is considered
for multiplication. The twiddle factor memory and complex
multipliers were synthesized, targeting Virtex-4 FPGA. The
twiddle factors are represented using 12 bits each for real and
imaginary parts, using two’s complement representation. The
resulting complexity for each stage is illustrated in Table V.
The switching activity between successive coefficient fed
to the complex multiplier is defined in terms of Hamming
distance for each coefficient transition. The Hamming distance
is defined as the number of 1’s of the XOR operation between
two successive binary coefficient. Twiddle factors can be pre-
computed and stored in look-up tables instead of calculating
in real time. In pipelined SDF architecture, in each cycle
these stored coefficients are fed to the complex multiplier. The
sequence of the stored coefficients affect the switching activity.
The reading sequence is then simulated to obtain the resulting
switching activity. The results for the different algorithms are
shown in Table IV. The analysis of these results show that,
we have more options to implement 4096-point FFT.

TABLE III
M
ULTIPLICATION RESOLUTION AT DIFFERENT STAGES FOR BALANCED BINARY TREE DECOMPOSITION AND PROPOSED ALGORITHMS.
Stage number
Case 1 2 3 4 5 6 7 8 9 10 11
Balanced binary tree decomposition [7] W
4
W
8
W
64
W
4
W
8
W
4094
W
4
W
8
W
64
W
4
W
8
Proposed 1
st
W
4
W
16
W
4
W
256
W
4
W
16
W
4
W
4096
W
4
W
16
W
4
Proposed 2
nd
W
4
W
64
W
4
W
16
W
4
W
4096
W
4
W
64
W
4
W
16
W
4
Proposed 3
rd
W
4
W
16
W
4
W
128
W
4
W
8
W
4096
W
4
W
8
W
32
W
4
The first proposed architecture requires 2 complex multi-
plier while other architectures need 3 complex multipliers. The
hardware complexity of dedicated multiplier and the twiddle
factor memory is higher than others with less switching
activity. In the proposed architectures the complexity of the
dedicated constant multipliers and twiddle factor memory is
decreasing while switching activity is increasing from first to
third proposed architecture.
Low power design is trade off between these parameters.
In the proposed architectures we have better options to select
low power design than balanced binary tree algorithms.
TABLE IV
T
WIDDLE FACTOR MULTIPLICATION COMPLEXITY
Number of 4-input LUTs
Twiddle Balanced binary Proposed Algorithms
factor
decomposition [7] 1
st
2
nd
3
rd
W
8
4*215 – – 2*215
W
16
– 419*3 419*2 419
W
32
– – – 48
W
64
136+430 – 126+401 –
W
128
– – – 136
W
256
– 575 – –
W
4096
5967 6058 5967 6102
Total 7393 7890 7332 7135
Complex multiplier 3 2 3 3
TABLE V
S
WITCHING ACTIVITY OF TWIDDLE FACTOR
Twiddle Balanced binary Proposed Algorithms
factor
decomposition [7] 1
st
2
nd
3
rd
W
32
– – – 40437
W
64
587+38639 – 479+31475 –
W
128
– – – 1310
W
256
– 2388 – –
W
4096
34061 40726 34061 37481
Total 73287 43114 66015 79228
VI. CONCLUSIONS
In this work, we proposed the different algorithms for single
delay feedback architecture for higher radix, considering the
4096-point FFT. The twiddle factor multiplications at each
stage is different for each proposed algorithms. Low power
designs of each algorithm depends upon few twiddle factor
multiplication design parameters. Design criteria of twiddle
factor multiplication is trade off between these parameters.
It is shown that in the proposed algorithms we have better
choices to select the low power architecture for 4096-point
FFT.
R
EFERENCES
[1] L. Wanhammar, DSP Integrated Circuits, Academic Press, 1999.
[2] E. H. Wold and A. M. Despain, “Pipeline and parallel-pipeline FFT
processors for VLSI implementations,” IEEE Trans. Comp., vol. 33,
no. 5, pp. 414–426, May 1984.
[3] S. He and M. Torkelson, “A new approach to pipeline FFT processor,”
in Proc. IEEE Parallel Processing Symp., 1996, pp. 766–770.
[4] S. He and M. Torkelson, “Designing pipeline FFT processor for
OFDM(de)Modulation,” in Proc. IEEE URSI Int. Symp. Sig. Elect.,
1998, pp. 257–262.
[5] J.-E. Oh,and M.-S. Lim, “New radix-2 to the 4th power pipeline FFT
processor,” IEICE Trans. Electron., vol. E88-C, no. 8, pp. 694–697, Aug.
2005.
[6] A. Cortes, I. Velez and J. F. Sevillano,“Radix r
k
FFTs: matricial
representation and SDC/SDF pipeline implementation,” IEEE Trans. on
Signal Processing, vol. 57, no. 7, pp. 2824–2839, July 2009.
[7] Hyun-Yong Lee, and In-Cheol Park,“Balanced binary-tree decompo-
sition for area-efficient pipelined FFT processing,” IEEE Trans. on
Circuits and Systems-I, vol. 54, no. 4, pp. 889–900, April 2009.
[8] F. Qureshi and O. Gustafsson, “Low-complexity reconfigurable complex
constant multiplication for FFTs,” in Proc. IEEE Int. Symp. Circuits
Syst., Taipei, Taiwan, May 24–27, 2009.
[9] K. Johansson, O. Gustafsson, and L. Wanhammar, “Switching activity
estimation for shift-and-add based constant multipliers,” in Proc. IEEE
Int. Symp. Circuits Syst., Seattle, WA, USA, May. 18-21, 2008.
[10] Seungbeom Lee, Duk-bai Kim and Sin-Chong Park, “Power-efficient
design of memory based FFT processor with new addressing scheme,”
in Proc. Int. Symp. Communications and Information Technology, 26–29
Oct. 2004, pp. 678–681.
[11] F. Qureshi and O. Gustafsson, “Analysis of twiddle factor memory
complexity of radix-2
i
pipelined FFTs,” in Proc. Asilomar Conf. Signals
Syst. Comp., Pacific Grove, CA, Nov. 1-4, 2009.
[12] H. Cho, M. Kim, D. Kim, and J. Kim “R2
2
SDF FFT implementation
with coefficient memory reduction scheme,” in Proc. Vehicular Technol-
ogy Conf., 2006.
[13] M. Hasan and T. Arslan, “Scheme for reducing size of coefficient
memory in FFT processor,” Electronics Letters, vol. 38, no. 4, pp. 163–
164, Feb. 2007.
[14] O. Gustafsson, A. G. Dempster, K. Johansson, M. D. Macleod, and
L. Wanhammar, “Simplified design of constant coefficient multipliers,”
Circuits, Systems and Signal Processing, vol. 25, no. 2, pp. 225–251,
Apr. 2006.
[15] O. Gustafsson and F. Qureshi, “Addition aware quantization for low
complexity and high precision constant multiplication,” IEEE Signal
Processing Letters., vol. 17, no. 2, pp. 173-176, Feb. 2010.
[16] J. Ming Wu and Y. Chun Fan, “Coefficient ordering based pipelined
FFT/IFFT with minimum switching activity for low power WiMAX
communication system,” in Proc. IEEE Tenth Int. Symp. Consumer
Electronics, 2006, pp. 1–4.
[17] F. Qureshi and O. Gustafsson, “Twiddle factor memory switching
activity analysis of Radix-2
2
and equivalent FFT algorithms,” in Proc.
IEEE Int. Symp. Circuits Syst., Paris, France, 2010.
[18] F. Qureshi and O. Gustafsson, “Genralized twiddle factor index-Mapping
of radix-2 FFT algorithm,” in preparation.

![Fig. 5. (a) Balanced binary tree decomposition [7] (b-d) Proposed algorithms.](/figures/fig-5-a-balanced-binary-tree-decomposition-7-b-d-proposed-1pxd9q91.png)