MX Cohen Morlet wavelet definition 3 of 14
Overview of methods for time-frequency analysis
There are several time-frequency analysis methods, most of which produce qualitatively or
quantitatively similar results (Bruns 2004; Cohen 2014) . The three most commonly used are the
short-time fast Fourier transform, complex wavelet convolution, and filter-Hilbert. These three
methods have in common that they involve isolating a narrow temporal window of data and then
extracting its frequency spectrum.
A key parameter in time-frequency analysis is the one that governs the trade-off between temporal
precision and spectral precision; it is not possible to have simultaneously arbitrarily good precision in
both time and in frequency. Furthermore, the resulting smoothness is often advantageous for
averaging data across stimulus repetitions and individuals; thus, arbitrarily good precision can be
detrimental in applied data analysis of biological systems.
The key argument of this paper is that this crucial parameter is created and reported in a way that
obscures both the signal-processing and the theoretical assumptions that are imposed on the data,
and that shape the results. The key upshot of this paper is two alternative methods for creating and
reporting Morlet wavelets in a way that makes this key parameter transparent and easily
interpretable.
Advantages and assumptions of Morlet wavelets for time-frequency analysis
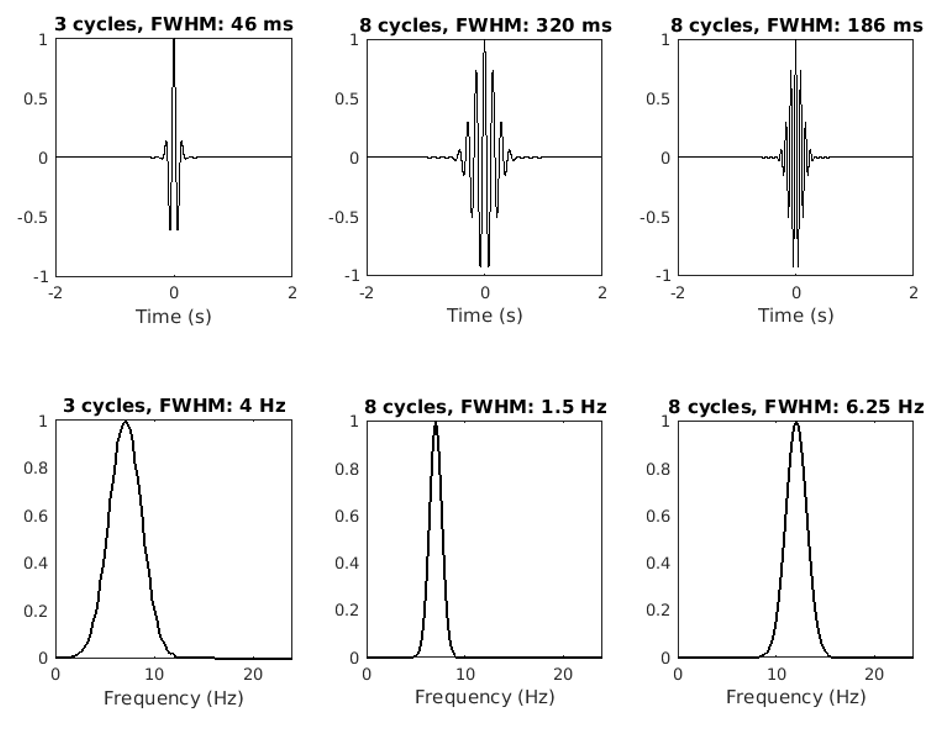
A Morlet wavelet is defined as a sine wave tapered by a Gaussian (Figure 2, top row). For
time-frequency analysis, a complex Morlet wavelet is used, in which the Gaussian tapers a complex
sine wave. The complex Morlet wavelet is then convolved with the time series signal, and the result
of convolution is a complex-valued signal from which instantaneous power and phase can be
extracted at each time point. Wavelet convolution can be conceptualized as a “template-matching”
procedure, in which each time point in the signal is compared against a template (the
Gaussian-windowed sine wave), and the result of the convolution is a time series of “similarities”
between the signal and the wavelet.
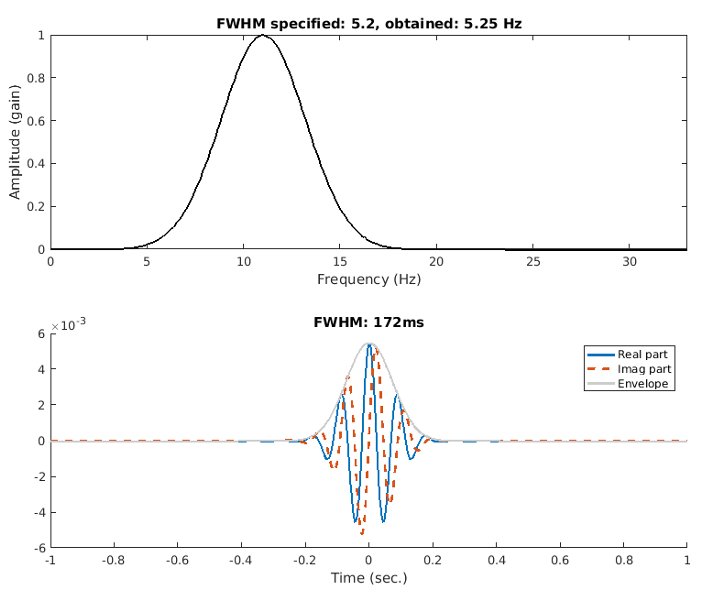
The tapering Gaussian has one parameter that defines its width (also called its shape or deviation). A
wider Gaussian leads to decreased temporal precision but increased spectral precision, and
vice-versa for a narrower Gaussian. This parameter is typically defined as the “number of cycles,” but
the purpose of this paper is to argue that it would be better to define the Gaussian width as the
full-width at half-maximum (FWHM), which is the distance in time between 50% gain before the peak
to 50% gain after the peak.
There are several advantages of Morlet wavelets for time-frequency analysis. One is that the Morlet
wavelet is Gaussian-shaped in the frequency domain (Figure 2, bottom row). The absence of sharp
edges minimizes ripple effects that can be misinterpreted as oscillations (this is a potential danger
associated with plateau-shaped filters). Second, the results of Morlet wavelet convolution retain the
temporal resolution of the original signal. Third, wavelet convolution is more computationally
efficient and requires less code compared to other methods, because it involves the smallest number
of computations, most of which are implemented using the fast Fourier transform.
.CC-BY-NC-ND 4.0 International licenseavailable under a
not certified by peer review) is the author/funder, who has granted bioRxiv a license to display the preprint in perpetuity. It is made