MX Cohen Morlet wavelet definition 1 of 14
A better way to define and describe Morlet wavelets
for time-frequency analysis
Michael X Cohen
Radboud University and Radboud University Medical Center; Donders Institute for Neuroscience
Correspondence: mikexcohen@gmail.com
Funding: MXC is funded by an ERC-StG 638589
Abstract
Morlet wavelets are frequently used for time-frequency analysis of non-stationary time series data,
such as neuroelectrical signals recorded from the brain. The crucial parameter of Morlet wavelets is
the width of the Gaussian that tapers the sine wave. This width parameter controls the trade-off
between temporal precision and frequency precision. It is typically defined as the “number of cycles,”
but this parameter is opaque, and often leads to uncertainty and suboptimal analysis choices, as well
as being difficult to interpret and evaluate. The purpose of this paper is to present alternative
formulations of Morlet wavelets in time and in frequency that allow parameterizing the wavelets
directly in terms of the desired temporal and spectral smoothing (as full-width at half-maximum).
This formulation provides clarity on an important data analysis parameter, and should facilitate
proper analyses, reporting, and interpretation of results. MATLAB code is provided.
.CC-BY-NC-ND 4.0 International licenseavailable under a
not certified by peer review) is the author/funder, who has granted bioRxiv a license to display the preprint in perpetuity. It is made
The copyright holder for this preprint (which wasthis version posted August 21, 2018. ; https://doi.org/10.1101/397182doi: bioRxiv preprint

MX Cohen Morlet wavelet definition 2 of 14
Motivation for time-frequency analysis
Many biological and physical systems exhibit rhythmic processes. Rhythmic temporal structure
embedded in time series data can be extracted and quantified using the Fourier transform or other
spectral analysis methods.
However, the Fourier transform has a “soft assumption” of signal stationarity, which means that the
spectral and other features of the signal remain constant over time. To be sure, the Fourier transform
is a perfect representation of the time series, regardless of its temporal dynamics. However, the
power spectrum resulting from the Fourier transform is easily visually interpretable only for
stationary signals; non-stationarities are encoded in the phase spectrum, which is typically
impossible to interpret visually.
Signal non-stationarities are the primary motivation for time-frequency analyses, in which the power
spectrum is computed over short windows of time. The primary assumption here is that the signal is
roughly stationary over some shorter (sliding) time window. For neural time series data, this
assumption is typically a few hundreds of milliseconds. An example of a “static” and “dynamic”
spectral representation of a non-stationary signal is presented in Figure 1.
Figure 1 . In the presence of signal non-stationarities (panel A), the “static” power spectrum from the
Fourier transform can be difficult to interpret (panel B). In these cases, a time-frequency analysis
(panel C) is often insightful.
.CC-BY-NC-ND 4.0 International licenseavailable under a
not certified by peer review) is the author/funder, who has granted bioRxiv a license to display the preprint in perpetuity. It is made
The copyright holder for this preprint (which wasthis version posted August 21, 2018. ; https://doi.org/10.1101/397182doi: bioRxiv preprint

MX Cohen Morlet wavelet definition 3 of 14
Overview of methods for time-frequency analysis
There are several time-frequency analysis methods, most of which produce qualitatively or
quantitatively similar results (Bruns 2004; Cohen 2014) . The three most commonly used are the
short-time fast Fourier transform, complex wavelet convolution, and filter-Hilbert. These three
methods have in common that they involve isolating a narrow temporal window of data and then
extracting its frequency spectrum.
A key parameter in time-frequency analysis is the one that governs the trade-off between temporal
precision and spectral precision; it is not possible to have simultaneously arbitrarily good precision in
both time and in frequency. Furthermore, the resulting smoothness is often advantageous for
averaging data across stimulus repetitions and individuals; thus, arbitrarily good precision can be
detrimental in applied data analysis of biological systems.
The key argument of this paper is that this crucial parameter is created and reported in a way that
obscures both the signal-processing and the theoretical assumptions that are imposed on the data,
and that shape the results. The key upshot of this paper is two alternative methods for creating and
reporting Morlet wavelets in a way that makes this key parameter transparent and easily
interpretable.
Advantages and assumptions of Morlet wavelets for time-frequency analysis
A Morlet wavelet is defined as a sine wave tapered by a Gaussian (Figure 2, top row). For
time-frequency analysis, a complex Morlet wavelet is used, in which the Gaussian tapers a complex
sine wave. The complex Morlet wavelet is then convolved with the time series signal, and the result
of convolution is a complex-valued signal from which instantaneous power and phase can be
extracted at each time point. Wavelet convolution can be conceptualized as a “template-matching”
procedure, in which each time point in the signal is compared against a template (the
Gaussian-windowed sine wave), and the result of the convolution is a time series of “similarities”
between the signal and the wavelet.
The tapering Gaussian has one parameter that defines its width (also called its shape or deviation). A
wider Gaussian leads to decreased temporal precision but increased spectral precision, and
vice-versa for a narrower Gaussian. This parameter is typically defined as the “number of cycles,” but
the purpose of this paper is to argue that it would be better to define the Gaussian width as the
full-width at half-maximum (FWHM), which is the distance in time between 50% gain before the peak
to 50% gain after the peak.
There are several advantages of Morlet wavelets for time-frequency analysis. One is that the Morlet
wavelet is Gaussian-shaped in the frequency domain (Figure 2, bottom row). The absence of sharp
edges minimizes ripple effects that can be misinterpreted as oscillations (this is a potential danger
associated with plateau-shaped filters). Second, the results of Morlet wavelet convolution retain the
temporal resolution of the original signal. Third, wavelet convolution is more computationally
efficient and requires less code compared to other methods, because it involves the smallest number
of computations, most of which are implemented using the fast Fourier transform.
.CC-BY-NC-ND 4.0 International licenseavailable under a
not certified by peer review) is the author/funder, who has granted bioRxiv a license to display the preprint in perpetuity. It is made
The copyright holder for this preprint (which wasthis version posted August 21, 2018. ; https://doi.org/10.1101/397182doi: bioRxiv preprint

MX Cohen Morlet wavelet definition 4 of 14
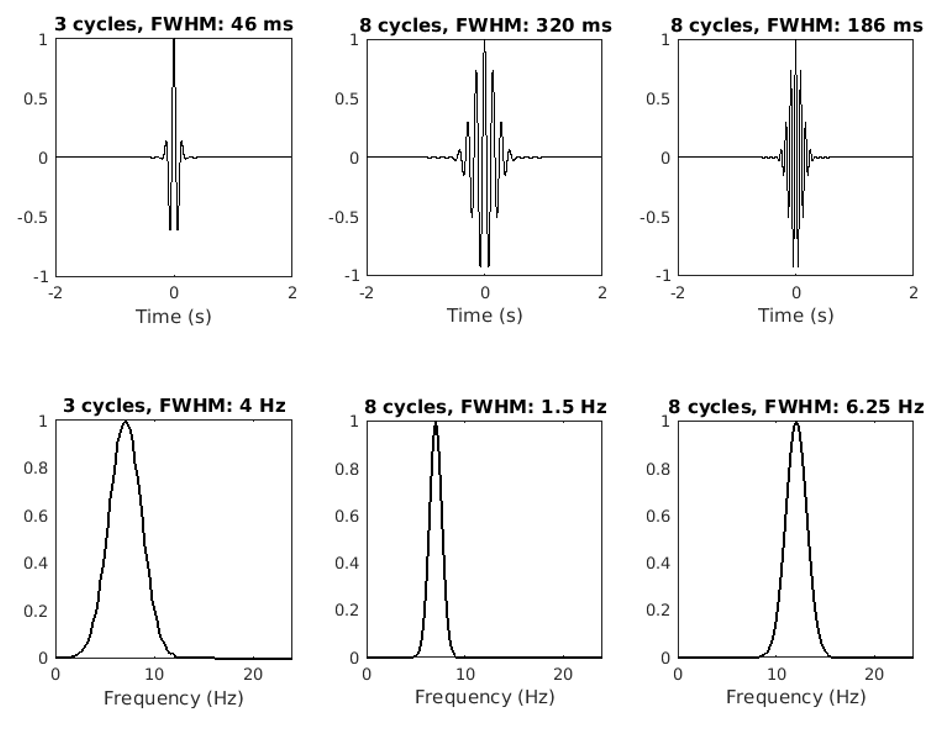
Figure 2 . Three Morlet wavelets in the time domain (upper row) and in the frequency domain (lower
row) with two frequencies and different time-frequency trade-off parameters. The argument of this
paper is that reporting this parameter in terms of full-width at half-maximum (FWHM) in the time
and/or frequency domains is more informative than number of cycles.
There are two key assumptions of Morlet wavelet-based time-frequency analysis. The first is that the
signal is roughly sinusoidal. Some researchers have noted that brain oscillations are probably not
shaped like pure sine waves (Cole and Voytek 2017; Jones 2016) . On the other hand, the
overwhelming success and ubiquity of time-frequency analysis methods indicates that minor
violations of this assumption are not deleterious for practical data analysis, hypothesis-testing, data
mining, and feature discovery. The sinusoidal assumption is therefore considered valid, and
additional detailed waveform analyses can be insightful in specific instances.
The second assumption of Morlet wavelet analysis concerns stationarity of the signal. Interpreting
the results of Morlet wavelet convolution relies on the assumption that the signal is stationary within
the time window that the wavelet has non-zero energy. Generally, this can be taken as the FWHM of
the Gaussian that is used to create the Morlet wavelet. Any signal non-stationarities that are smaller
than this FWHM will produce results that are difficult to interpret (similar to the “static” power
spectrum in Figure 1).
Appropriate selection of the width of the wavelet is a combination of signal processing
considerations, and theoretical/speculative considerations of the system from which the signal was
measured. This parameter is therefore important for time frequency data analysis, and yet is often
.CC-BY-NC-ND 4.0 International licenseavailable under a
not certified by peer review) is the author/funder, who has granted bioRxiv a license to display the preprint in perpetuity. It is made
The copyright holder for this preprint (which wasthis version posted August 21, 2018. ; https://doi.org/10.1101/397182doi: bioRxiv preprint

MX Cohen Morlet wavelet definition 5 of 14
selected and reported in a way that obscures the assumption underlying the data analysis. The key
goal of this paper is to present two different methods of formulating and describing Morlet wavelets
in a way that makes this assumption transparent and easily interpretable.
Typical definition of Morlet wavelets
A complex Morlet wavelet w can be defined as the product of a complex sine wave and a Gaussian
window:
(1)
where i is the imaginary operator ( ), f is frequency in Hz, and t is time in seconds. To avoid
introducing a phase shift, t should be centered at t=0 , for example, by defining t from -2 to +2
seconds. is the width of the Gaussian, which is defined as
(2)
The parameter that defines the time-frequency precision trade-off is n , which is often referred to as
the “number of cycles.” For neurophysiology data such as EEG, MEG, and LFP, typical values of n
range from 2 to 15 over frequencies between 2 Hz and 80 Hz. Other applications may require a
different number of cycles.
There is nothing “wrong” with equations 1 and 2. However, the relationship between the number of
cycles and the temporal-spectral smoothing is unclear, partly because most people do not think
about time in terms of “number of cycles,” and partly because the effect of n on the temporal
smoothing depends on the frequency of the wavelet (see Figure 2). Many researchers and students
struggle with how to specify and interpret this parameter, which leads to confusion and possibly
suboptimal data analyses.
A better definition of the Morlet wavelet
A definition of the complex Morlet wavelet that provides more clarity is
(3)
The new parameter here is h , which is the FWHM in seconds.
Equation 3 is not fundamentally different from equations 1-2. It is simply a way of rewriting the
formula to make the temporal smoothing parameter easier to define, understand, and report. Rather
than specifying a number of cycles (which might feel arbitrary and mysterious), one can specify a
FWHM in seconds (assuming that t is defined in seconds), which is a more natural unit to think about
in terms of desired temporal smoothing, and in terms of the assumption of the duration of
stationarity in the system under investigation.
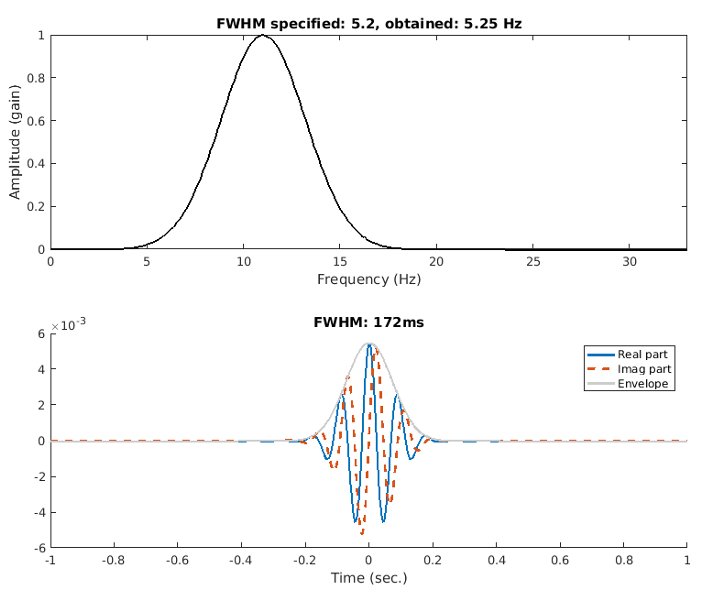
The h parameter in equation 3 is analytical; its actual implemented value depends on the data
sampling rate. For this reason, it is recommended to compute and examine the empirical FWHM that
is implemented in software. When the sampling rate is considerably higher than the frequency of
interest, the specified and empirical widths should match closely.
.CC-BY-NC-ND 4.0 International licenseavailable under a
not certified by peer review) is the author/funder, who has granted bioRxiv a license to display the preprint in perpetuity. It is made
The copyright holder for this preprint (which wasthis version posted August 21, 2018. ; https://doi.org/10.1101/397182doi: bioRxiv preprint