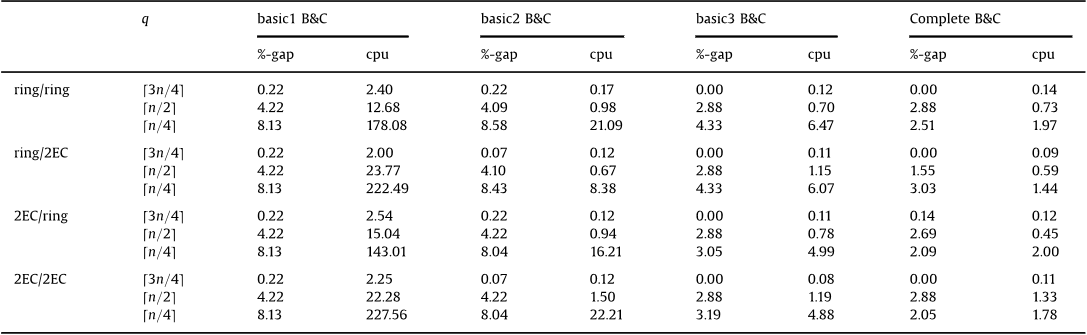
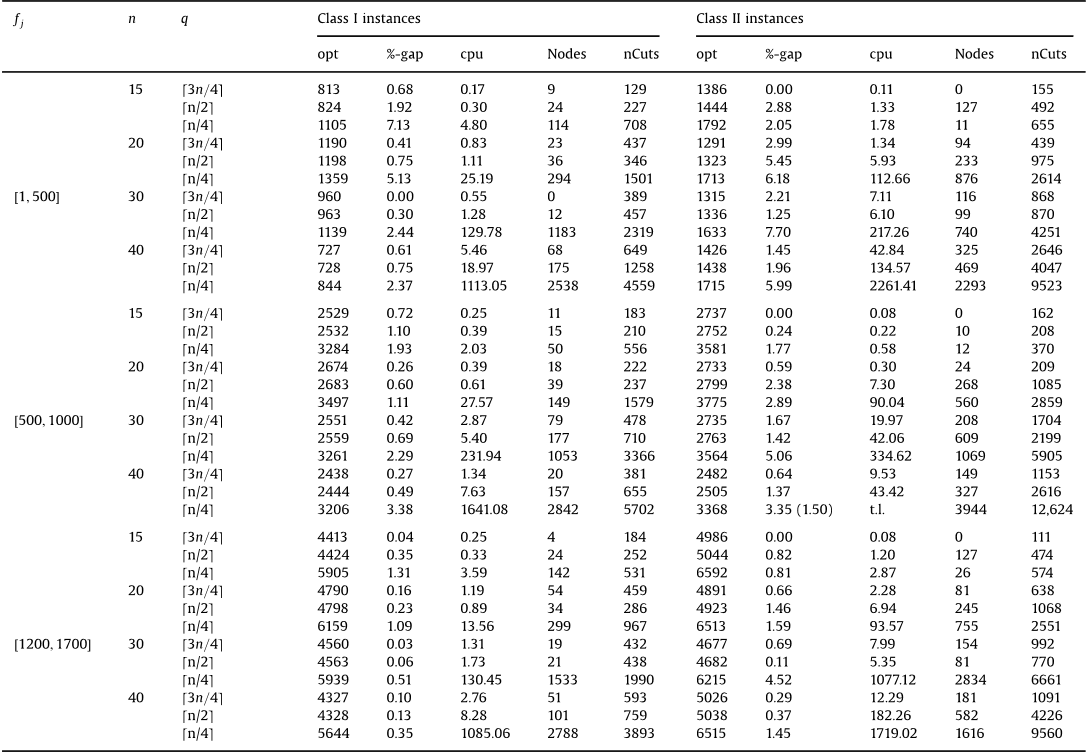
Abstract: Topology design of a distributed local area network (DLAN) is a complex optimization problem and has been generally modelled as a single-objective optimization problem. Traditionally, iterative techniques such as genetic algorithms and simulated annealing have been used to solve the problem. In this paper, we formulated the DLAN topology design problem as a multi-objective optimization problem considering five design objectives. These objectives are network reliability, network availability, average link utilization, monetary cost, and average network delay. The multi-objective nature of the problem has been addressed by incorporating a fuzzy goal programming approach to combine the individual design objectives into a single-objective function. The objective function is then optimized using the ant colony algorithm adapted for the problem. The performance of the proposed fuzzy goal programming-based ant colony optimization algorithm (GPACO) is evaluated with respect to the algorithm control parameters, namely pheromone deposit and evaporation rate, colony size and heuristic values. A comparative study was also done using four other multi-objective optimization algorithms which are non-dominated sorting genetic algorithm II, archived multi-objective simulated annealing algorithm, lexicographic ant colony optimization, and Pareto-dominance ant colony optimization. Results revealed that, in general, GPACO was able to find solutions of higher quality as compared to the other four algorithms.