
Lawrence Berkeley National Laboratory
Recent Work
Title
A broad exploration of nonlinear dynamics in microbial systems motivated by chemostat
experiments producing deterministic chaos.
Permalink
https://escholarship.org/uc/item/9wr5396s
Authors
Molz, Fred
Faybishenko, Boris
Agarwal, Deborah
Publication Date
2022-08-05
Peer reviewed
eScholarship.org Powered by the California Digital Library
University of California

1"
"
A"Broad"Exploration"of"Coupled"Nonlinear"Dynamics"in"Microbial"
Systems"Motivated"by"Chemostat"Experiments"Producing"
Deterministic"Chaos."
""
Fred"Molz
1
,"Boris"Faybishenko
2
"and"Deborah"Agarwal
3"
1
Environmental"Engineering"&"Earth"Sciences"Dept.,"Clemson"University,"342"Computer"Court,"
Anderson,"SC""29625.""
2
Energy"Geosciences"Division,"Earth"and"Environmental"Sciences"Area,"Lawrence"Berkeley"
National"Laboratory,"Berkeley,"CA""94720""
3
Computer"Research"Division,"Lawrence"Berkeley"National"Laboratory,"Berkeley,"CA""94720""
"
"
LBNL Report Number LBNL-2001172
"
"
"
"
"
"
"
"
Acknowledgements"BF"and"DA"research"supported"by"the"U.S."DOE,"Office"of"
Science,"Office"of"Biological"and"Environmental"Research,"and"Office"of"Science,"
Office"of"Advanced"Scientific"Computing"under"the"DOE"Contract"No."DE-AC02-
05CH11231."FM"acknowledges"the"support"of"the"Clemson"University,"
Department"of"Environmental"Engineering"and"Earth"Sciences."
"

2"
"
"
"
Table"of"Contents."
ABSTRACT."................................................................................................................"3"
Chapter"1:"Mathematical"Analysis"of"the"Becks"et"al."(1995)"Experiments."............."4"
1.1."Introduction."..................................................................................................."4"
1.2."Mathematical"Model"Development.".............................................................."7"
1.3."Results."......................................................................................................"13"
1.4."Discussion"and"Conclusions."........................................................................."21"
1.5."References."..................................................................................................."25"
S1.""Supplemental"Information"Concerning"Predator"Preference"Change."........."27"
Chapter"2:"Further"Study"of"the"Becks"et"al."Equations."........................................."30"
2.1."Introduction."................................................................................................."30"
2.2."Another"Model"Generalization."...................................................................."31"
2.3."Results."........................................................................................................."33"
2.4."Conclusions.".................................................................................................."38"
2.5."References."..................................................................................................."38"
Chapter"3.""Dimensionless"Forms"for"Equations"(1.10)."........................................."40"
3.1."Introduction."................................................................................................."40"
3.2."Dimensionless"Formulation."........................................................................."40"
3.3."Example"Solution"to"the"Dimensionless"Equations."....................................."44"
3.4."Results"and"Discussion."................................................................................"44"
3.5."References."..................................................................................................."51"
Chapter"4:""How"Might"Information"Theory"Relate"to"Chaotic"Dynamics"in"
Biological"Systems?"................................................................................................"52"
4.1."Introduction."................................................................................................."52"
4.2."Interpretation"of"Shannon’s"Measure."........................................................."53"
4.3."The"concept"of"Redundancy."........................................................................"58"
4.4."What"About"Continuous"Probability"Densities?"..........................................."62"
4.5."Calculation"of"Chaotic"Information"Measures."............................................."64"
4.6."Summary"and"Future"Research"Suggestions."..............................................."70"
4.7."References."..................................................................................................."74"
"
"

3"
"
!"#$%!&$'(
The$main$objective$of$this$report$is$to$develop$an$exploratory$mathematical$
analysis$motivated$by$the$Becks$et$al.$(2005)$experiments,$which$will$be$
presented$in$Chapter$1.$$Related$details$of$the$resulting$model$will$be$
presented$in$Chapter$2,$and$a$detailed$non-dimensionalization$will$follow$in$
Chapter$3.$$During$the$research$to$be$described,$a$potential$relationship$to$
Shannon$information$theory$was$realized,$and$this$will$be$developed$in$
Chapter$4.$$Several$avenues$for$future$research$are$suggested,$and$a$more$
mathematically-oriented$presentation$of$the$non-linear$dynamical$properties$
of$the$equations$developed$in$Chapter$1$may$be$found$in$Faybishenko$et$al.$
(2018).$$
"
"" "

4"
"
&)*+,-.(/0(1*,)-2*,34*5(!6*57838(9:(,)-("-4;8(-,(*5'(</==>?(@A+-.32-6,8'"
/'/'(B6 ,.9 C D4 ,396 ' (
$ Deterministic$chaotic$dynamics$in$biological$systems$has$not$received$as$
much$attention$as$that$in$electronic$or$fluid-mechanical$systems,$and$
mathematical$models$are$at$an$early$stage$of$development$(Faybishenko$and$
Molz$(2013).$$However,$this$has$started$to$change.$$Molz$and$Faybishenko$
(2013)$have$recently$concluded $that$three $pape rs$(Bec ks$et$al,$2005 ;$Graham $
et$al.$2007;$Beninca$et$al.,$2008),$using$experimental$studies$and$relevant$
mathematics,$may$provide$convincing$demonstrations$that$deterministic$
chaos$is$present$in$relatively$simple$biochemical$systems$of$an$ecological$
nature.$(See$Constantino$et$al.,$1997$for$additional$support.)$$For$example,$
Graham$et$al.$(2007)$reported$experimental$results$demonstrating$the$
phenomenon$of$chaotic$instability$in$biological$nitrification$in$a$controlled$
laboratory$environment.$$In$this$study,$the$aerob ic$biorea ctors$(ae rated $
containers$of$nutrient$solution$and$microbes)$were$filled$initially$with$a$
mixture$of$wastewater$from$a$treatment$plant$and$simulated$wastewater$
involving$a$mixt ur e$o f$m a n y$m ic rob e s.$T h e$m a in $v ar ia bl es $re cor d ed $a s$a $time$
series$were$total$bacteria,$ammonia-oxidizing$bacteria$(AOB),$nitrite-oxidizing$
bacteria$(NOB),$and$protozoa,$along$with$effluent$concentrations$of$nitrate,$
nitrite$and$total$ammonia.$$The$method$of$Rosenstein$et$al.$(1993)$was$used$to$
calculate$Lyapunov$exponents,$which$fell$roughly$in$a$range$from$0.05$to$$
0.2$d
-1
.$$Graham$et$al .$(2 0 0 7) $co n cl u d ed $th a t $“n itr ifica tio n $is $p ro n e$t o$c h a ot ic$
behavior$because$of$a$fragile$AOB-NOB$mutualism,”$i.e.,$interaction.$
$ Beninca$et$al.$(2008)$conducted$a$laboratory$experiment$over$a$period$$
$
$
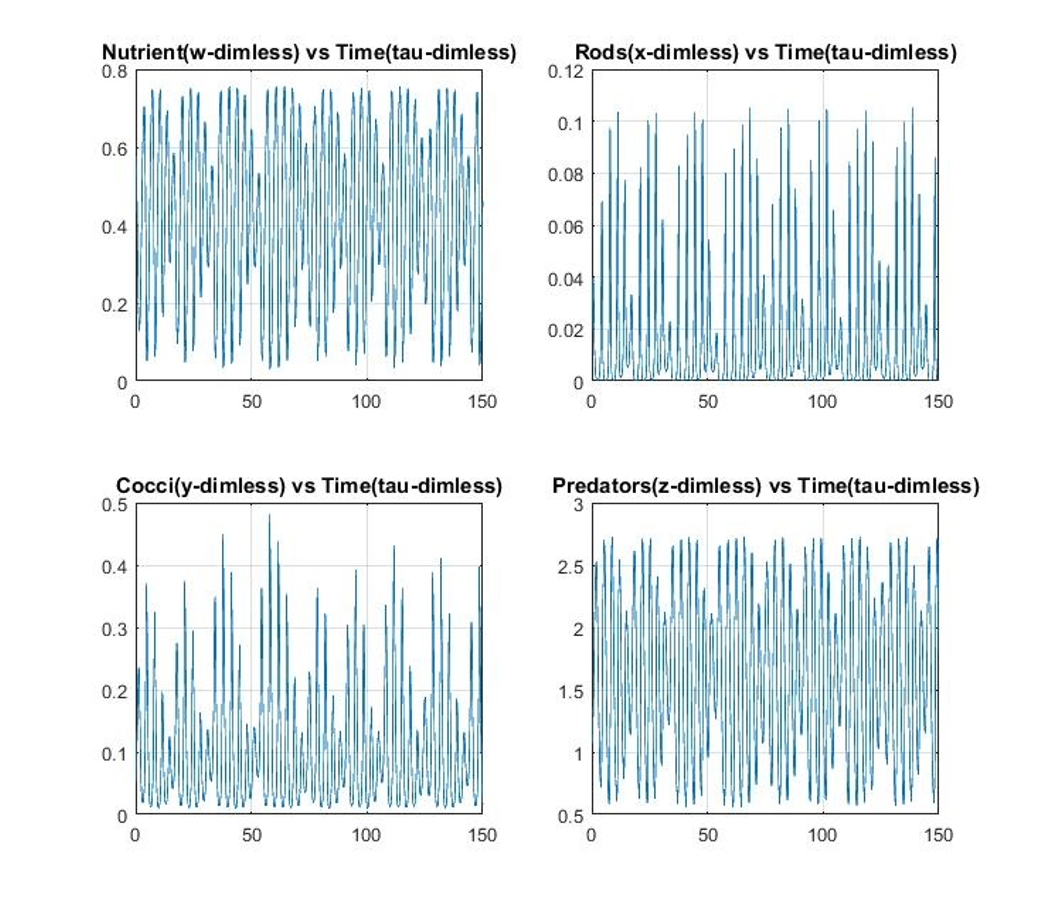

![Figure 2.3. 3-D system space plots of Equations (4) solution with an inflowing nutrient concentration given by Dn0 = [0.15(1 - 0.5sin(0.52t))]. A strange attractor is evident.](/figures/figure-2-3-3-d-system-space-plots-of-equations-4-solution-2i9a6qsj.png)

![Figure 1.6. Simulated nutrient and microbe dynamics that match the Becks et al. [2005, Fig. 1] results for D = 0.9/d (0.0375/hr).](/figures/figure-1-6-simulated-nutrient-and-microbe-dynamics-that-3u6k06k2.png)
