Q1. What are the contributions mentioned in the paper "A cartesian grid embedded boundary method for the heat equation on irregular domains" ?
The authors present an algorithm for solving the heat equation on irregular time-dependent domains.
A Cartesian grid embedded boundary method for the heat equation on irregular domains
13 Nov 2001-Journal of Computational Physics (Academic Press Professional, Inc.)-Vol. 173, Iss: 2, pp 620-635
TL;DR: An algorithm for solving the heat equation on irregular time-dependent domains is presented, based on the Cartesian grid embedded boundary algorithm of Johansen and Colella, combined with a second-order accurate discretization of the time derivative.
About: This article is published in Journal of Computational Physics.The article was published on 2001-11-13 and is currently open access. It has received 161 citations till now. The article focuses on the topics: Mixed boundary condition & Boundary (topology).
Summary (1 min read)
1. INTRODUCTION
- For the time discretization, for the fixed-boundary problem the authors use either the Crank-Nicolson method or the method of Twizell, Gumel and Arigu (TGA) [10] .
- The authors algorithm is stable and achieves second-order accuracy both on problems with fixed domain and on problems with a time-dependent domain (t) with boundaries moving with constant velocities.
FIG. 1.
- Centers of cells in (t old ) are shown with solid circles, and centers of cells in (tnew) -(t old ) are shown with unfilled circles.
- The authors solve (19) numerically on a rectangular domain with three elliptically-shaped holes, with boundary conditions computed using the exact solution (18).
- In the moving-boundary problem, the holes move with constant velocities.
- With both fixed and moving boundaries, the authors solve two separate problems with different boundary conditions: Dirichlet conditions on all boundaries; Dirichlet conditions on the fixed external boundaries, but Neumann conditions on the boundaries of the ellipses.
Did you find this useful? Give us your feedback
Figures (15)
TABLE 3 
FIG. 6. Contour plots of absolute value of solution error to (19) at t = 1 for fixed boundaries, Dirichlet boundary conditions, h = 0:0125. Top figure is for Crank–Nicolson method, bottom figure for TGA method. 
FIG. 4. Solution error at t = 1 using Crank–Nicolson (stars) and TGA (circles), for the Dirichlet problem for (19) with fixed boundaries. Left-hand plot shows max norm, right-hand plot shows 1-norm. We see that both jj jj1 = O(h2) and jj jj1 = O(h2), indicating second-order accuracy. 
FIG. 5. Solution error at t = 1 using Crank–Nicolson (stars) and TGA (circles), for the Neumann problem for (19) with fixed boundaries. Left-hand plot shows max norm, right-hand plot shows 1-norm. We see that both jj jj1 = O(h2) and jj jj1 = O(h2), indicating second-order accuracy. 
FIG. 8. Contour plot of exact solution to (19) at t = 1 for moving-boundaryproblem. The dashed ellipses indicate the boundaries at t = 0. 
TABLE 1 
TABLE 2 Parameters for ellipses in (20), where = p 2=15 = 0:09428. 
FIG. 3. Contour plot of exact solution (18) to (19) at t = 1 with fixed boundaries. 
FIG. 10. Solution error at t = 1 in TGA method (circles) and Crank–Nicolson (stars), with Neumann conditions for (19) on moving boundaries. Left-hand plot shows max norm, right-hand plot shows 1-norm. 
FIG. 9. Solution error at t = 1 in TGA method (circles) and Crank–Nicolson method (stars), with Dirichlet conditions for (19) on moving boundaries. Left-hand plot shows max norm, right-hand plot shows 1-norm. 
FIG. 1. Centers of cells in (told) are shown with solid circles, and centers of cells in (tnew) - (told) are shown with unfilled circles. To estimate the value of U n at one of these latter points, we interpolate quadratically from values at the centers of three other cells in (told) forming a line with the new cell center. We pick whichever such line is closest in direction to the normal to the boundary at time t new. 
FIG. 2. From known values at points shown with solid circles on the moving boundary, we extrapolate to find values of (Dirichlet) or @ @n (Neumann) at points shown with unfilled circles, representing times told and tint on the boundary at time tnew. 
FIG. 11. Contour plot of absolute value of solution error to (19) at t = 1 for moving boundaries, Dirichlet boundary conditions, h = 0:0125 in TGA method. 
FIG. 12. Contour plot of absolute value of solution error to (19) at t = 1 for moving boundaries, Neumann boundary conditions, h = 0:0125 in TGA method. 
FIG. 7. Contour plots of absolute value of solution error to (19) at t = 1 for fixed boundaries, Neumann boundary conditions, h = 0:0125. Top figure is for Crank–Nicolson method, bottom figure for TGA method.
Citations
More filters
15 Apr 2009
TL;DR: A new immersed interface method, the algebraic immersed interface and boundary (AIIB) method, is presented for elliptic equations with immersed interface problems to create auxiliary unknowns at existing grid locations in order to increase the degrees of freedom of the initial problem.
Abstract: A new immersed interface method, the algebraic immersed interface and boundary (AIIB) method, is presented for elliptic equations with immersed interface problems. This method allows accurate discontinuous conditions on immersed boundaries and interfaces to be imposed. The main idea is to create auxiliary unknowns at existing grid locations in order to increase the degrees of freedom of the initial problem. These auxiliary nodes allow to impose various constraints to the system on interfaces of complex shapes. For instance, the method is able to deal with immersed interfaces for elliptic equations with jump conditions on the solution or discontinuous coefficients at a second order of spatial accuracy. As the AIIB method acts on an algebraic level and only changes the problem matrix, no particular attention to the initial discretization is required. The method can be easily implemented in any structured or unstructured grid code. Several validation problems are presented to demonstrate the interest and accuracy of the method.
5 citations
Cites methods from "A Cartesian grid embedded boundary ..."
...Cartesian grid methods [13, 20] propose using a structured grid in the whole domain except near obstacles where unstructured cells are created from structured cells....
[...]
01 Jun 2012
TL;DR: In this paper, the authors present a front tracking method for the solution of the governing equations of motion for two-phase micromixing of incompressible, viscous, liquid-liquid solvent extraction processes.
Abstract: This progress report describes the development of a front tracking method for the solution of the governing equations of motion for two-phase micromixing of incompressible, viscous, liquid-liquid solvent extraction processes. The ability to compute the detailed local interfacial structure of the mixture allows characterization of the statistical properties of the two-phase mixture in terms of droplets, filaments, and other structures which emerge as a dispersed phase embedded into a continuous phase. Such a statistical picture provides the information needed for building a consistent coarsened model applicable to the entire mixing device. Coarsening is an undertaking for a future mathematical development and is outside the scope of the present work. We present here a method for accurate simulation of the micromixing dynamics of an aqueous and an organic phase exposed to intense centrifugal force and shearing stress. The onset of mixing is the result of the combination of the classical RayleighTaylor and Kelvin-Helmholtz instabilities. A mixing environment that emulates a sector of the annular mixing zone of a centrifugal contactor is used for the mathematical domain. The domain is small enough to allow for resolution of the individual interfacial structures and large enough to allow for an analysis of their statistical distribution of sizes and shapes. A set of accurate algorithms for this application requires an advanced front tracking approach constrained by the incompressibility condition. This research is aimed at designing and implementing these algorithms. We demonstrate verification and convergence results for one-phase and unmixed, two-phase flows. In addition we report on preliminary results for mixed, two-phase flow for realistic operating flow parameters.
5 citations
Cites methods from "A Cartesian grid embedded boundary ..."
...It was generalized to parabolic equations with a moving boundary (McCorquodale et al., 2001), three-dimensional elliptic and parabolic equations (Schwartz et al....
[...]
TL;DR: A comprehensive theoretical analysis of the numerical issues, which arise when dealing with domains, whose boundaries evolve smoothly in the spatial domain as a function of time, and which can achieve higher than 2nd-order accuracy both in time and space.
Abstract: This paper considers a family of spatially discrete approximations, including boundary treatment, to initial boundary value problems in evolving bounded domains. The presented method is based on the Cartesian grid embedded Finite-Difference method, which was initially introduced by Abarbanel and Ditkowski (ICASE Report No. 96-8, 1996; and J. Comput. Phys. 133(2), 1997) and Ditkowski (Ph.D. thesis, Tel Aviv University, 1997), for initial boundary value problems on constant irregular domains.
We perform a comprehensive theoretical analysis of the numerical issues, which arise when dealing with domains, whose boundaries evolve smoothly in the spatial domain as a function of time. In this class of problems the moving boundaries are impenetrable with either Dirichlet or Neumann boundary conditions, and should not be confused with the class of moving interface problems such as multiple phase flow, solidification, and the Stefan problem.
Unlike other similar works on this class of problems, the resulting method is not restricted to domains of up to 3-D, can achieve higher than 2nd-order accuracy both in time and space, and is strictly stable in semi-discrete settings. The strict stability property of the method also implies, that the numerical solution remains consistent and valid for a long integration time.
A complete convergence analysis is carried in semi-discrete settings, including a detailed analysis for the implementation of the diffusion equation. Numerical solutions of the diffusion equation, using the method for a 2nd and a 4th-order of accuracy are carried out in one dimension and two dimensions respectively, which demonstrates the efficacy of the method.
5 citations
12 May 2005
TL;DR: In this paper, the authors present simulation results from a new computational model of DNA flow in microfluidic devices, based on a fully coupled fluid-particle numerical algorithm with both stochastic and deterministic components in a bead-rod polymer representation.
Abstract: We present simulation results from a new computational model of DNA flow in microfluidic devices. This work is important because computational models are needed to design miniaturized biomedical devices that are becoming the state-of-the-art in many significant applications including pathogen detection as well as continuous monitoring and drug delivery. Currently advanced algorithms in design tools are non-existent but necessary to understand the complex fluid and polymer dynamics involved in biological flow at small scales. Our model is based on a fully coupled fluid-particle numerical algorithm with both stochastic and deterministic components in a bead-rod polymer representation. We have applied this work to DNA extraction configurations in a microfluidic PCR chamber used in a pathogen detection system. We demonstrate our method on the test problem of flow of a single DNA molecule in a 2D packed array microchannel. We are also investigating mechanisms for molecular "sticking" using short range forces.
5 citations
Cites methods from "A Cartesian grid embedded boundary ..."
...Irregular geometry boundaries are treated with an embedded boundary, or cutcell, Cartesian grid method [3], [4]....
[...]
TL;DR: In this paper, the authors proposed an innovative numerical method for simulating the interaction of fluid with irregularly shaped stationary structures based on Cartesian grids, where the boundary velocities close to the immersed solid boundary can be determined in terms of the level set function and the neighboring fluid velocity.
Abstract: Summary
This work proposes an innovative numerical method for simulating the interaction of fluid with irregularly shaped stationary structures based on Cartesian grids. Instead of prescribing an artificial force to enforce the no-slip boundary condition at the solid–fluid interface, this work imposes two boundary velocities, referred to as the solid and mass-conserving boundary velocities, to satisfy the no-slip boundary condition and mass conservation in the ghost cells around the immersed solid boundary. Both the traditional level set method [41] and the hybrid particle level set method [45] were used to represent the solid boundary and the complex free-surface evolution, respectively. Consequently, the boundary velocities close to the immersed solid boundary can be determined in terms of the level set function and the neighboring fluid velocity. The projection method is further modified to incorporate the solid and mass-conserving boundary velocities into the solution algorithm. A series of numerical experiments were conducted to demonstrate the feasibility of the proposed method. They involved uniform flow past a stationary circular cylinder and the propagation of water waves over a submerged trapezoidal breakwater. Comparisons between the numerical results and experimental data showed very good agreement in all cases of interest. Copyright © 2015 John Wiley & Sons, Ltd.
5 citations
References
More filters
[...]
40,330 citations
Additional excerpts
...Similar approaches based on formally inconsistent discretizations at the irregular boundary have been used previously and observed to be stable [1, 9], so we expect that the extension to the more accurate boundary discretization should be straightforward....
[...]
Book•
07 Jan 2013
TL;DR: In this article, Leray-Schauder and Harnack this article considered the Dirichlet Problem for Poisson's Equation and showed that it is a special case of Divergence Form Operators.
Abstract: Chapter 1. Introduction Part I: Linear Equations Chapter 2. Laplace's Equation 2.1 The Mean Value Inequalities 2.2 Maximum and Minimum Principle 2.3 The Harnack Inequality 2.4 Green's Representation 2.5 The Poisson Integral 2.6 Convergence Theorems 2.7 Interior Estimates of Derivatives 2.8 The Dirichlet Problem the Method of Subharmonic Functions 2.9 Capacity Problems Chapter 3. The Classical Maximum Principle 3.1 The Weak Maximum Principle 3.2 The Strong Maximum Principle 3.3 Apriori Bounds 3.4 Gradient Estimates for Poisson's Equation 3.5 A Harnack Inequality 3.6 Operators in Divergence Form Notes Problems Chapter 4. Poisson's Equation and Newtonian Potential 4.1 Holder Continuity 4.2 The Dirichlet Problem for Poisson's Equation 4.3 Holder Estimates for the Second Derivatives 4.4 Estimates at the Boundary 4.5 Holder Estimates for the First Derivatives Notes Problems Chapter 5. Banach and Hilbert Spaces 5.1 The Contraction Mapping 5.2 The Method of Cintinuity 5.3 The Fredholm Alternative 5.4 Dual Spaces and Adjoints 5.5 Hilbert Spaces 5.6 The Projection Theorem 5.7 The Riesz Representation Theorem 5.8 The Lax-Milgram Theorem 5.9 The Fredholm Alternative in Hilbert Spaces 5.10 Weak Compactness Notes Problems Chapter 6. Classical Solutions the Schauder Approach 6.1 The Schauder Interior Estimates 6.2 Boundary and Global Estimates 6.3 The Dirichlet Problem 6.4 Interior and Boundary Regularity 6.5 An Alternative Approach 6.6 Non-Uniformly Elliptic Equations 6.7 Other Boundary Conditions the Obliue Derivative Problem 6.8 Appendix 1: Interpolation Inequalities 6.9 Appendix 2: Extension Lemmas Notes Problems Chapter 7. Sobolev Spaces 7.1 L^p spaces 7.2 Regularization and Approximation by Smooth Functions 7.3 Weak Derivatives 7.4 The Chain Rule 7.5 The W^(k,p) Spaces 7.6 DensityTheorems 7.7 Imbedding Theorems 7.8 Potential Estimates and Imbedding Theorems 7.9 The Morrey and John-Nirenberg Estimes 7.10 Compactness Results 7.11 Difference Quotients 7.12 Extension and Interpolation Notes Problems Chapter 8 Generalized Solutions and Regularity 8.1 The Weak Maximum Principle 8.2 Solvability of the Dirichlet Problem 8.3 Diferentiability of Weak Solutions 8.4 Global Regularity 8.5 Global Boundedness of Weak Solutions 8.6 Local Properties of Weak Solutions 8.7 The Strong Maximum Principle 8.8 The Harnack Inequality 8.9 Holder Continuity 8.10 Local Estimates at the Boundary 8.11 Holder Estimates for the First Derivatives 8.12 The Eigenvalue Problem Notes Problems Chapter 9. Strong Solutions 9.1 Maximum Princiles for Strong Solutions 9.2 L^p Estimates: Preliminary Analysis 9.3 The Marcinkiewicz Interpolation Theorem 9.4 The Calderon-Zygmund Inequality 9.5 L^p Estimates 9.6 The Dirichlet Problem 9.7 A Local Maximum Principle 9.8 Holder and Harnack Estimates 9.9 Local Estimates at the Boundary Notes Problems Part II: Quasilinear Equations Chapter 10. Maximum and Comparison Principles 10.1 The Comparison Principle 10.2 Maximum Principles 10.3 A Counterexample 10.4 Comparison Principles for Divergence Form Operators 10.5 Maximum Principles for Divergence Form Operators Notes Problems Chapter 11. Topological Fixed Point Theorems and Their Application 11.1 The Schauder Fixes Point Theorem 11.2 The Leray-Schauder Theorem: a Special Case 11.3 An Application 11.4 The Leray-Schauder Fixed Point Theorem 11.5 Variational Problems Notes Chapter 12. Equations in Two Variables 12.1 Quasiconformal Mappings 12.2 holder Gradient Estimates for Linear Equations 12.3 The Dirichlet Problem for Uniformly Elliptic Equations 12.4 Non-Uniformly Elliptic Equations Notes Problems Chapter 13. Holder Estimates for
18,443 citations
01 Jan 1997
TL;DR: In this paper, a class of partial differential equations that generalize and are represented by Laplace's equation was studied. And the authors used the notation D i u, D ij u for partial derivatives with respect to x i and x i, x j and the summation convention on repeated indices.
Abstract: We study in this chapter a class of partial differential equations that generalize and are to a large extent represented by Laplace’s equation. These are the elliptic partial differential equations of second order. A linear partial differential operator L defined by
$$ Lu{\text{: = }}{a_{ij}}\left( x \right){D_{ij}}u + {b_i}\left( x \right){D_i}u + c\left( x \right)u $$
is elliptic on Ω ⊂ ℝ n if the symmetric matrix [a ij ] is positive definite for each x ∈ Ω. We have used the notation D i u, D ij u for partial derivatives with respect to x i and x i , x j and the summation convention on repeated indices is used. A nonlinear operator Q,
$$ Q\left( u \right): = {a_{ij}}\left( {x,u,Du} \right){D_{ij}}u + b\left( {x,u,Du} \right) $$
[D u = (D 1 u, ..., D n u)], is elliptic on a subset of ℝ n × ℝ × ℝ n ] if [a ij (x, u, p)] is positive definite for all (x, u, p) in this set. Operators of this form are called quasilinear. In all of our examples the domain of the coefficients of the operator Q will be Ω × ℝ × ℝ n for Ω a domain in ℝ n . The function u will be in C 2(Ω) unless explicitly stated otherwise.
8,299 citations
"A Cartesian grid embedded boundary ..." refers background in this paper
...However, it is well known that, for any domain with smooth boundary, a smooth function can be extended to all of R with a bound on the relative increase in the C norms that depends only on the domain and (k; ) [5]....
[...]
TL;DR: In this paper, a second-order projection method for the Navier-Stokes equations is proposed, which uses a specialized higher-order Godunov method for differencing the nonlinear convective terms.
1,287 citations
"A Cartesian grid embedded boundary ..." refers methods in this paper
...The method described here, together with that in [6] for elliptic PDEs and [8] for hyperbolic PDEs, provide the fundamental components required for developing second-order accurate methods for a broad range of continuum mechanics problems in irregular geometries based on the predictor–corrector approach in [2]....
[...]
TL;DR: A numerical method for solving Poisson's equation, with variable coefficients and Dirichlet boundary conditions, on two-dimensional regions using a finite-volume discretization, which embeds the domain in a regular Cartesian grid.
470 citations
"A Cartesian grid embedded boundary ..." refers background or methods in this paper
...As in previous work on elliptic problems [6], our approach uses a finite-volume discretization, which embeds the domain in a regular Cartesian grid....
[...]
...We follow the approach described in [6, 7]....
[...]
...With Dirichlet boundary conditions as from (3), we compute an estimate of ∂ψ ∂n by interpolating from the grid values and the values at the boundaries; for details, see [6]....
[...]
...The method described here, together with that in [6] for elliptic PDEs and [8] for hyperbolic PDEs, provide the fundamental components required for developing second-order accurate methods for a broad range of continuum mechanics problems in irregular geometries based on the predictor–corrector approach in [2]....
[...]
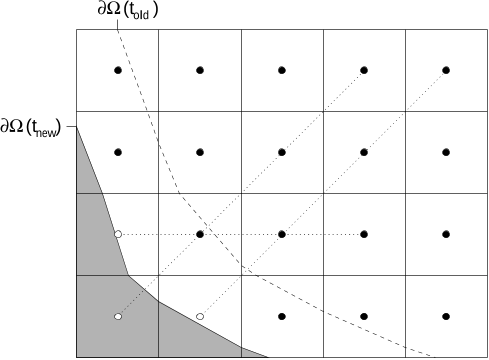
...This is routine for the case in which the embedded boundary is contained in the finest level of refinement [6], but requires some additional discretization design when the embedded boundary crosses coarse–fine interfaces....
[...]