



Did you find this useful? Give us your feedback







17 citations
...It is also widely investigated how certain restrictions on P systems with active membrane affect the computation power of these systems (see for example [6, 8, 9, 11, 13, 14, 16, 17, 19, 20, 25])....
[...]
14 citations
...AC or L), then we conjecture that a P lowerbound can be found by improving a result in [6]....
[...]
...What is the lowerbound on the power of the systems that we consider? If P uniformity is used, then we get a trivial P lowerbound [6]....
[...]
...Given a (properly encoded) set of rules for a membrane system Π, the dependency graph GΠ is created in logspace [6]....
[...]
10 citations
...In this paper and others [33, 34, 35, 36, 37], we have put forward the idea of exploring the power of membrane systems under tight uniformity conditions....
[...]
7 citations
6 citations
366 citations
...In this paper we explore the computational power of cell division (mitosis) and dissolution (apoptosis) by investigating a variant of the model called active membranes [13]....
[...]
...G. Păun....
[...]
...These definitions are from Păun [13, 14], and Sośık and Rodŕıguez-Patón [18]....
[...]
...These definitions are from Păun [13, 14], and Sośık and Rodŕıguez-Patón [18]....
[...]
333 citations
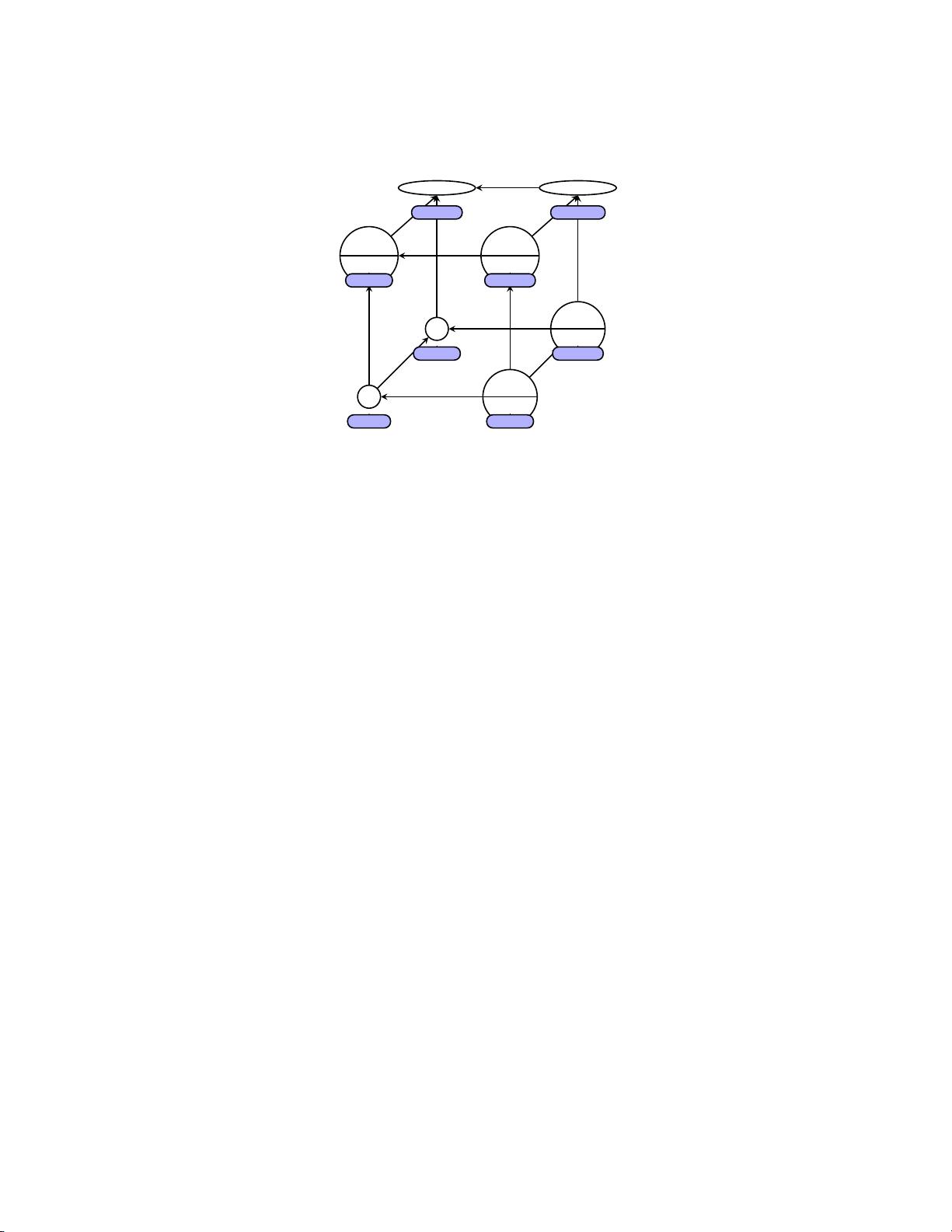
...A constant time CRAM encodes an instance of the Circuit Value problem (CVP) [10] as a PMCAM0+d,+u membrane system using the gadget membranes and rules shown in Figure 2....
[...]
...The resulting membrane system directly solves the instance of CVP in polynomial time....
[...]
194 citations
...Previous work on the computational complexity of membrane systems used (Turing machine) polynomial time uniformity [16]....
[...]
139 citations
...In this paper we are using DLOGTIME-AC0-uniformity which can be somewhat cumbersome to analyse, therefore in our proofs we use an AC0 equivalent model called the constant time Concurrent Random Access Machine (constant time CRAM) [2, 8]....
[...]
...A constant time CRAM encodes an instance of the Circuit Value problem (CVP) [10] as a PMCAM0+d,+u membrane system using the gadget membranes and rules shown in Figure 2....
[...]
...A CRAM to construct the above family for this restricted version of STCON will run in d+ 1 time steps....
[...]
...Each processor of the CRAM works with one edge of the graph....
[...]
...In this paper we are using DLOGTIME-AC-uniformity which can be somewhat cumbersome to analyse, therefore in our proofs we use an AC equivalent model called the constant time Concurrent Random Access Machine (constant time CRAM) [2, 8]....
[...]