A comparison of different nonparametric methods for inference on
additive models
Holger Dette
Ruhr-Universit¨at Bochum
Fakult¨at f¨ur Mathematik
D - 44780 Bochum, Germany
Carsten von Lieres und Wilkau
Ruhr-Universit¨at Bochum
Fakult¨at f¨ur Mathematik
D - 44780 Bochum, Germany
Stefan Sperlich
Universidad Carlos III de Madrid
Departamento de Estad´ıstica y Econometr´ıa
E - 28903 Getafe, Spain
May 10, 2001
Abstract
In this article we highlight the main differences of available methods for the analysis of regression
functions that are probably additive separable. We first discuss definition and interpretation of the
most common estimators in practice. This is done by explaining the different ideas of modeling
behind each estimator as well as what the procedures are doing to the data. Computational
aspects are mentioned explicitly. The illustrated discussion concludes with a simulation study on
the mean squared error for different marginal integration approaches. Next, various test statistics
for checking additive separability are introduced and accomplished with asymptotic theory. Based
on the asymptotic results under hypothesis as well as under the alternative of non additivity we
compare the tests in a brief discussion. For the various statistics, different smoothing and bootstrap
methods we perform a detailed simulation study. A main focus in the reported results is directed on
the (non-) reliability of the methods when the covariates are strongly correlated among themselves.
Again, a further point are the computational aspects. We found that the most striking differences
lie in the different pre-smoothers that are used, but less in the different constructions of test
statistics. Moreover, although some of the observed differences are strong, they surprisingly can
not be revealed by asymptotic theory.
1
AMS Subject Classification: 62G07, 62G10
Keywords: marginal integration, additive models, test of additivity.
1
Acknowledgements: This research was financially supported by the Spanish “Direcci´on General de Ense˜nanza Supe-
rior” (DGES), reference number PB98-0025 and the Deutsche Forschungsgemeinschaft (SFB 475: Komplexit¨atsreduktion
in multivariaten Datenstrukturen, Teilprojekt A2; Sachbeihilfe: Validierung von Hypothesen, De 502/9-1). Parts of
this paper were written while the first author was visiting Perdue University and this author would like to thank the
Department of Statistics for its hospitality.
1

1 Introduction
In the last ten years additive models have attracted an increasing amount of interest in nonparametric
statistics. Also in the econometric literature these methods have a long history and are widely used
today in both, theoretical considerations and empirical research. Deaton and M¨ullbauer (1980) pro-
vided many examples in microeconomics where the additive structure follows from economic theory
of separable decision making like two step budgeting or optimization. Furthermore, additivity is the
natural structure when production processes have independent substitution rates for separable goods.
In statistics, additivity leads to the circumvention of the curse of dimensionality (see Stone 1985) that
usually affects multidimensional nonparametric regression.
The most common and best known nonparametric estimation approaches in these models can be
divided into three main groups: the backfitting (see Buja, Hastie and Tibshirani 1989, or Hastie and
Tibshirani 1990 for algorithms, and Opsomer and Ruppert 1997 or Mammen, Linton and Nielsen 1999),
series estimators (see Andrews and Whang 1990 or Li 2000), and the marginal integration estimator
(see Tjøstheim and Auestad 1994, Linton and Nielsen 1995, and also Kim, Linton, Hengartner 2000
for an important modification). Certainly, here we have mentioned only the main references respective
basic ideas and theory. Among them, to our knowledge, the series estimator is so far not explored in
practice, i.e. although straightforward implementation and good performance is declared, we could not
find a simulation study or an application of this method. Moreover, usually hardly feasible assumptions
are made on the series and its “smoothing parameters”, e.g. reducing bias and variance simultaneously,
but without giving a correct idea how to choose them in practice. The backfitting of Buja, Hastie and
Tibshirani (1989) is maybe the most studied additive model estimator in practice, and algorithms are
developed for various regression problems. However, the backfitting version of Mammen, Linton and
Nielsen (1999), for which closed theory is provided but no Monte-Carlo studies, differs a lot in definition
and implementation from that one. The marginal integration, finally, has experienced most extensions
in theory but actually a quite different interpretation than the aforementioned estimators. This was
first theoretically highlighted by Nielsen and Linton (1997) and empirically investigated by Sperlich,
Linton and H¨ardle (1999) in a detailed simulation study. The main point is that backfitting, at least the
version of Mammen et al. (1999), and series estimators are orthogonal projections of the regression
into the additive space whereas the marginal integration estimator always estimates the marginal
impact of the explanatory variables taking into account possible correlation among them. This led
Pinske (2000) to the interpretation of the marginal integration estimator as a consistent estimator of
weak separable components, which, in the case of additivity, coincide with the additive components.
From this it can be expected that the distance between the real regression function and its estimate
increases especially fast when the data generating regression function is not additive but estimated by
the sum of component estimates obtained from marginal integration instead of backfitting or series
estimates. A consequence could be to prefer marginal integration for the construction of additivity
tests. Nevertheless, until now backfitting was not used for testing simply because of the lack of theory
for the estimator.
Due to the mentioned econometric results and statistical advantages there is an increasing interest in
testing the additive structure. Eubank, Hart, Simpson and Stefanski (1995) constructed such a test but
used special series estimates that apply only on data observed on a grid. Gozalo and Linton (2000) as
well as Sperlich, Tjøstheim and Yang (2000) introduced a bootstrap based additivity test applying the
marginal integration. Here, Sperlich et al. (2000) concentrated on the analysis of particular interaction
terms rather than on general separability. Finally, Dette and von Lieres (2000) have summarized the
2

test statistics considered by Gozalo and Linton (2000) and compared them theoretically and also in a
small simulation study. Their motivation for using the marginal integration was its direct definition
which allows an asymptotic treatment of the test statistics using central limit theorems for degenerate
U-statistics. They argued that such an approach based on backfitting seems to be intractable, because
their asymptotic analysis does not require the asymptotic properties of the estimators as e.g. derived
by Mammen, Linton and Nielson (1999) but an explicit representation of the residuals. Further, Dette
and Munk (1998) pointed out several drawbacks in the application of Fourier series estimation for
checking model assumptions. For these and the former mentioned reasons we do not consider series
estimators for the construction of tests for additivity in this paper.
For the empirical researcher it would be of essential interest how the different methods perform in
finite samples and which method should be preferred. Therefore the present article is mainly concerned
about the practical performance of the different procedures and for a better understanding of some of
the above mentioned problems in estimating and testing. Hereby, the main part studies performance,
feasibility and technical differences of estimation respectively testing procedures based on different
estimators. We concentrate especially on the differences caused by the use of different (pre-)smoothers
in marginal integration, in particular on the classic approach of Linton and Nielsen (1995) and on the
internalized Nadaraya–Watson estimator (Jones, Davies and Park 1994) as suggested by Kim, Linton
and Hengartner (2000). Notice that this study is not thought as an illustration of the general statement
of consistency and convergence. Our main interest is directed to the investigation and comparison of
finite sample behavior of these procedures.
The marginal integration estimator becomes inefficient with increasing correlation in the regressors,
see Linton (1997). He suggested to combine the marginal integration with a one step backfitting
afterwards to reach efficiency. Unfortunately, this combination destroys any interpretability of the
estimate when the additivity assumption is violated. The same loss of efficiency was also observed
in a simulation study by Sperlich, Linton and H¨ardle (1999) for the backfitting estimator, although
these results do not reflect the asymptotic theory. In their article it is further demonstrated that with
increasing dimension the additive components are still estimated with a reasonable precision, whereas
the estimation of the regression function becomes problematic. This fact could cause problems for
prediction and for bootstrap tests. We will investigate and explain that the use of the internalized
Nadaraya–Watson estimator for the marginal integration can partly ameliorate this problem. This is
actually not based on theoretical results but more on numerical circumstances respective the handling
of “poor data areas”. Throughout this paper we will call the classical marginal integration estimator
CMIE, and IMIE the one using the internalized Nadaraya–Watson estimator as multidimensional
pre-smoother.
The rest of the paper is organized as follows. In Section 2 we give the definitions of the analyzed
estimators and some more discussion about their advantages and disadvantages. Finally we provide
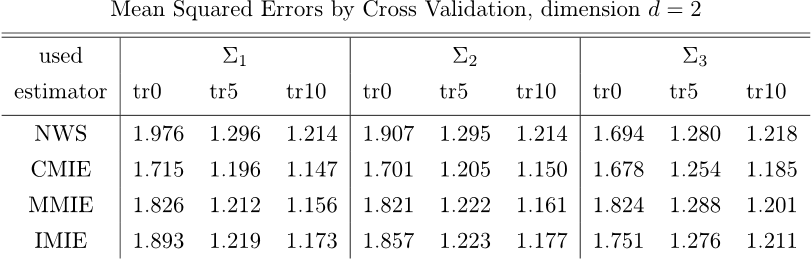
some simulation results on the Cross-Validation mean squared errors for the different methods of
estimation. In Section 3 we introduce various test statistics based in the IMIE to check the additivity
assumption, present closed form asymptotic theory and a theoretical comparison. Notice that for
the IMIE, at least for testing, little theory has been done until now and hardly empirical studies.
Therefore we provide both in this work, an extensive simulation study but also a closed theory about
the asymptotic properties for any new estimator and test we are considering. Section 4 finally is
dedicated to an intensive simulation study for these test statistics, all using bootstrap methods. The
proofs of the asymptotic results are cumbersome and deferred to the Appendix in Section 5.
3

2 Marginal Integration and Additive Models
Let us consider the general regression model
Y = m(X)+σ(X)ε (2.1)
where X =(X
1
,...,X
d
)
T
is a d-dimensional random variable with density f, Y is the real valued
response, and ε the error, independent of X with mean 0 and variance 1. Further, m, σ are unknown
(smooth) functions and the regression function m(·) has to be estimated nonparametrically. As in-
dicated above the marginal integration estimator is constructed to catch the marginal impact of one
or some regressors X
α
∈ IR
d
α
, d
α
<d. For the ease of notation we will restrict ourselves to the case
d
α
=1forallα. Notice first that in case of additivity, i.e. there exist functions m
α
, m
−α
such that
m(X)=m
α
(X
α
)+m
−α
(X
−α
) (2.2)
with X
−α
being the vector X without the component X
α
, the marginal impact of X
α
corresponds
exactly to the additive component m
α
. For identification we set E[m
α
(X
α
)] = 0 and consequently
E[Y ]=E[m
−α
(X
−α
)] = c. The marginal integration estimator is defined noting that
E
X
−α
[m(x
α
,X
−α
)] =
m(x
α
,x
−α
)f
−α
(x
−α
)dx
−α
(2.3)
= E
X
−α
[m
−α
(X
−α
)+m
α
(x
α
)] = c + m
α
(x
α
), (2.4)
where f
−α
denotes the marginal density of X
−α
, and the second line follows from the first line in the
case of additivity, see equation (2.2). So marginal integration yields the function m
α
up to a constant
that can easily be estimated by the average over the observations Y
i
. We estimate the right hand
side of equation (2.3) by replacing the expectation by an average and the unknown mutidimensional
regression function m by a pre-smoother ˜m. Certainly, having a completely additive separable model
of the form
m(X)=c +
d
α=1
m
α
(X
α
), (2.5)
this method can be applied to estimate all components m
α
, and finally the regression function m is
estimated by summing up an estimator ˆc of c with the estimates ˆm
α
.
2.1 Formal Definition
Although the pre-smoother ˜m could be calculated applying any smoothing method, theory has al-
ways been derived for kernel estimators [note that the same happened to the backfitting (Opsomer
and Ruppert 1997, Mammen, Linton and Nielsen 1999)]. Therefore we will concentrate only on the
kernel based definitions even though spline implementation is known to be computationally more
advantageous. We first give the definition of the classic marginal integration method (CMIE). Let
K
i
(·)(i =1, 2) denote one - and (d −1) - dimensional Lipschitz - continuous kernels of order p and q,
respectively, with compact support, and define for a bandwidth h
i
> 0, i =1, 2, t
1
∈ IR, t
2
∈ IR
d−1
K
1,h
1
(t
1
)=
1
h
1
K
1
(
t
1
h
1
),K
2,h
2
(t
2
)=
1
h
d−1
2
K
2
(
t
2
h
2
). (2.6)
4

For the sample (X
i
, Y
i
)
n
i=1
, X
i
= (X
i1
,...,X
id
)
T
the CMIE is defined by
ˆm
α
(x
α
)=
1
n
n
j=1
˜m(x
α
,X
j,−α
)=
1
n
2
n
k=1
n
j=1
K
1,h
1
(X
jα
− x
α
)K
2,h
2
(X
j,−α
− X
k,−α
)Y
j
ˆ
f(x
α
,X
k,−α
)
(2.7)
ˆ
f(x
α
,x
−α
)=
1
n
n
i=1
K
1,h
1
(X
i,α
− x
α
)K
2,h
2
(X
i,−α
− x
−α
) (2.8)
ˆc =
1
n
n
j=1
Y
j
(2.9)
and X
i,−α
denotes the vector X
i
without the component X
iα
. Note that
ˆ
f is an estimator of the joint
density of X and ˜m denotes the Nadaraya Watson estimator with kernel K
1,h
1
· K
2,h
2
.
The modification giving us the internalized marginal integration estimate (IMIE) concerns the defini-
tion of ˆm, equation (2.7), where
ˆ
f(x
α
,X
k,−α
) is substituted by
ˆ
f(X
jα
,X
j,−α
), see Jones, Davies and
Park (1994) or Kim, Linton and Hengartner (2000) for details. The resulting definition of the IMIE is
ˆm
I
α
(x
α
)=
1
n
2
n
k=1
n
j=1
K
1,h
1
(X
jα
− x
α
)K
2,h
2
(X
j,−α
− X
k,−α
)Y
j
ˆ
f(X
jα
,X
j,−α
)
(2.10)
=
1
n
n
j=1
K
1,h
1
(X
jα
− x
α
)
ˆ
f
−α
(X
j,−α
)
ˆ
f(X
jα
,X
j,−α
)
Y
j
, (2.11)
where
ˆ
f
−α
is an estimate of the marginal density f
−α
. Notice that the fraction before Y
j
in (2.11)
is the inverse of the conditional density f
α|−α
(X
α
|X
−α
). It is well known that under the hypothesis
of an additive model ˆm
α
and ˆm
I
α
are consistent estimates of m
α
(α =1,...,d) (see Tjøstheim and
Auestad, 1994, and Kim, Linton and Hengartner, 2000).
2.2 On a Better Understanding of Marginal Integration
Although the papers of Nielsen and Linton (1997) and Sperlich, Linton and H¨ardle (1999) already
emphasized the differences of backfitting and marginal integration, often they are still interpreted as
competing estimators for the same aim. For a better understanding of the difference between orthog-
onal projection into the additive space (backfitting) and measuring the marginal impact (marginal
integration) we give two more examples.
As has been explained in Stone (1994) and Sperlich, Tjøstheim and Yang (2000), any model can be
written in the form
m(x)=c +
d
α=1
m
α
(x
α
)+
1≤α<β≤d
m
αβ
(x
α
,x
β
)+
1≤α<β<γ≤d
m
αβγ
(x
α
,x
β
,x
γ
)+··· . (2.12)
The latter mentioned article, even when they worked it out in detail only for second order interactions,
showed that all these components can be identified and consistently estimated by marginal integration
obtaining the optimal convergence rate in smoothing. The main reason for this nice property is, that
definition, algorithm and thus the numerical results for the estimates do not differ whatever the chosen
extension or the true model is. This certainly is different for an orthogonal projection. At first we note
that so far model (2.12) can not be estimated by backfitting. Secondly, Stone (1994) gives (formal)
5