




Did you find this useful? Give us your feedback








58 citations
...Other approximations of (RND) have been considered in the literature, see Poss (2013) and the references therein....
[...]
...In the next section, we apply the two versions of Algorithm 1 to the instances studied by Poss and Raack (2013)....
[...]
...The above optimization problem has been studied previously by Poss and Raack (2013). Poss and Raack (2013) solves (RND) by enumerating the extreme points of Ξ using Lemma 1....
[...]
...…polytopes having limited number of extreme points and they address larger problems by applying affine decision rules to routing variables y: yk(ξ) = f0k + ∑ h∈K fhkξh, k ∈ K. (25) Other approximations of (RND) have been considered in the literature, see Poss (2013) and the references therein....
[...]
...We assess our algorithms on a difficult telecommunication network design problem that has previously been studied in the literature by Poss and Raack (2013), comparing our results with the affine decision rules....
[...]
15 citations
...Notice that Poss (2013, 2014b) has recently pointed out the conservatism of the second probabilistic bound from Theorem 5....
[...]
...Intermediary routing schemes have also been considered, see Poss (2014a) and the references therein, among which affine routing, introduced by Ouorou and Vial (2007), stands out for offering a good balance between computational complexity and flexibility....
[...]
13 citations
...However, they lead to optimization problems that are even harder to solve than the problem with dynamic routing [43]....
[...]
7 citations
...Also one can check that opt(Faff ) ≤ opt(FVA) ≤ opt(FVG) using the same arguments of [28]....
[...]
...In [28] the author compares optimal solutions for different routing strategies F, defined as opt(F)....
[...]
...We define each routing scheme from a robust optimization perspective as in [28]....
[...]
3 citations
3,364 citations
3,359 citations
...Bertsimas and Sim [13] consider general linear programs where the coefficients of each linear inequality belong to intervals such that the number of coefficients taking conjointly their maximum value is bounded by a constant Γ....
[...]
...Similarly, if dkmin = d k max, then any routing in FVS or FVG is uniquely determined by a unique routing template for k. Suppose that 0 dkmin d k max....
[...]
...The polytope introduced by Bertsimas and Sim [13], used for robust network design problems in [6, 23, 24, 20, 26], satisfies the assumption of (b) when the number of deviations allowed is integer....
[...]
...Further works by Chen and Zhang [15] and Goh and Sim [17] suggest to extend the second stage to piece-wise linear functions of the uncertainties....
[...]
...Similarly, flow f(d2) uses the routing template y 2k = fk(dk2)/d k 2 for k = k1, k2....
[...]
1,813 citations
...In this context, a solution is said to be feasible for the problem if it is feasible for all demand vectors that belong to the estimated uncertainty set D, see Soyster [28] and Ben-Tal and Nemirovski [9, 10], among others....
[...]
1,809 citations
...This result follows directly from the dualization technique introduced by [9] for robust linear optimization....
[...]
...In this context, a solution is said to be feasible for the problem if it is feasible for all demand vectors that belong to the estimated uncertainty set D, see the seminal works of [26] and [9]....
[...]
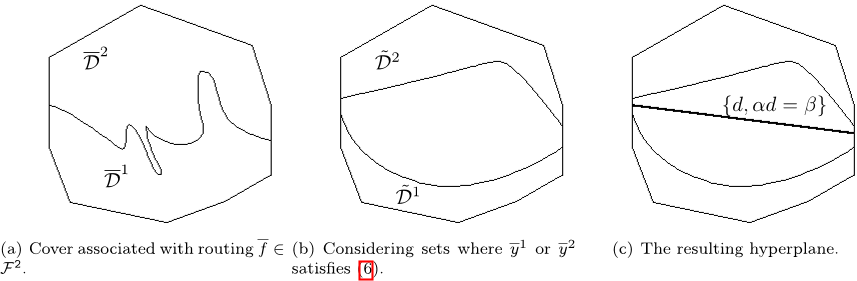
The authors show that the routing set based on an arbitrary cover of the uncertainty is equivalent to the routing set that uses a separation hyperplane. Moreover, while a finite linear programming formulation can be provided for the robust network design problem with dynamic routing under polyhedral uncertainty ( by considering only the extreme points of the demand polytope ), no such formulations are known for the problems that use the general volume routings or the routings based on covers of the uncertainty set.