FEDERAL RESERVE BANK OF S T
.
LOUIS
RE V I EW
SEPTEMBER
/
OCTO B E R
201 1 325
A Comprehensive Revision of the
U.S. Monetary Services (Divisia) Indexes
Richard G. Anderson and Barry E. Jones
The authors introduce a comprehensive revision of the Divisia monetary aggregates for the
United States published by the Federal Reserve Bank of St. Louis, referred to as the Monetary
Services Indexes (MSI). These revised MSI are available at five levels of aggregation, including a
new broad level of aggregation that includes all of the assets currently reported on the Federal
Reserve’s H.6 statistical release. Several aspects of the new MSI differ from those previously pub-
lished. One such change is that the checkable and savings deposit components of the MSI are now
adjusted for the effects of retail sweep programs, beginning in 1994. Another change is that alter-
native MSI are provided using two alternative benchmark rates. In addition, the authors have sim-
plified the procedure used to construct the own rate of return for small-denomination time deposits
and have discontinued the previous practice of applying an implicit return to some or all demand
deposits. The revised indexes begin in 1967 rather than 1960 because of data limitations.
(JEL C43, C82, E4, E50)
Federal Reserve Bank of St. Louis Review, September/October 2011, 93(5), pp. 325-59.
financial assets selected by consumers and firms
may be separated into two groups. Some assets,
including currency and checkable bank deposits,
are innately medium of exchange—that is, usable
in the purchase and sale of goods and services—
while others cannot be used until converted to
medium of exchange.
1
Generally, monetary assets
that differ in terms of their potential usefulness
as medium of exchange also differ in their own
rates of return. Barnett (1980) developed the
concept and theory of monetary index numbers,
Money is necessary to the carrying on of trade.
For where money fails, men cannot buy, and
trade stops.
—John Locke, Further Considerations
Concerning Raising the Value of Money
(1696, p. 319; quoted by Vickers, 1959)
M
oney plays a crucial role in the econ-
omy because the purchase and sale of
goods and services is settled in what
economists refer to as “medium of exchange.”
Forward-looking consumers and firms determine
their desired quantities of medium of exchange
at approximately the same time as they (i) form
expectations of future income and expenditure
and (ii) make decisions regarding desired quan-
tities of financial and nonfinancial assets. The
1
There are exceptions, of course. Bank checks, for example, are not
accepted by all merchants. Even for currency, there are exceptions
(see Twain, 1996). More seriously, currency issued by a sovereign
country often is not accepted in other countries; for a discussion
of monetary index numbers defined across currencies, see Barnett
(2007).
Richard G. Anderson is an economist and vice president at the Federal Reserve Bank of St. Louis and visiting professor, Management School,
University of Sheffield (U.K.). Barry E. Jones is associate professor of economics at Binghamton University–State University of New York. The
authors thank Yang Liu and Esha Singha for research assistance and Barry Cynamon, Livio Stracca, and Jim Swofford for helpful comments
on an earlier draft. Anderson thanks the research department of the Federal Reserve Bank of Minneapolis for their hospitality during the com-
pletion of this analysis. Jones thanks the Federal Reserve Bank of St. Louis and the department of economics at Lund University for their
hospitality during several visits.
©
2011, The Federal Reserve Bank of St. Louis. The views expressed in this article are those of the author(s) and do not necessarily reflect the
views of the Federal Reserve System, the Board of Governors, or the regional Federal Reserve Banks. Articles may be reprinted, reproduced,
published, distributed, displayed, and transmitted in their entirety if copyright notice, author name(s), and full citation are included. Abstracts,
synopses, and other derivative works may be made only with prior written permission of the Federal Reserve Bank of St. Louis.

which he referred to as “Divisia monetary aggre-
gates.” Divisia aggregates measure, in a method
consistent with intertemporal microeconomic
theory, the aggregate flow of monetary services
derived by consumers and firms from a collec-
tion of monetary assets with different character-
istics and different rates of return. Underlying
Divisia monetary aggregates is the concept of the
user cost of a monetary asset, which is a func-
tion of the interest forgone by holding a specific
asset rather than an alternative asset that does
not provide any monetary services and earns a
higher rate of return (referred to as the “bench-
mark rate”). The close connection in microeco-
nomic theory between monetary index numbers
and agents’ anticipated income and expenditure
suggests that monetary index numbers should
be more closely related to economic activity than
conventional simple sum monetary aggregates
(see, for example, Hancock, 2005; Barnett and
Chauvet, 2011; Barnett, forthcoming).
THE MACROECONOMICS OF
MONETARY AGGREGATION
This article discusses how to construct mon-
etary index numbers (Divisia monetary aggregates)
for the United States.
2
For the most part, we do
not address when or why such measurement and
aggregation might be desirable, which is contro-
versial to some extent among macroeconomists.
The extant principal body of current macroeco-
nomic analysis widely uses the concept of an
aggregate measure of money and distinctly sepa-
rates “money” from other assets, financial and
nonfinancial.
3
Typically, macroeconomists define
“money” as financial assets that either are medium
of exchange or convertible to medium of exchange
at de minimus cost. Demand for such assets is
motivated in a macroeconomic model by either
cash-in-advance or shopping-time constraints or
a money-in-the-utility (or production) function
specification.
4
Models differ, however, regarding
whether a household or firm might replenish a
depleted stock of money during the current period
by selling (or using as collateral) its nonmonetary
assets. If such a mechanism is permitted, the cor-
rect definition of a monetary aggregate for macro-
economic analysis depends on assumptions
regarding the liquidity of those assets that are not
medium of exchange.
A complementary, but alternative, line of
thought argues that (i) the concept of a monetary
aggregate in macroeconomics is unnecessary and
misleading and (ii) models should focus on the
functions of financial assets, including as a
medium of exchange and an intertemporal store
of value. Monetary aggregates, for example, have
no role in the class of recent search-based macro-
economic models that Stephen Williamson and
Randall Wright have labeled “New Monetarist
economics.”
5
Although the exchange of goods
and services is fundamental in such models, the
role of an asset as a medium of exchange is unim-
portant because the models (implicitly or explic-
itly) assume a transformation technology such
that (almost) any asset can fulfill the functional
role of medium of exchange—that is, all assets
are liquid. For example, Williamson and Wright
(2010, p. 294) write:
Note as well that theory provides no particular
rationale for adding up certain public and pri-
vate liabilities (in this case currency and bank
deposits), calling the sum money, and attach-
ing some special significance to it. Indeed,
there are equilibria in the model where cur-
rency and bank deposits are both used in some
of the same transactions, both bear the same
rate of return, and the stocks of both turn over
once each period. Thus, Friedman, if he were
alive, might think he had good reason to call
the sum of currency and bank deposits money
and proceed from there. But what the model
tells us is that public and private liquidity play
Anderson and Jones
326
SEPTEMBER
/O
CTO B E R
201 1
FEDERAL RESERV E B A N K OF ST
.
LOUIS
RE V I EW
2
Throughout this analysis, the term “monetary assets” refers to those
financial assets that can provide “monetary services” during the
period—that is, they can serve as a medium of exchange. Some
assets (currency, checkable deposits) are immediately medium
of exchange. Other assets have the standby capability to act as
medium of exchange if there exist markets that allow the assets to
be exchanged for medium of exchange when need be, either by
means of a sale or use as collateral.
3
Walsh (2010) is a comprehensive recent textbook treatment.
4
A classic analysis is King and Plosser (1984).
5
Williamson and Wright (2010, 2011).

quite different roles. In reality, many assets are
used in transactions, broadly defined, includ-
ing Treasury bills, mortgage-backed securities,
and mutual fund shares. We see no real pur-
pose in drawing some boundary between one
set of assets and another, and calling members
of one set money.
New Monetarist-style models seek to illustrate
how a demand for monetary services arises as a
result of optimizing behavior by households and
firms. To do so, generally speaking, the models
assert that a shortage of medium of exchange is
costly in the sense that trades do not occur that
otherwise would be Pareto welfare-improving.
In such models, most financial assets are treated
as near-perfect substitutes; the role of the trans-
action costs entailed in exchanging an asset that
does not furnish medium of exchange services
for one that does is secondary, such that even
mortgage-backed securities furnish medium of
exchange (that is, monetary) services.
In a related recent analysis that addresses
neither the wisdom nor the necessity of monetary
aggregation, Holmström and Tirole (2011) ask if
transaction costs and “sudden stops” in financial
markets explain why households and firms choose
to hold larger quantities of highly liquid assets
than is suggested by models with de minimus
asset-market transaction costs. They note: “While
some forms of equity, such as private equity, may
not be readily sold at a ‘fair price,’ many long-
term securities are traded on active organized
exchanges…liquidating one’s position…can be
performed quickly and at low transaction costs”
(p. 1). Their analysis implies that not all financial
assets are perfect substitutes due to the risks that
(i) market trading might suddenly halt, (ii) differ-
ential user costs can arise in the solution to the
optimization problem facing households and
firms, and (iii) such differential user costs reflect
the differing amounts of monetary services fur-
nished by the assets.
THE ROLE OF THE FEDERAL
RESERVE BANK OF ST. LOUIS
The Federal Reserve Bank of St. Louis has
published monetary index numbers (initially
referred to as Divisia monetary aggregates and,
later, as Monetary Services Indexes [MSI]) for
two decades, beginning with Thornton and Yue
(1992) and continuing with Anderson, Jones,
and Nesmith (1997a,b,c) and Anderson and Buol
(2005). Publication of the most recent series was
suspended in March 2006 when certain necessary
data became unavailable.
In this paper, we introduce a comprehensive
revision of the MSI constructed at five levels of
aggregation: MSI-M1, MSI-M2, MSI-M2M, MSI-
MZM, and MSI-ALL. MSI-M1 and MSI-M2 are
constructed, respectively, over the same compo-
nents included in the Federal Reserve Board’s
M1 and M2 monetary aggregates. MSI-ALL is con-
structed over all assets currently reported on the
Federal Reserve Board’s H.6 statistical release
(the components of M2 plus institutional money
market mutual funds [MMMFs]) and is the broad-
est level of aggregation that currently can be con-
structed from available data. Finally, MSI-M2M
and MSI-MZM are zero-maturity indexes (i.e.,
they exclude small-denomination time deposits).
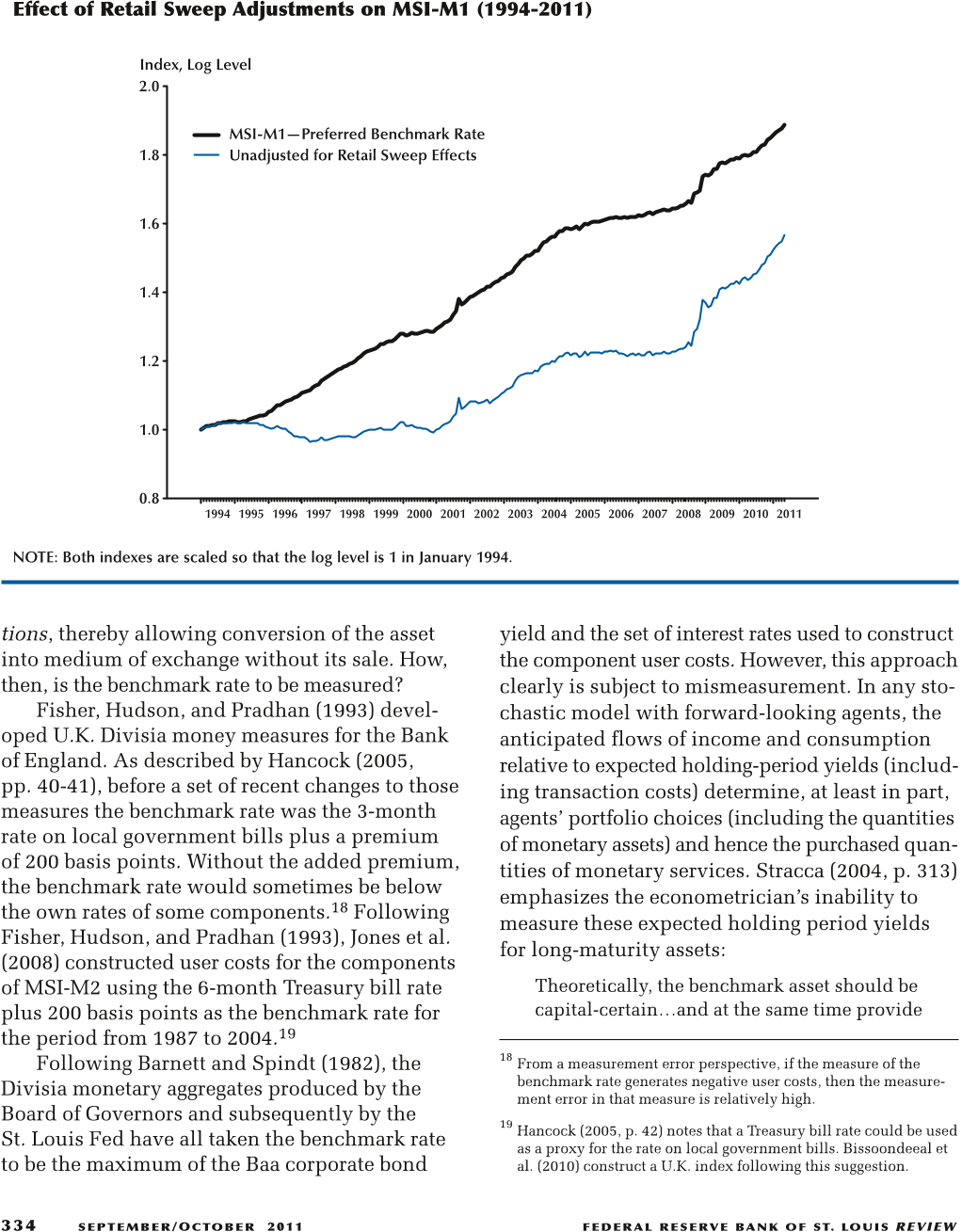
One change to the indexes is the adjustment of
checkable and savings deposit components of
the MSI for the effects of retail sweep programs,
beginning in 1994.
Several changes have been made to the user
costs of the components. Among these, we dis-
continued the previous practice of assigning an
implicit return to some or all demand deposits
and simplified the procedure used to construct
the own rate for small-denomination time deposits.
We also improved measures of savings and small
time deposit rates in the Regulation Q era; as a
consequence, the start date of the MSI has been
changed from 1960 to 1967. Finally, the MSI are
now constructed using two different benchmark
rates. Our preferred benchmark rate is the maxi-
mum taken over the own rates of the components
of MSI-ALL and a set of short-term money market
rates (referred to in the literature as the “upper
envelope”) plus a small liquidity premium. The
alternative benchmark rate is the larger of our
preferred benchmark rate and the Baa bond yield.
Previous practice had been to simply include the
Baa bond yield in the upper envelope.
The remainder of the paper is organized as
follows. The next section provides a brief over -
Anderson and Jones
FEDERAL RESERV E B A N K OF ST
.
LOUIS
RE V I EW
SEPTEMBER
/
OCTO B E R
201 1 327

view of the theory behind the MSI. We then
describe the MSI and their changes relative to
Anderson, Jones, and Nesmith (1997c). Next, we
examine the empirical properties of the MSI,
emphasizing the time-series behavior of the
indexes. The final section offers some conclusions.
MONETARY AGGREGATION AND
INDEX NUMBER THEORY
This section briefly reviews the economic
theory of monetary aggregation. Readers interested
primarily in the data may skip this section with-
out loss of continuity; readers seeking a more
comprehensive survey might consult Anderson,
Jones, and Nesmith (1997b).
The user cost of a monetary asset, defined as
the interest income forgone by holding a specific
financial asset rather than a higher-yielding asset
that does not provide monetary services, plays
an essential role in monetary aggregation theory.
Divisia monetary aggregates are chain-weighted
superlative indexes constructed over the quanti-
ties and user costs of selected sets of monetary
assets. The earliest Divisia aggregates for the
United States were constructed at the Federal
Reserve Board through the mid-1980s by Barnett,
Offenbacher, and Spindt (1981) and, later, by Farr
and Johnson (1985), who introduced the descrip-
tive label “Monetary Services Indexes.”
6
Background
Barnett (1978, 1980) developed Divisia mone-
tary aggregates from aggregation and index num-
ber theory; see Barnett and Serletis (2000) for a
comprehensive overview. The basic ideas can be
illustrated with a simple money-in-the-utility
function model. In each period t, a representative
consumer is assumed to maximize lifetime utility:
where c
s
denotes a vector of quantities of a set of
nonmonetary goods and services and m
s
denotes
β
s t
s t
s s
u
−
=
∞
∑
( )
c m, ,
a vector of real stocks of a set of monetary assets.
The budget constraints are given by
for all s ≥ t, where b
s
denotes the real stock of a
benchmark asset that does not enter into the util-
ity function, Y
s
represents nominal income not
due to asset holdings, p
*
s
is a price index used to
convert nominal stocks to real terms, p
s
is the
price vector for the nonmonetary goods and serv-
ices, R
s
is the nominal rate of return on the bench-
mark asset, and r
n
,s
is the nominal own rate of
return (possibly zero) for the nth monetary asset.
The user cost of each monetary asset is
derived from the above maximization. Barnett
(1978) derived the formula for the user cost of a
monetary asset by combining individual-period
budget constraints into a single lifetime budget
constraint. When optimizing in period t, current-
period real money balances, m
n,t
, are multiplied
in the lifetime budget constraint by
π
n,t
= p
*
t
u
n,t
,
where
Consequently,
π
n,t
is the user cost for m
n,t
.
7
Usually,
π
n,t
is referred to as the “nominal user
cost” and u
n,t
as the corresponding “real user cost”
(Barnett, 1987, p. 118). In an alternative derivation,
Donovan (1978, pp. 682-86) obtained the same
expression by applying the user cost formula
for a durable good to interest-bearing monetary
assets.
8
Diewert (1974, p. 510) did the same for
non-interest-bearing assets.
p c
s
s s s s s s
s n s n s
p b R p b
p m r
⋅ = +
( )
−
+ +
( )
−
−
− −
1
1
1 1
1
1
*
*
*
, ,
−−
+
=
∑
p m Y
s n s
n
N
s
*
,
1
u
R r
R
n t
t n t
t
,
,
.=
−
+1
Anderson and Jones
328
SEPTEMBER
/O
CTO B E R
201 1
FEDERAL RESERV E B A N K OF ST
.
LOUIS
RE V I EW
6
Divisia money measures for the United Kingdom have been main-
tained by the Bank of England since the early 1990s (see Fisher,
Hudson, and Pradhan, 1993, and Hancock, 2005).
7
More generally, when optimizing in period t, the (discounted)
user cost for m
n,s
共s ≥ t+1兲 is given by
See Barnett (1978) for further discussion. Diewert (1974) provides
analogous expressions for durable goods.
8
The user cost of a durable good is the difference between the pur-
chase price of a unit of the good and the present value of the sale
price one period later (adjusted for depreciation). Donovan’s argu-
ment is as follows: Holding p
*
t
dollars of a monetary asset in period
t is equivalent to holding one real dollar of the monetary asset.
p
R r
R R R
s
s n s
t t s
*
−
+
( )
+
( )
+
( )
+
,
.
1 1 1
1

A key property in aggregation and index
number theory is weak separability. In the present
context, monetary assets are weakly separable
from the other goods and services included in
the utility function if
where U is strictly increasing in V (see Varian,
1983, p. 104). Under weak separability, utility
maximization in period t implies that the vector
of real money balances, m
t
, chosen in that period
maximizes the sub-utility function, V共m兲, subject
to the budget constraint, π
t
.
m = π
t
.
m
t
, where π
t
is a vector of nominal user costs.
9
Chain-weighted superlative indexes con-
structed from data on the quantities of monetary
assets and their user costs can be used to measure
how V共m
t
兲 evolves over time; here, we provide
an overview (see the appendix for details). Specifi -
cally, the MSI are based on the superlative
Törnqvist-Theil formula. The chain-weighted
Törnqvist-Theil monetary quantity index is
where
is the expenditure share for the nth monetary
asset for period t. The index has the attractive
property that its log difference is a weighted aver-
age of the log differences of its components:
u U Vc m c m, , ,
( )
≡
( )
V V
m
m
t t
n t
n t
n
N
w w
n t n t
=
∏
−
−
=
+
−
1
1
1
2
1
,
,
, ,
,
w
m
m
n t
n t n t
i t i t
i
N
,
, ,
, ,
=
=
∑
π
π
1
Barnett (1980) interpreted the Törnqvist-Theil
index as a discrete-time approximation of the
continuous-time Divisia index, which is the origin
of the term Divisia monetary aggregate. As he
emphasized, in continuous time the Divisia index
is exact for any linearly homogeneous utility
function.
10
The MSI and Their Dual User Cost
Indexes
The published St. Louis MSI are constructed
from nominal rather than real monetary asset
quantities and, in that sense, are nominal mone-
tary index numbers; corresponding real MSI can
be obtained by dividing the nominal MSI by a
price index. We also publish real user cost indexes
for the various MSI that are suitable for use in
empirical work as the opportunity costs of those
MSI. The real user cost indexes can be multiplied
by a price index to obtain corresponding nominal
user cost indexes. This is analogous to the rela-
tionship between real and nominal user costs of
individual monetary assets as discussed above.
Specifically, let p
t
*
denote a price index, and
let M
n,t
and m
n,t
denote the nominal and real
quantities, respectively, of the nth monetary
asset—that is, m
n,t
= M
n,t
/p
t
*
. Let u
n,t
be the corre-
sponding real user cost, which does not depend
on the price index. The corresponding nominal
user cost is
π
n,t
=p
t
*
u
n,t
. The published nominal
MSI are constructed using nominal monetary
asset quantities as follows:
ln ln
ln
,
,
,
V V
w w
m
t t
n
t n t
n
N
n
t
( )
−
( )
=
+
( )
−
−
=
∑
1
1
1
2
−−
( )
−
ln .
,
m
n
t 1
MSI MSI
M
M
t t
n t
n t
n
N
w w
n t n t
=
−
−
=
+
∏
−
1
1
1
2
1
,
,
, ,
.
Anderson and Jones
FEDERAL RESERV E B A N K OF ST
.
LOUIS
RE V I EW
SEPTEMBER
/
OCTO B E R
201 1 329
Thus, the purchase price of a real dollar of the monetary asset is
p
*
t
and the sale price of a real dollar of the asset one period later is
p
*
t+1
. If the asset earns interest, holding p
*
t
dollars of the asset for
one period results in p
*
t
共1 + r
n,t
兲/p
*
t+1
real dollars of the asset one
period later. Consequently, the user cost of the monetary asset is
9
Barnett (1982) emphasizes weak separability in choosing the
components of a monetary aggregate. Varian (1982, 1983) derived
necessary and sufficient conditions for a dataset to be consistent
with utility maximization and weak separability. A number of
studies have applied tests of these conditions to determine if spe-
cific groupings of monetary assets are weakly separable. For recent
examples, see Jones, Dutkowsky and Elger (2005), Drake and
Fleissig (2006), and Elger et al. (2008).
p p
p r
p R
p
R r
R
t t
t n t
t t
t
t n t
t
* *
*
*
*
−
+
( )
+
( )
=
−
+
=
+
+
1
1
1
1
1
,
,
ππ
n t,
.
10
If m
t
maximizes V共m兲 subject to the budget constraint π
t
.
m =
π
t
.
m
t
for all t and V共m兲 is linearly homogeneous, then in the
continuous-time case
which corresponds to the continuous-time Divisia quantity index
(see Barnett, 1987, p. 141).
d V
dt
d V
dt
w
d m
dt
t
t
n t
n
N
n t
ln
ln
ln
,
,
( )
=
( )
( )
=
( )
=
∑
m
,
1