A Control Lyapunov Perspective on Episodic Learning
via Projection to State Stability
Andrew J. Taylor
1
, Victor D. Dorobantu
1
, Meera Krishnamoorthy,
Hoang M. Le, Yisong Yue, and Aaron D. Ames
Abstract— The goal of this paper is to understand the impact
of learning on control synthesis from a Lyapunov function
perspective. In particular, rather than consider uncertainties in
the full system dynamics, we employ Control Lyapunov Func-
tions (CLFs) as low-dimensional projections. To understand
and characterize the uncertainty that these projected dynamics
introduce in the system, we introduce a new notion: Projection
to State Stability (PSS). PSS can be viewed as a variant of Input
to State Stability defined on projected dynamics, and enables
characterizing robustness of a CLF with respect to the data used
to learn system uncertainties. We use PSS to bound uncertainty
in affine control, and demonstrate that a practical episodic
learning approach can use PSS to characterize uncertainty in
the CLF for robust control synthesis.
I. INTRODUCTION
Properly characterizing uncertainty is a key aspect of
robust control [35]. With the increasing use of learning for
dynamics modelling and control synthesis [6], [11], [9], [12],
[4], [31], [25], it is correspondingly important to develop
new tools to reason about the interplay between learning and
robust control.
In this paper, we focus on the interplay between learning
and robustness for control synthesis using Control Lyapunov
Functions (CLFs) [5], [19]. The use of CLFs has seen
multiple applications in recent years [20], [15], [24], and one
of their primary benefits is to enable control objectives to be
represented in a low-dimensional form that can be integrated
with optimization methods to yield optimal controllers [3].
This low-dimensional form is also appealing from a learning
perspective, as learning is typically more tractable in lower-
dimensional spaces [32], [34], [31].
The practical design of CLFs remains challenging. In
many cases, extensive tuning upon deployment is necessary
[20], and even with this tuning the system is often not able to
track a desired state or trajectory perfectly. Other approaches,
such as those based on adaptive control [18], can adaptively
learn a CLF but are restricted to learning over specific classes
of model uncertainty.
We thus build upon ideas in robust control in order
to guarantee performance in the presence of model mis-
specification. The idea of robust CLFs is not new (cf. [14],
*This work was supported by Google Brain Robotics and DARPA Award
HR00111890035
1
Both authors contributed equally.
All authors are with the Department of Computing and Mathematical
Sciences, California Institute of Technology, Pasadena, CA 91125, USA
ajtaylor@caltech.edu, vdoroban@caltech.edu,
mkrishna@caltech.edu, hmle@caltech.edu,
yyue@caltech.edu, ames@caltech.edu
[13]), but existing analyses focus on the full-dimensional
state dynamics, which can be burdensome for learning.
In this paper, we make two main contributions. First, we
propose a novel characterization called Projection to State
Stability (PSS), which is a variant of the well-studied Input
to State Stability (ISS) property [26], [29], [28], [33], [27],
but defined on projected dynamics rather than the original
state dynamics. Like ISS, PSS provides a tool to characterize
tracking error in terms of the magnitude of the disturbance
or uncertainty. Unlike ISS, PSS can characterize dynamic
uncertainty directly in the derivative of a CLF, thus allowing
a low dimensional representation of the uncertainty. In our
second contribution, we demonstrate the practicality of PSS
by incorporating it into an episodic learning algorithm.
Our paper is organized as follows. Section II reviews CLFs
and ISS. Section III defines Projection to State Stability
(PSS), and how PSS enables constructing bounds on the
state of a system that depend on a projected disturbance.
Section IV defines a broad class of model uncertainty for
affine control systems, evaluates how this uncertainty impacts
the Lyapunov derivative, and demonstrates how to restrict
this uncertainty with data to determine if a system is PSS.
Section V discusses how episodic learning can be used to
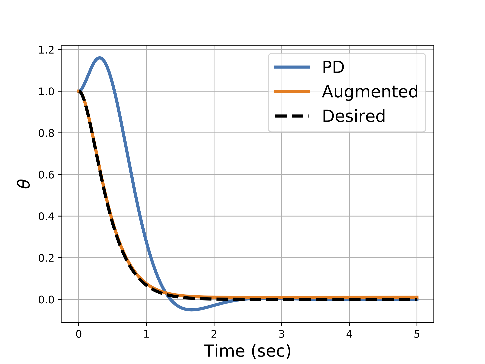
improve PSS guarantees in practice, and presents simulation
results with an uncertain inverted pendulum model.
II. PRELIMINARIES
This section provides a review of Control Lyapunov
Functions (CLFs) and Input to State Stability (ISS). These
tools will be used in Section III to define Projection to
State Stability. This section concludes with a brief discussion
of how these definitions must be modified to hold over a
restriction of the domain.
Consider a state space X ⊆ R
n
and a control input space
U ⊆ R
m
. Assume that X is path-connected and that 0 ∈ X .
Consider a system governed by:
˙
x = f (x, u), (1)
for state x ∈ X and its derivative
˙
x, control input u ∈ U,
and dynamics f : X × U → R
n
. In this paper we assume
f is locally Lipschitz continuous. The following definitions,
taken from [17], are useful in analyzing stability of (1).
Definition 1 (Class K Function). A continuous function α :
[0, a) → R
+
, with a > 0, is class K, denoted α ∈ K, if it is
monotonically (strictly) increasing and satisfies α(0) = 0. If
the domain of α is all of R
+
and lim
r→∞
α(r) = ∞, then
α is termed radially unbounded and class K
∞
.
arXiv:1903.07214v1 [cs.SY] 18 Mar 2019

Definition 2 (Class KL Function). A continuous function
β : [0, a) × R
+
→ R
+
, with a > 0, is class KL, denoted
β ∈ KL, if the function r 7→ β(r, s) ∈ K for all s ∈ R
+
,
and the function s 7→ β(r, s) is monotonically non-increasing
with β(r, s) → 0 as s → ∞ for all r ∈ [0, a).
We note that the strictly increasing nature of Class K
(K
∞
) functions permits an inverse Class K (K
∞
) function
α
−1
: [0, α(a)) → R
+
. We also note that the composition
of Class K (K
∞
) functions is itself a Class K (K
∞
) func-
tion. Given these definitions, we define Control Lyapunov
Functions (CLFs) as in [5], [19].
Definition 3 (Control Lyapunov Function). A continuously
differentiable function V : X → R
+
is a CLF for (1) on X
if there exist α, α, α ∈ K
∞
such that:
α(kxk) ≤ V (x) ≤ α(kxk)
inf
u∈U
˙
V (x, u) ≤ −α(kxk), (2)
for all x ∈ X .
If there exists a CLF for a system, then a state-feedback
controller k : X → U can be selected such that 0 is
a globally asymptotically stable equilibrium point. In par-
ticular, for all x ∈ X , k(x) should be chosen such that
˙
V (x, k(x)) ≤ −α(kxk). We note that α, α, α only need to
be Class K for this definition, but we extend them to K
∞
to
simplify later analysis.
To accommodate disturbances or uncertainties, we con-
sider a disturbance space D ⊆ R
d
, and a modified system:
˙
x = f (x, u, d), (3)
for disturbance d ∈ D and dynamics f : X × U × D → R
n
.
We again assume f is locally Lipschitz continuous. The
disturbance may be time-varying, state-dependent, and/or
input-dependent. We assume that the disturbance is bounded
for almost all times t ≥ 0 (essentially bounded in time). This
leads to the definition of ISS and ISS-CLFs as formulated
in [26], [29].
Definition 4 (Input to State Stability). Given a state-feedback
controller k : X → U, a system is Input to State Stable (ISS)
if there exist β ∈ KL
∞
and γ ∈ K
∞
such that the solution
to (3) satisfies:
kx(t)k ≤ β(kx(0)k , t) + γ
sup
τ ≥0
kd(τ)k
, (4)
for all t ≥ 0.
Definition 5 (Input to State Stable Control Lyapunov Func-
tion). A continuously differentiable function V : X → R
+
is an Input to State Stable Control Lyapunov Function (ISS-
CLF) for (3) on X if there exist α, α, α, ρ ∈ K
∞
such that:
α(kxk) ≤ V (x) ≤ α(kxk)
kxk ≥ ρ(kdk) =⇒ inf
u∈U
˙
V (x, u, d) ≤ −α(kxk), (5)
for all x ∈ X and d ∈ D.
As with CLFs, if there exists an ISS-CLF for a system,
then a state-feedback controller k : X → U can be
chosen such that the system is ISS. If the disturbance is
input-dependent, it is additionally required that k induces
essentially bounded disturbances in time.
The condition on the Lyapunov function derivative in (2)
or (5) may not be satisfied on the entire state space X .
In particular it may only be satisfied on a subset C ⊆ X .
The system may leave C during its evolution, implying the
desired derivative condition may no longer be satisfiable. We
therefore consider the following definition and lemma.
Definition 6 (Forward Invariance). Consider the system
governed by (1). A subset F ⊆ X is forward invariant if
there exists a state-feedback controller k : X → U such that
x(0) ∈ F implies x(t) ∈ F for all t ≥ 0.
The definition of forward invariance applies to systems
governed by (3), with disturbances appropriately restricted
to subsets of D if the disturbances are modeled as state-
dependent and/or input-dependent. If 0 ∈ C, we may restrict
Definitions 3 and 5 to a forward invariant subset F ⊆ C with
0 ∈ F, provided such a subset exists.
Lemma 1. A sublevel set Ω ⊆ X of an ISS-CLF V is a
forward invariant set, provided kxk ≥ ρ(kdk) for all x ∈ ∂Ω
and appropriately restricted d ∈ D.
Proof. The condition on the Lyapunov derivative in (5)
implies the existence of a state-feedback controller k : X →
U satisfying
˙
V (x, k(x), d) ≤ −α(kxk) for all x ∈ ∂Ω
and appropriately restricted d ∈ D. Let c = V (x) for any
x ∈ ∂Ω. If V (x(0)) ∈ [0, c], then V (x(t)) ∈ [0, c] for all
t > 0 by Nagumo’s Theorem [23], [1]. Thus, if x(0) ∈ Ω,
then x(t) ∈ Ω for all t ≥ 0.
III. PROJECTION TO STATE STABILITY
Input to State Stability (ISS) requires a bound on the
state in terms of the norm of the disturbance as it appears
in the state dynamics (see Definition 4 in Section II). This
requirement does not easily permit analysis of Input to State
behavior when the disturbance is more easily described by
its impact in a Lyapunov function derivative. This limitation
motivates Projection to State Stability (PSS), which instead
relies a bound on the state in terms of a projection of the
disturbance.
Definition 7 (Dynamic Projection). A continuously differ-
entiable function Π : X → R
k
is a dynamic projection if
there exist σ, σ ∈ K
∞
satisfying:
σ(kxk) ≤ kΠ(x)k ≤ σ(kxk), (6)
for all x ∈ X .
Let Y = range(Π), and let y = Π(x) for all x ∈
X . Consider the system governed by (3). The associated
projected system is governed by the dynamics:
˙
y = D
Π
(x)f(x, u, 0) + D
Π
(x)(f(x, u, d) − f (x, u, 0))
| {z }
δ
,
(7)

where D
Π
: X → R
k×n
denotes the Jacobian of Π, and
δ is implicitly a function of x, u, and d. For the following
definitions, we assume δ is essentially bounded in time.
We are now ready to state our main definition. The key
difference between PSS and ISS (Definition 4) is the use of
δ (7) rather than the native disturbance d.
Definition 8 (Projection to State Stability). Given a state-
feedback controller k : X → U, a system is Projection to
State Stable (PSS) with respect to the projection Π if there
exist β ∈ KL
∞
and γ ∈ K
∞
such that the solution to (3)
satisfies:
kx(t)k ≤ β(kx(0)k , t) + γ
sup
τ ≥0
k δ(τ) k
, (8)
for all t ≥ 0, with δ as defined in (7).
Remark 1. If Π is an inclusion map with k = n, and the
system can be specified as:
f(x, u, d) = f (x, u, 0) + d, (9)
then PSS is equivalent to ISS.
Similarly, we can also construct a Lyapunov function that
certifies a system is PSS with respect to a projection.
Definition 9 (Projection to State Stable Control Lyapunov
Function). A continuously differentiable function W : Y →
R
+
is a Projection to State Stable Control Lyapunov Function
(PSS-CLF) for (7) on X if there exist α, α, α, ρ ∈ K
∞
satisfying:
α(kΠ(x)k) ≤ W (Π(x)) ≤ α(kΠ(x)k)
kΠ(x)k ≥ ρ(kδk) =⇒ inf
u∈U
˙
W (x, u, δ) ≤ −α(kΠ(x)k),
(10)
for all x ∈ X .
As with ISS-CLFs, this definition can be restricted to a
forward invariant set containing 0. We now show that a PSS-
CLF certifies a system is PSS.
Theorem 1. If the system governed by (7) has a PSS-CLF,
then the system governed by (3) is PSS with respect to the
projection Π.
Proof. The bounds in (10) can be weakened to:
W (Π(x)) ≥ α ◦ ρ(kδk)
=⇒ inf
u∈U
˙
W (x, u, δ) ≤ −α ◦ α
−1
(W (Π(x))). (11)
That is, if (11) holds, (10) holds. Therefore, a choice of state-
feedback controller exists such that the system governed by
(7) is Input to State Stable (ISS) with δ viewed a disturbance.
This implies that there exist β ∈ KL
∞
and γ ∈ K
∞
such
that:
kΠ(x(t))k ≤ β(kΠ(x(0))k , t) + γ
sup
τ ≥0
kδ(τ)k
, (12)
for all t ≥ 0. Since Π satisfies (6) we have:
kx(t)k ≤ σ
−1
β(σ(kx(0)k), t) + γ
sup
τ ≥0
kδ(τ)k
.
(13)
Finally, define β
0
∈ KL
∞
and γ
0
∈ K
∞
as:
β
0
(r, s) = σ
−1
(2β(σ(r), s)) (14)
γ
0
(r) = σ
−1
(2γ(r)). (15)
From the weak form of the triangle inequality presented in
[26], [16], it follows that:
kx(t)k ≤ β
0
(kx(0)k , t) + γ
0
sup
τ ≥0
kδ(τ)k
. (16)
We next show that a CLF V for the undisturbed dynamics
of a system can be viewed as a projection, thus yielding a
PSS-CLF that certifies PSS with respect to V .
Corollary 1. Suppose V : X → R
+
is a CLF on X for the
system
˙
x = f(x, u, 0). Then the disturbed system governed
by (3) is PSS with respect to the projection V .
Proof. With the projection V we have that:
δ = ∇V (x)
>
(f(x, u, d) − f (x, u, 0)). (17)
where ∇V : X → R
n
is the gradient of the Lyapunov
function. The projected system is governed by:
˙
V (x, u, δ) = ∇V (x)
>
f(x, u, 0) + δ, (18)
Since V is a CLF, there exists a state-feedback controller
k : X → U satisfying:
˙
V (x, k(x), 0) ≤ −α(kxk), (19)
for all x ∈ X . Let α
p
, α
q
∈ K
∞
satisfy α
p
+ α
q
= α. Then:
˙
V (x, k(x), δ) ≤ −α(kxk) + δ
≤ −α
p
(kxk) − α
q
(kxk) + |δ|. (20)
Therefore:
kxk ≥ α
−1
q
(|δ|) =⇒
˙
V (x, k(x), δ) ≤ −α
p
(kxk). (21)
Since V is a CLF we may weaken the bounds as in the proof
of Theorem 1 to:
V (x) ≥ α ◦ α
−1
q
(|δ|)
=⇒
˙
V (x, k(x), δ) ≤ −α
p
◦ α
−1
(V (x)), (22)
noting that α ◦ α
−1
q
and α
p
◦ α
−1
are class K
∞
. It follows
from Definition 9 that the identity map on R
+
is a PSS-CLF
for (18). Therefore, the system (3) is PSS with respect to the
projection V by Theorem 1.
IV. UNCERTAINTY MODELING & ANALYSIS
In this section we consider a structured form of uncertainty
present in affine control systems. We analyze the impact of
this uncertainty on a Lyapunov function derivative, and on
the PSS behavior of the system.

A. Uncertain Affine Systems
We consider affine control systems of the form:
˙
x = f (x) + g(x)u, (23)
with drift dynamics f : X → R
n
and actuation matrix g :
X → R
n×m
. If f and g are unknown, we may consider an
estimated model of the system:
˙
x =
ˆ
f(x) +
ˆ
g(x)u, (24)
where
ˆ
f : X → R
n
and
ˆ
g : X → R
n×m
are estimates of f
and g, respectively. In this case, (23) can be expressed as:
˙
x =
ˆ
f(x) +
ˆ
g(x)u +
d
z }| {
(g(x) −
ˆ
g(x)
| {z }
A(x)
)u + f (x) −
ˆ
f(x)
| {z }
b(x)
, (25)
obtaining a representation of the dynamics as in (9). Note that
the disturbance d = A(x)u+b(x) is explicitly characterized
as time-invariant, state-dependent, and input-dependent, with
potentially unknown A(x) and b(x) for all x ∈ X .
As discussed in [2], [31], CLFs may be constructively
formed for affine systems under proper assumptions regard-
ing relative degree and unbounded control. Furthermore, if
the true system satisfies the relative degree properties of
the estimated model, then the CLF found for the estimated
system can be used for the true system.
Assume f , g,
ˆ
f, and
ˆ
g are Lipschitz continuous (implying
A and b are Lipschitz continuous), and let V be a CLF
candidate for (24). The time derivative of V is given by:
˙
V (x, u, d) =
ˆ
˙
V (x,u)
z }| {
(
ˆ
f(x) +
ˆ
g(x)u)
>
∇V (x)
+ (A(x)
>
∇V (x)
| {z }
a(x)
)
>
u + b(x)
>
∇V (x)
| {z }
b(x)
, (26)
for all x ∈ X and u ∈ U. As proposed in [31], we may
wish to reduce the estimation error |
˙
V −
ˆ
˙
V | by improving
ˆ
˙
V with estimates of a and b. Given continuous estimators
ˆ
a : X → R
m
and
ˆ
b : X → R, (26) may be reformulated as:
˙
V (x, u, d) =
ˆ
˙
V (x,u)
z }| {
(
ˆ
f(x) +
ˆ
g(x)u)
>
∇V (x) +
ˆ
a(x)
>
u +
ˆ
b(x)
+ (A(x)
>
∇V (x) −
ˆ
a(x)
| {z }
a(x)
)
>
u + b(x)
>
∇V (x) −
ˆ
b(x)
| {z }
b(x)
,
(27)
for all x ∈ X and u ∈ U.
Both formulations decompose
˙
V into an estimated com-
ponent,
ˆ
˙
V , and a residual component. In (26) the residual
terms a and b capture the effect of the unmodeled dynamics
on the Lyapunov function derivative. In (27) the residual
terms reflect the error in estimating this effect. Additionally,
viewing V as a projection results in δ = a(x)
>
u + b(x).
B. Projection to State Stability via Uncertainty Functions
If knowledge on what values a and b can assume is
available, the impact on the Lyapunov derivative can be
constrained in a manner permitting PSS analysis of a system.
Therefore, we define a function characterizing the possible
uncertainties at a given state.
Definition 10 (Uncertainty Function). Let P(R
m
× R)
denote the set of all subsets of R
m
× R. An uncertainty
function for (26) or (27) is a function ∆ : X → P(R
m
× R)
with ∆(x) bounded and satisfying (a(x), b(x)) ∈ ∆(x) for
all x ∈ X .
For a given x ∈ X , we refer to ∆(x) as an uncertainty
set. Suppose there exists a valid uncertainty function ∆ for
(26) or (27). Then V satisfies:
˙
V (x, u, δ) ≤
ˆ
˙
V (x, u) + sup
(a,b)∈∆(x)
(a
>
u + b), (28)
for all x ∈ X and u ∈ U. One major challenge is to define a
∆ that is non-vacuous and thus practically relevant. From this
point forward we limit our attention to a subset of the state
space and make a critical assumption regarding the estimate
ˆ
˙
V for a CLF V .
Assumption 1. Let V be a CLF for the system governed by
(24) on a subset C ⊆ X with 0 ∈ C. We assume that:
inf
u∈U
ˆ
˙
V (x, u) ≤ −α(kxk). (29)
for all x ∈ C. If
ˆ
˙
V is specified as in (26), then this assumption
is satisfied by definition. If
ˆ
˙
V is specified as in (27), then
this assumption states that the addition of the estimators
ˆ
a
and
ˆ
b does not make it impossible to choose a control input
such that (29) is satisfied.
If the estimated and true system satisfy the same relative
degree property, then this assumption amounts to the addition
of estimates
ˆ
a and
ˆ
b not violating the relative degree property.
Assumption 2. Let A and b be defined as in (25), and let
C be defined as in Assumption 1. We assume A and b are
bounded on C.
If C is compact, this assumption is automatically satisfied
since A and b are assumed continuous. Under Assumption
1, the set of admissible control inputs U(x):
U(x) = {u ∈ U :
ˆ
˙
V (x, u) ≤ −α(kxk)}, (30)
is non-empty, for all x ∈ C. Then the CLF V satisfies:
α(kxk) ≤ V (x) ≤ α(kxk)
inf
u∈U(x)
˙
V (x, u, δ) − sup
(a,b)∈∆(x)
(a
>
u + b) ≤ −α(kxk),
(31)
for all x ∈ C. We now develop sufficient conditions on the
uncertainty function that certifies (25) as PSS with respect
to the CLF V (with V interpreted as a projection).

Theorem 2 (Sufficient Conditions for PSS in Affine Control
Systems). Consider the system in (25), and a CLF V for (24)
with estimated time-derivative
ˆ
˙
V as defined in (26) or (27),
satisfying Assumption 1. Let ∆ be an uncertainty function
and let k : X → U be a state-feedback controller satisfying
k(x) ∈ U(x) for all x ∈ C, with U(x) defined as in (30).
Suppose there exists α
p
, α
q
∈ K
∞
with α
p
+ α
q
= α and a
sublevel set Ω ⊆ C of V satisfying:
kxk ≥ sup
(a,b)∈∆(x)
α
−1
q
(a
>
k(x) + b), (32)
for all x ∈ ∂Ω. Then the system governed by (25) is PSS
with respect to the projection V on Ω.
Proof. First, note that:
˙
V (x, k(x), δ) − sup
(a,b)∈∆(x)
(a
>
k(x) + b) ≤ −α(kxk)
= −α
p
(kxk) − α
q
(kxk), (33)
for all x ∈ C. Since (32) holds for all x ∈ ∂Ω and α
q
is
monotonically increasing, we have:
α
q
(kxk) ≥ sup
(a,b)∈∆(x)
(a
>
k(x) + b), (34)
for all x ∈ ∂Ω. It follows that:
˙
V (x, k(x), δ) ≤ −α
p
(kxk), (35)
for all x ∈ ∂Ω. This means Ω is forward invariant, with a
proof similar to that of Lemma 1. Since V is a CLF for (24),
Corollary 1 can be restricted to Ω; that is, the system is PSS
with respect to the projection V on Ω.
We may want to study a particular set of interest E over
which the impact of the uncertainty can be bounded. For r >
0, let B
r
be the open ball around 0 of radius r, typically used
to define a ball contained in E in the subsequent analysis.
Corollary 2. Suppose there is a set E and µ ≥ 0 satisfying:
sup
(a,b)∈∆(x)
(a
>
k(x) + b) ≤ µ, (36)
for all x ∈ E. If there exists a sublevel set Ω of V such that:
B
α
−1
q
(µ)
⊆ Ω ⊆ C ∩ E, (37)
then the system is PSS with respect to the (CLF) projection V
on Ω, and the smallest sublevel set of V containing B
α
−1
q
(µ)
is asymptotically stable.
Proof. First, note that:
kxk ≥ α
−1
q
(µ) ≥ sup
(a,b)∈∆(x)
α
−1
q
(a
>
k(x) + b), (38)
for all x ∈ ∂Ω, and the system is PSS on Ω by Theorem
2. The smallest sublevel set of V containing B
α
−1
q
(µ)
is
asymptotically stable since:
kxk ≥ α
−1
q
(µ) ≥ =⇒
˙
V (x, k(x), δ) ≤ −α
p
(kxk). (39)
Improving the uncertainty set (e.g., reducing uncertainty
using learning) directly leads to larger sets for a given bound,
or tighter bounds on a given set. We state this formally in
the next result.
Corollary 3 (Uncertainty Function Improvement). Consider
uncertainty functions ∆ and ∆
0
, as well as E and µ as
defined in Corollary 2.
• Fix µ > 0 and let E
µ
be defined as:
E
µ
= {x ∈ X : sup
(a,b)∈∆(x)
(a
>
k(x) + b) ≤ µ}. (40)
• Fix E ⊆ X and let µ
E
be defined as:
µ
E
= sup
x∈E
sup
(a,b)∈∆(x)
(a
>
k(x) + b). (41)
Suppose ∆
0
(x) ⊆ ∆(x) for all x ∈ X . Then the associated
set E
0
µ
and scalar µ
0
E
satisfy E
µ
⊆ E
0
µ
and µ
0
E
≤ µ
E
.
Proof.
sup
(a,b)∈∆
0
(x)
(a
>
k(x) + b) ≤ sup
(a,b)∈∆(x)
(a
>
k(x) + b). (42)
C. Uncertainty Function Construction
We now provide a constructive method for creating an
uncertainty function from a dataset of of state and control
values generated by a system. Assume A and b are Lip-
schitz continuous with constants L
A
and L
b
, respectively.
Additionally, assume that A and b are bounded on C by
constants kAk
∞
and kbk
∞
, respectively. Consider a dataset
D ⊆ (X × U) × R consisting of data-measurement pairs
((x, u),
˙
V (x, u, δ)). Such measurements of
˙
V can be ob-
tained through numerical differentiation of computed values
of V . For notational convenience, let D
0
= {(x, u) :
((x, u),
˙
V (x, u, δ)) ∈ D}.
Proposition 1. Given a dataset D, an uncertainty function
∆ can be constructed as:
∆(x) = {(a, b) ∈ R
m
× R : ±(a
>
u
0
+ b) ≤ (x, x
0
, u
0
)
for all (x
0
, u
0
) ∈ D
0
}, (43)
for all x ∈ X , where : X × X × U → R
+
is continuous.
Remark 2. For all x ∈ X , ∆(x) is a closed, symmetric
polyhedron and is bounded given sufficiently diverse control
inputs in the dataset. In this case, ∆(x) is a compact, convex
set. The supremum present in Theorem 2 and Corollary 2
becomes a linear program (LP) and can be efficiently solved.
Proof of Proposition 1. Define observed error as:
(x, u) =
˙
V (x, u, δ) −
ˆ
˙
V (x, u)
, (44)
for all (x, u) ∈ D
0
. Consider a test point (x, u) ∈ X × U
and a data point (x
0
, u
0
) ∈ D
0
. Note that (x
0
, u
0
) satisfies:
(x
0
, u
0
) = |a(x
0
)
>
u
0
+ b(x
0
)|
= |a(x)
>
u
0
+ b(x) + (a(x
0
) − a(x))
>
u
0
+ b(x
0
) − b(x)|
≥ |a(x)
>
u
0
+ b(x)|
− ka(x
0
) − a(x)k
2
ku
0
k
2
− |b(x
0
) − b(x)|,
(45)