Q1. What are the contributions in "A convex approach to a class of non-convex building hvac control problems: illustration by two case studies" ?
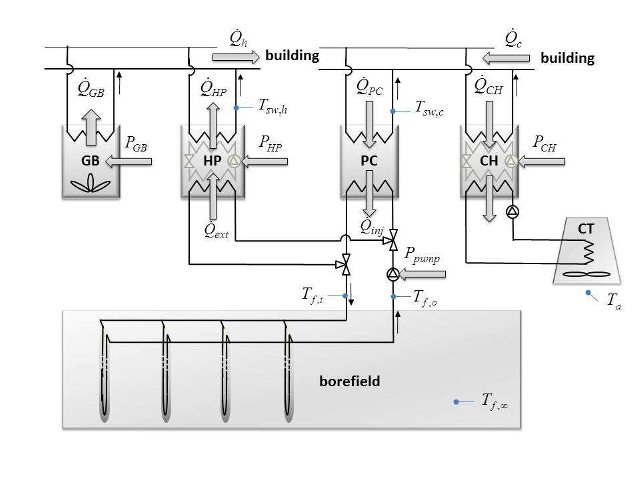
In this paper, a convexification approach is presented for a class of non-convex optimal/model predictive control problems more specifically applied to building HVAC control problems. The suggested method is especially useful for optimal building HVAC control/design problems which include non-convex bilinear or fractional terms.
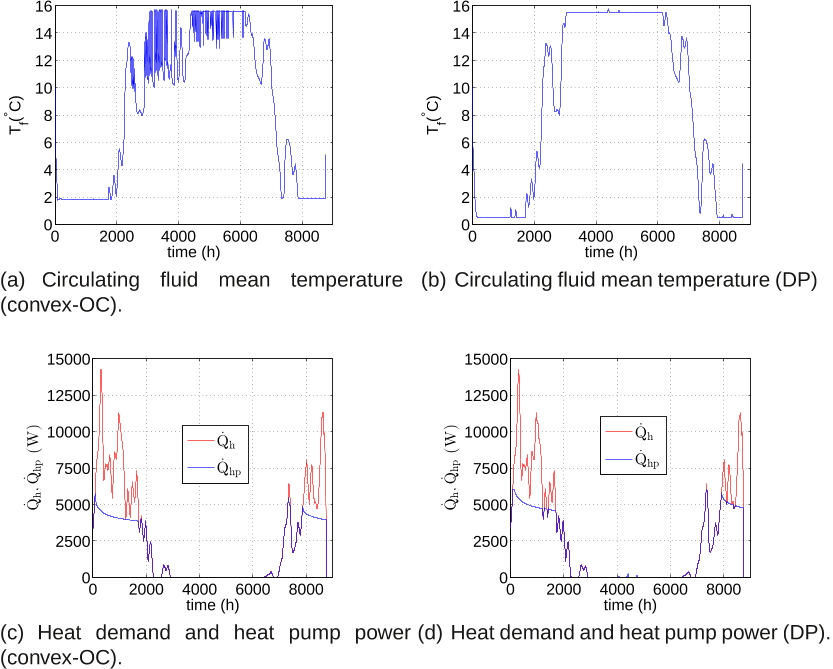

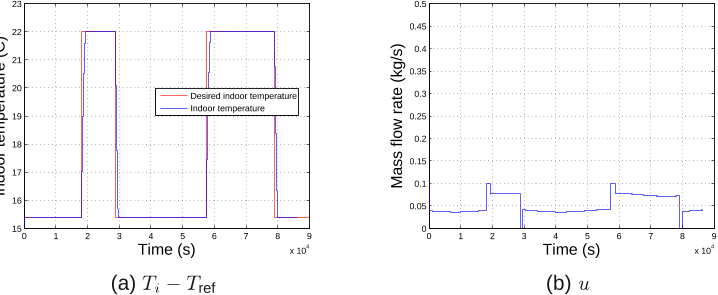
![Figure 1: Adaptive control: indoor temperature response and control input, figure taken from [19].](/figures/figure-1-adaptive-control-indoor-temperature-response-and-1jxspgpl.png)
![Figure 2: Fuzzy control: indoor temperature response and control input, figure taken from [19].](/figures/figure-2-fuzzy-control-indoor-temperature-response-and-4ad8bh4e.png)

![Table 1: Model parameters of the simulated building HVAC system [19]](/figures/table-1-model-parameters-of-the-simulated-building-hvac-24ckca9o.png)
