A different approach for calculating Franck–Condon factors
including anharmonicity
Josep M. Luis
a)
Department of Chemistry and Biochemistry, University of California, Santa Barbara, California 93106
and Department of Chemistry, University of Ottawa, Ottawa, Canada K1N 6N5
David M. Bishop
Department of Chemistry, University of Ottawa, Ottawa, Canada K1N 6N5
Bernard Kirtman
Department of Chemistry and Biochemistry, University of California, Santa Barbara, California 93106
共Received 6 August 2003; accepted 9 October 2003兲
An efficient new procedure for calculating Franck–Condon factors, based on the direct solution of
an appropriate set of simultaneous equations, is presented. Both Duschinsky rotations and
anharmonicity are included, the latter by means of second-order perturbation theory. The critical
truncation of basis set is accomplished by a build-up procedure that simultaneously removes
negligible vibrational states. A successful test is carried out on ClO
2
for which there are
experimental data and other theoretical calculations. © 2004 American Institute of Physics.
关DOI: 10.1063/1.1630566兴
I. INTRODUCTION
Along with the development of experimental high-
resolution vibronic spectroscopies, the problem of analyzing
the observed spectra is receiving increased attention. In the
Born–Oppenheimer approximation the leading term that
governs the spectral intensity pattern is given by the square
of the vibrational overlap integrals, also known as Franck–
Condon factors 共FCF’s兲, between the initial and final states.
If the vibrational normal coordinates for the two electronic
states are parallel 共i.e., if they are the same except for the
shift in equilibrium geometry兲, then these integrals will sepa-
rate in the harmonic oscillator approximation into a product
of individual oscillator terms. In general, however, this is not
the case and, discounting possible simplifications due to
symmetry, one must evaluate 3N-6 共or 3N-5 for linear mol-
ecules兲 dimensional overlap integrals. The difficulty of doing
so is compounded by the fact that the difference in equilib-
rium geometry as well as the anharmonicity of the electronic
potential-energy surfaces must be taken into account.
A variety of methods have been proposed for dealing
with this problem, particularly at the harmonic level.
1
One of
these is based on the generating function approach of Sharp
and Rosenstock,
2
which is an extension of the method intro-
duced by Hutchisson
3
for diatomics. This method has been
further developed by Chen
4
and improved by Ervin et al.
5
in their application to the naphthyl radical. Very recently,
Kikuchi et al.
6
derived a simpler form of the Sharp and
Rosenstock general formula and applied it to SO
2
in the
harmonic oscillator approximation. Another method based on
the generating function approach is due to Ruhoff
7
who de-
rived recursion relations for the calculation of multidimen-
sional FCF’s by generalizing Lerme
´
’s
8
procedure for two-
dimensional FCF’s. Also employing the generating function
method, Islampour et al. derived a closed-form multidimen-
sional harmonic oscillator expression, where the FCF’s were
expressed as sums of products of Hermite polynomials.
9
An alternative procedure, utilizing the recursion rela-
tions of Doctorov, Malkin, and Man’ko,
10
has been employed
for a variety of molecules such as phenol,
11,12
anthracene,
13
and pyrazine.
14
In addition, two different methods for calcu-
lating the FCF’s were developed by Faulkner and
Richardson.
15
The central feature of their first method is a
linear transformation of the normal coordinates in both the
ground and excited electronic states in order to effectively
remove the Duschinsky rotations
16
共i.e., the transformation
of coordinates from one electronic state to another兲. This was
originally restricted to the case where either the initial or
final vibrational wave function is the ground state, but Ku-
lander later removed this restriction.
17,18
The second method
of Faulkner and Richardson is based on a perturbation ex-
pansion of the vibrational wave functions of the excited elec-
tronic state in terms of the ground electronic state vibrational
wave functions.
15
Finally, Malmqvist and Forsberg
19
have
expressed the FCF matrix as the product of lower triangular
and upper triangular matrices which are calculated from re-
cursion formulas.
At this juncture we take note of a very different ap-
proach, developed by Segev, Heller, and co-workers,
20,21
based on considering the transitions in phase space. Those
phase-space points where the classical Wigner function for
the initial state is maximal, subject to a classical energy con-
straint on the final state, determine propensity rules for the
FCF’s. These rules, in turn, provide a way of selecting the
transitions that have substantial intensity and their FCF’s can
be estimated by subsequent phase-space integration. The
truncation of the vibrational basis is a critical aspect in re-
a兲
Permanent address: Institute of Computational Chemistry and Department
of Chemistry, University of Girona, Campus de Montilivi, 17071 Girona,
Catalonia, Spain.
JOURNAL OF CHEMICAL PHYSICS VOLUME 120, NUMBER 2 8 JANUARY 2004
8130021-9606/2004/120(2)/813/10/$22.00 © 2004 American Institute of Physics
Downloaded 31 Dec 2003 to 130.206.124.176. Redistribution subject to AIP license or copyright, see http://ojps.aip.org/jcpo/jcpcr.jsp

ducing the computational effort of any method. Our own
prescription for doing this is described in Sec. II D.
Although the procedures mentioned above can, in prin-
ciple, include vibrational anharmonicity not much attention
has been paid to this aspect. Iachello’s group has developed a
procedure based on the use of Morse oscillators in a novel
Lie algebraic scheme.
22–24
More recently Mok et al.
25
have
proposed an expansion technique that builds on the earlier
work of Botschwina and co-workers.
26
However, these meth-
ods and other approaches
27–29
to the vibrational anharmonic-
ity problem have only been applied to small molecules or to
two-dimensional model potentials.
30
Reimers has also
described
31
an approximate method for taking into account
the floppy motions of large molecules by means of curvilin-
ear coordinates.
Apart from one-photon absorption 共and emission兲 FCF’s
figure prominently in two-photon absorption 共TPA兲. The vi-
brational contribution to nonlinear optical 共NLO兲 properties,
including TPA,
32
has occupied the attention of the present
authors for some time.
33–36
As far as nonresonant NLO pro-
cesses are concerned, it is also known that mechanical and
electrical anharmonicities of ordinary 共as well as floppy兲
molecules often play a major role.
37
On the basis of very
approximate treatments
38–40
it has been suggested that the
same is true for resonant processes and in particular for TPA.
We have now begun to develop a rigorous theory for vibra-
tional effects in TPA in order to investigate that situation
more thoroughly. In the course of doing so, we have come
across a simple direct way to evaluate FCF’s and it is this
new scheme that is presented here. Effects due to: 共i兲
changes in the normal coordinates with electronic state
共Duschinsky rotations兲;
16
共ii兲 changes in the equilibrium ge-
ometry with electronic state; and 共iii兲 mechanical anharmo-
nicities in both electronic states, are all taken into account.
In the next section a general theory, which includes all of
the above effects, is formulated. Then, in Sec. III we discuss
how the resulting equations are solved along with other com-
putational details. This is followed by an example where our
method is used to simulate the He I photoelectron 共PE兲 spec-
trum of ClO
2
, in order to compare with the work of Mok
et al.
25
Finally, we conclude with a brief discussion of future
plans for incorporating this methodology into our treatment
of TPA for large conjugated molecules.
II. THEORY
The goal of this section is the derivation of a new ana-
lytical procedure to calculate the Franck–Condon factors of
polyatomic molecules taking into account both the Duschin-
sky rotations and the mechanical anharmonicity.
A. General formulation
We denote the vibrational Hamiltonian, wave functions,
and energies of the ground electronic state by H
ˆ
g
,
兩
g
g
典
, and
E
g
g
and their counterparts for an electronic excited state by
H
ˆ
e
,
兩
e
e
典
, and E
e
e
. Note that ‘‘g’’ refers to the ground elec-
tronic state and ‘‘e’’ to an excited electronic state throughout.
In either case the molecule is assumed to be nonrotating and
thus the rotational state is suppressed. Then the respective
Schro
¨
dinger equations for nuclear motion are given by
H
ˆ
g
兩
g
g
典
⫽E
g
g
兩
g
g
典
, 共1兲
H
ˆ
e
兩
e
e
典
⫽E
e
e
兩
e
e
典
. 共2兲
Multiplication of Eq. 共1兲 by
具
e
e
兩
and Eq. 共2兲 by
具
g
g
兩
leads
to
具
e
e
兩
H
ˆ
g
兩
g
g
典
⫽E
g
g
S
e
g
, 共3兲
具
g
g
兩
H
ˆ
e
兩
e
e
典
⫽E
e
e
S
g
e
, 共4兲
where S
e
g
are the Franck–Condon overlap integrals 共the
wave functions are taken to be real兲:
S
e
g
⫽S
g
e
⫽
具
e
e
兩
g
g
典
⫽
具
g
g
兩
e
e
典
. 共5兲
Subtraction of Eq. 共4兲 from Eq. 共3兲, and using the Hermitian
property of H
ˆ
g
, gives
具
g
g
兩
H
ˆ
g
⫺H
ˆ
e
兩
e
e
典
⫽
共
E
g
g
⫺E
e
e
兲
S
g
e
. 共6兲
Since the vibrational eigenfunctions for the excited elec-
tronic state (
e
e
below兲 form a complete set, the left-hand
side of Eq. 共6兲 can be expressed as
具
g
g
兩
H
ˆ
g
⫺H
ˆ
e
兩
e
e
典
⫽
兺
e
具
g
g
兩
e
e
典具
e
e
兩
H
ˆ
g
⫺H
ˆ
e
兩
e
e
典
⫽
兺
e
S
g
e
具
e
e
兩
H
ˆ
g
⫺H
ˆ
e
兩
e
e
典
. 共7兲
Equation 共7兲 contains the entire set of Franck–Condon over-
laps between the initial vibrational wave function of the
ground electronic state and all final vibrational wave func-
tions of the excited electronic state. This allows us to solve
for the entire set of overlap integrals in which we are inter-
ested simultaneously. If the vibrational wave functions of the
electronic excited state had been expanded in terms of the
electronic ground-state vibrational wave functions, then only
one of the desired overlaps would be obtained and the pro-
cess would have to be repeated for each final state. In either
event the properties of both the ground and excited electronic
states are necessary for the calculations.
Combining Eqs. 共6兲 and 共7兲, while taking into account
the fact that the total nuclear kinetic energy operator is the
same in both Hamiltonians (H
ˆ
g
⫽T
ˆ
⫹V
ˆ
g
, H
ˆ
e
⫽T
ˆ
⫹V
ˆ
e
), one
obtains
兺
e
S
g
e
关
具
e
e
兩
V
ˆ
g
⫺V
ˆ
e
兩
e
e
典
⫹
共
E
e
e
⫺E
g
g
兲
␦
e
e
兴
⫽0, ᭙
e
, and ᭙
g
, 共8兲
where
␦
e
e
is the Kronecker delta.
For a given
g
, Eq. 共8兲 constitutes an infinite set of
homogeneous simultaneous linear equations with an infinite
number of unknowns S
g
e
共all
e
). The first step in solving
this set of equations is to truncate to a finite set of
e
and
e
values. The details of the systematic iterative algorithm used
814 J. Chem. Phys., Vol. 120, No. 2, 8 January 2004 Luis, Bishop, and Kirtman
Downloaded 31 Dec 2003 to 130.206.124.176. Redistribution subject to AIP license or copyright, see http://ojps.aip.org/jcpo/jcpcr.jsp

to select the M equations that survive the truncation are
given in the next section. Then after dividing by S
g
e
(
e
is
arbitrary as long as S
g
e
⫽0),
兺
e
M
r
e
e
关
具
e
e
兩
V
ˆ
g
⫺V
ˆ
e
兩
e
e
典
⫹
共
E
e
e
⫺E
g
g
兲
␦
e
e
兴
⫽0,
兵
e
其
⫽
兵
e
其
, ᭙
e
, 共9兲
where r
e
e
is the ratio,
r
e
e
⫽S
g
e
/S
g
e
共10兲
共the index
g
is understood in r
e
e
). There are M simulta-
neous equations in Eq. 共9兲 but only M⫺ 1 unknown ratios;
hence one of these equations is redundant. Any one can be
omitted 共assuming the remaining set is nonsingular兲 and our
choice is to remove the equation corresponding to
e
⫽
e
.
In order to obtain S
g
e
from the ratios r
e
e
we use the nor-
malization condition,
兺
e
M
S
g
e
2
⫽
兺
e
M
具
g
g
兩
e
e
典具
e
e
兩
g
g
典
⫽1, 共11兲
which leads to
S
g
e
⫽1
冒
冑
兺
e
M
共
r
e
e
兲
2
. 共12兲
The remaining S
g
e
are obtained from Eq. 共10兲 as S
g
e
⫽r
e
e
S
g
e
(
e
⫽
e
). Finally, the Franck–Condon factors
are given by the square of the corresponding Franck–
Condon integrals (F
g
e
⫽S
g
e
2
).
B. Duschinsky rotations
In general the equilibrium geometry and the potential-
energy surface 共PES兲 of the electronic excited and ground
states are not the same. Therefore the respective normal co-
ordinates Q
e
and Q
g
are also different. The relationship be-
tween the two sets of normal coordinates can be obtained
from the corresponding relationship between their mass-
weighted Cartesian displacement coordinates and the formu-
las that connect the normal and Cartesian coordinates. For
the mass-weighted Cartesian displacement coordinates we
have
X
g
⫽X
e
⫹R, 共13兲
where X
g
(X
e
) represents the coordinates of the electronic
ground 共excited兲 state and R is the vector 共in mass-weighted
Cartesians兲 obtained by subtracting the ground-state equilib-
rium geometry from that of the excited state. The normal
coordinates are related to the mass-weighted Cartesian coor-
dinates by
Q
g
⫽L
g
†
X
g
and Q
e
⫽L
e
†
X
e
, 共14兲
where L
g
and L
e
are unitary matrices 共see, for example, Ref.
41兲. Six columns of L
g
and L
e
共or five for linear molecules兲
are associated with translations and rotations, while the re-
mainder correspond to the normal vibrations. By combining
Eqs. 共13兲 and 共14兲 we find that
Q
g
⫽JQ
e
⫹K, 共15兲
where J⫽L
g
†
L
e
and K⫽L
g
†
R. The J matrix describes the
Duschinsky rotation between the normal modes of the
ground and excited electronic state, while K is associated
with the change in the normal modes due to the displacement
of the equilibrium geometry between the two electronic
states.
The effect of the Duschinsky rotation and the equilib-
rium geometry displacement on the Franck–Condon factors
occurs in the potential-energy difference V
ˆ
g
⫺V
ˆ
e
in Eq. 共9兲
which, for nonlinear states, is given by
V
ˆ
g
⫺V
ˆ
e
⫽V
Q
g
⫽0
g
⫺V
Q
e
⫽0
e
⫹
1
2
兺
i⫽1
3N⫺6
冉
2
V
g
共
Q
i
g
兲
2
冊
Q
g
⫽0
⫻
冋
K
i
2
⫹2K
i
兺
j⫽1
3N⫺6
J
ij
Q
j
e
⫹
兺
j,k⫽1
3N⫺6
J
ij
J
ik
Q
j
e
Q
k
e
册
⫺
1
2
兺
i⫽1
3N⫺6
冉
2
V
e
共
Q
i
e
兲
2
冊
Q
e
⫽0
共
Q
i
e
兲
2
共16兲
in the harmonic approximation.
C. Mechanical anharmonicity
Mechanical anharmonicity can be included through a
perturbation treatment using the harmonic oscillator Hamil-
tonian as the zeroth-order approximation.
42
An alternative
approach is to introduce the anharmonicity by using curvi-
linear coordinates.
31
Expanding Eq. 共8兲 in orders of perturbation theory, we
find that the first-order equation is
兺
e
S
g
e
共
1
兲
关
具
e
e
兩
V
ˆ
g
⫺V
ˆ
e
兩
e
e
典
⫹
共
E
e
e
⫺E
g
g
兲
␦
e
e
兴
共
0
兲
⫹
兺
e
S
g
e
共
0
兲
关
具
e
e
兩
V
ˆ
g
⫺V
ˆ
e
兩
e
e
典
⫹
共
E
e
e
⫺E
g
g
兲
␦
e
e
兴
共
1
兲
⫽0, 共17兲
where the superscripts 共0兲 and 共1兲 indicate the order of per-
turbation theory. The zeroth-order equation is identical to Eq.
共8兲 except that all quantities have a superscript 共0兲. This in-
finite set of equations is truncated to the same finite set
兵
e
其
⫽
兵
e
其
that is used in the zeroth-order equation. As in
previous work
32
we take the cubic terms in V
g
and V
e
to be
first order. In that event, the first-order corrections to E
e
e
and
E
g
g
vanish. On the other hand, the first-order corrections to
the terms in which the potential-energy difference occurs in
Eq. 共17兲 are given by
815J. Chem. Phys., Vol. 120, No. 2, 8 January 2004 Franck–Condon factors
Downloaded 31 Dec 2003 to 130.206.124.176. Redistribution subject to AIP license or copyright, see http://ojps.aip.org/jcpo/jcpcr.jsp

具
e
e
兩
V
ˆ
g
⫺V
ˆ
e
兩
e
e
典
共
1
兲
⫽
具
e
e
共
1
兲
兩
共
V
ˆ
g
⫺V
ˆ
e
兲
共
0
兲
兩
e
e
共
0
兲
典
⫹
具
e
e
共
0
兲
兩
共
V
ˆ
g
⫺V
ˆ
e
兲
共
1
兲
兩
e
e
共
0
兲
典
⫹
具
e
e
共
0
兲
兩
共
V
ˆ
g
⫺V
ˆ
e
兲
共
0
兲
兩
e
e
共
1
兲
典
, 共18兲
where
兩
e
e
共
1
兲
典
⫽⫺
兺
e
⫽
e
M
具
e
e
共
0
兲
兩
V
ˆ
e
共
1
兲
兩
e
e
共
0
兲
典
兩
e
e
共
0
兲
典
E
e
e
共
0
兲
⫺E
e
e
共
0
兲
共19兲
and
共
V
ˆ
g
⫺V
ˆ
e
兲
共
1
兲
⫽
1
6
兺
i,j,k⫽ 1
3N⫺6
冉
3
V
g
Q
i
g
Q
j
g
Q
k
g
冊
Q
g
⫽0
⫻
冋
K
i
K
j
K
k
⫹3K
i
K
j
兺
l⫽1
3N⫺6
J
kl
Q
l
e
⫹3K
i
兺
l,m⫽1
3N⫺6
J
jl
J
km
Q
l
e
Q
m
e
⫹
兺
l,m,n⫽1
3N⫺6
J
il
J
jm
J
kn
Q
l
e
Q
m
e
Q
n
e
册
⫺
1
6
兺
i,j,k⫽ 1
3N⫺6
冉
3
V
e
Q
i
e
Q
j
e
Q
k
e
冊
Q
e
⫽0
Q
i
e
Q
j
e
Q
k
e
.
共20兲
The column vector S
v
g
(1)
with components S
g
e
(1)
, can be
written as
S
v
g
共
1
兲
⫽S
v
g
⬘
共
1
兲
⫹S
v
g
⬙
共
1
兲
⫽S
v
g
⬘
共
1
兲
⫹ fS
v
g
共
0
兲
, 共21兲
where S
v
g
⬘
(1)
is the component of S
v
g
(1)
orthogonal to S
v
g
(0)
and
S
v
g
⬙
(1)
is the component of S
v
g
(1)
parallel to S
v
g
(0)
. The first term
on the left-hand side of Eq. 共17兲 vanishes if we substitute
S
v
g
(0)
for the first-order eigenvector S
v
g
(1)
关cf. Eq. 共8兲兴. There-
fore S
v
g
(1)
is a solution of Eq. 共17兲 for any arbitrary f.We
choose f equal to zero so that S
v
g
(1)
is orthogonal to S
v
g
(0)
and
thereby satisfies the first-order normalization condition
2
兺
e
S
g
e
共
1
兲
S
g
e
共
0
兲
⫽2S
v
g
共
1
兲
†
S
v
g
共
0
兲
⫽0. 共22兲
One easy procedure to solve the set of simultaneous equa-
tions 共17兲 is to transform to a basis consisting of the vector
S
v
g
(0)
and an arbitrary set of M⫺1 vectors perpendicular to
S
v
g
(0)
. Then we only need to solve the reduced set of M⫺1
inhomogeneous equations in the subspace orthogonal to
S
v
g
(0)
. Once the solution for S
g
e
(1)
has been determined, the
first-order corrections to the FCF’s are found as
F
g
e
共
1
兲
⫽2S
g
e
共
0
兲
S
g
e
共
1
兲
. 共23兲
A similar procedure may be followed for the second-
order correction which is obtained by solving
兺
e
M
S
g
e
⬘
共
2
兲
关
具
e
e
兩
V
ˆ
g
⫺V
ˆ
e
兩
e
e
典
⫹
共
E
e
e
⫺E
g
g
兲
␦
e
e
兴
共
0
兲
⫹
兺
e
M
S
g
e
⬙
共
2
兲
关
具
e
e
兩
V
ˆ
g
⫺V
ˆ
e
兩
e
e
典
⫹
共
E
e
e
⫺E
g
g
兲
␦
e
e
兴
共
0
兲
⫹
兺
e
M
S
g
e
共
1
兲
关
具
e
e
兩
V
ˆ
g
⫺V
ˆ
e
兩
e
e
典
⫹
共
E
g
e
⫺E
g
g
兲
␦
e
e
兴
共
1
兲
⫹
兺
e
M
S
g
e
共
0
兲
关
具
e
e
兩
V
ˆ
g
⫺V
ˆ
e
兩
e
e
典
⫹
共
E
e
e
⫺E
g
g
兲
␦
e
e
兴
共
2
兲
⫽0, 共24兲
where we have written S
v
g
⬘
(2)
for the component of S
v
g
(2)
or-
thogonal to S
v
g
(0)
and S
v
g
⬙
(2)
for the component of S
v
g
⬘
(2)
parallel
to S
v
g
(0)
. Again the parallel component is given by S
v
g
⬙
(2)
⫽ fS
v
g
(0)
where the multiplicative constant f is chosen to sat-
isfy the normalization condition which, in second-order, is
0⫽ 2S
v
g
共
2
兲
†
S
v
g
共
0
兲
⫹S
v
g
共
1
兲
†
S
v
g
共
1
兲
⫽2S
v
g
⬙
共
2
兲
†
S
v
g
共
0
兲
⫹S
v
g
共
1
兲
†
S
v
g
共
1
兲
⫽2 f⫹ S
v
g
共
1
兲
†
S
v
g
共
1
兲
共25兲
or
f⫽⫺0.5S
v
g
共
1
兲
†
S
v
g
共
1
兲
. 共26兲
In this case V
e(2)
and V
g(2)
contain the quartic terms in the
expansion of the vibrational potential in terms of normal
coordinates:
共
V
ˆ
g
⫺V
ˆ
e
兲
共
2
兲
⫽
1
24
兺
i,j,k,l⫽1
3N⫺6
冉
4
V
g
Q
i
g
Q
j
g
Q
k
g
Q
l
g
冊
Q
g
⫽0
冋
K
i
K
j
K
k
K
l
⫹4K
i
K
j
K
k
兺
m⫽1
3N⫺6
J
lm
Q
m
e
⫹6K
i
K
j
⫻
兺
m,n⫽1
3N⫺6
J
km
J
ln
Q
m
e
Q
n
e
⫹4K
i
兺
m,n,p⫽1
3N⫺6
J
jm
J
kn
J
lp
Q
m
e
Q
n
e
Q
p
e
⫹
兺
m,n,p,q⫽1
3N⫺6
J
im
J
jn
J
kp
J
lq
Q
m
e
Q
n
e
Q
p
e
Q
q
e
册
⫺
1
24
兺
i,j,k,l⫽1
3N⫺6
冉
4
V
e
Q
i
e
Q
j
e
Q
k
e
Q
l
e
冊
Q
e
⫽0
Q
i
e
Q
j
e
Q
k
e
Q
l
e
. 共27兲
816 J. Chem. Phys., Vol. 120, No. 2, 8 January 2004 Luis, Bishop, and Kirtman
Downloaded 31 Dec 2003 to 130.206.124.176. Redistribution subject to AIP license or copyright, see http://ojps.aip.org/jcpo/jcpcr.jsp

Then S
v
g
(2)
is obtained by solving Eq. 共24兲 for S
v
g
⬘
(2)
in a basis
orthogonal to S
v
g
(0)
and adding S
v
g
⬙
(2)
⫽ fS
v
g
(0)
with the value of
f determined by Eq. 共26兲. Finally, the second-order correction
to the Franck–Condon factors is given by
F
g
g
共
2
兲
⫽2S
g
e
共
0
兲
S
g
e
共
2
兲
⫹S
g
e
共
1
兲
S
g
e
共
1
兲
. 共28兲
D. Truncation of the vibrational basis set
It is critical to perform the truncation of the vibrational
basis set in a way that is efficient and does not create signifi-
cant error. Our procedure involves an iterative buildup by
increasing the range of vibrational quantum numbers while,
simultaneously, removing unimportant states.
We begin by identifying an initial guess for the vibra-
tional state associated with the vertical FC transition to the
excited electronic state based on energy and geometry con-
siderations. This gives a starting set of vibrational quantum
numbers for all modes. Next, an initial basis set is formed
which contains all vibrational wave functions wherein the
quantum number for each mode differs by less than two units
from the corresponding quantum number in the vertical FC
state. Equation 共9兲 is solved in this basis to yield an initial set
of FC overlaps S
v
g. Augmentation of the basis set is, then,
carried out iteratively. In each iterative cycle we, simulta-
neously, increase by one unit the maximum quantum number
of all modes where the previous two augmentations pro-
duced one or more states that have a non-negligible FC over-
lap 共i.e., an overlap larger than 10
⫺6
). An exactly analogous
procedure is applied at the same time to the minimum quan-
tum number except, of course, that the minimum cannot be
reduced below zero. The next step in the cycle is a screening
of the states created in this manner which is based on the
difference between the quantum number in each mode and
the corresponding quantum number for the FC state. If the
sum over modes of the absolute value of these differences for
any given state is larger than a threshold value, then that state
is removed. The threshold is taken to be the largest differ-
ence between the maximum and minimum quantum numbers
in any one mode considering all states. Mok et al. employed
a similar screening criterion to reduce their basis sets.
25
Us-
ing this reduced basis Eq. 共9兲 is solved and a new set of FC
overlap integrals S
v
g is obtained.
Although the algorithm described above limits the
growth of the basis set, the latter still increases in size more
rapidly than desired. It turns out, however, that most of the
FC overlaps obtained from Eq. 共9兲 are quite small. Therefore
the cycle is completed by setting all S
v
g smaller than a pre-
set threshold (10
⫺6
) equal to zero, and the corresponding
states are marked for exclusion in subsequent cycles. They
are retained, however, for the purpose of augmentation. This
simple procedure drastically reduces the growth of the basis
set thereby leading to a major improvement in efficiency.
The overall process is converged when a complete cycle
leads to no augmentation of the basis set.
We tested our algorithm in several different ways for
ClO
2
. Thus the calculations were repeated separately with:
共i兲 the FC overlap threshold for expanding the range of quan-
tum numbers systematically decreased from 10
⫺4
to 10
⫺9
,
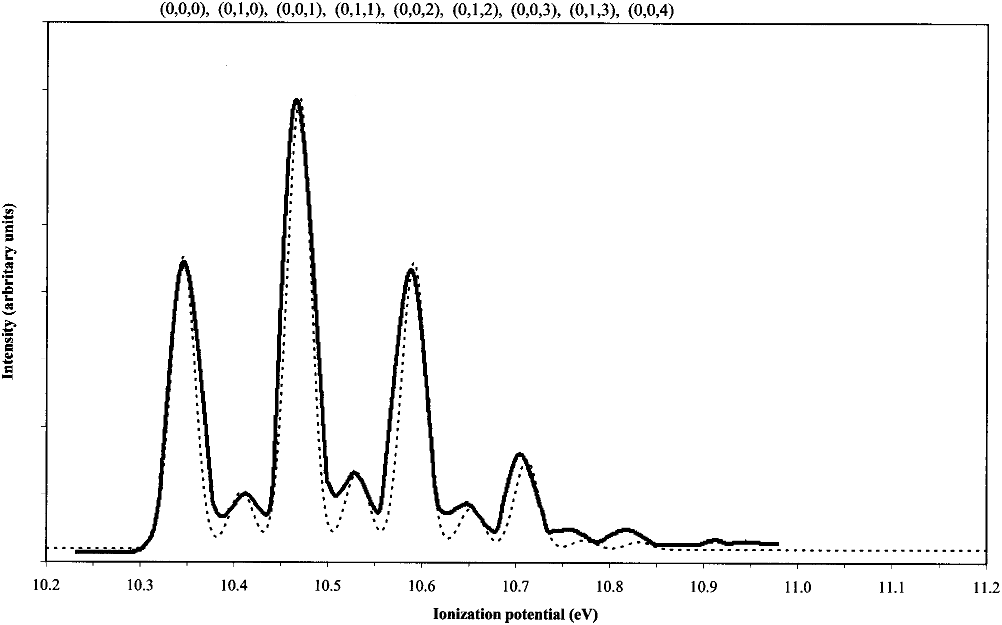
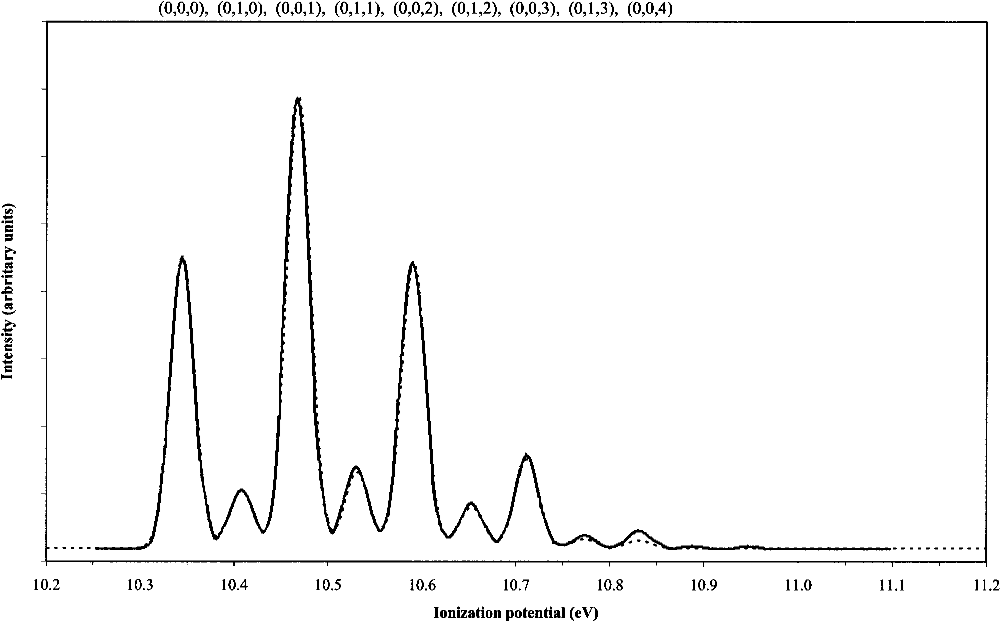
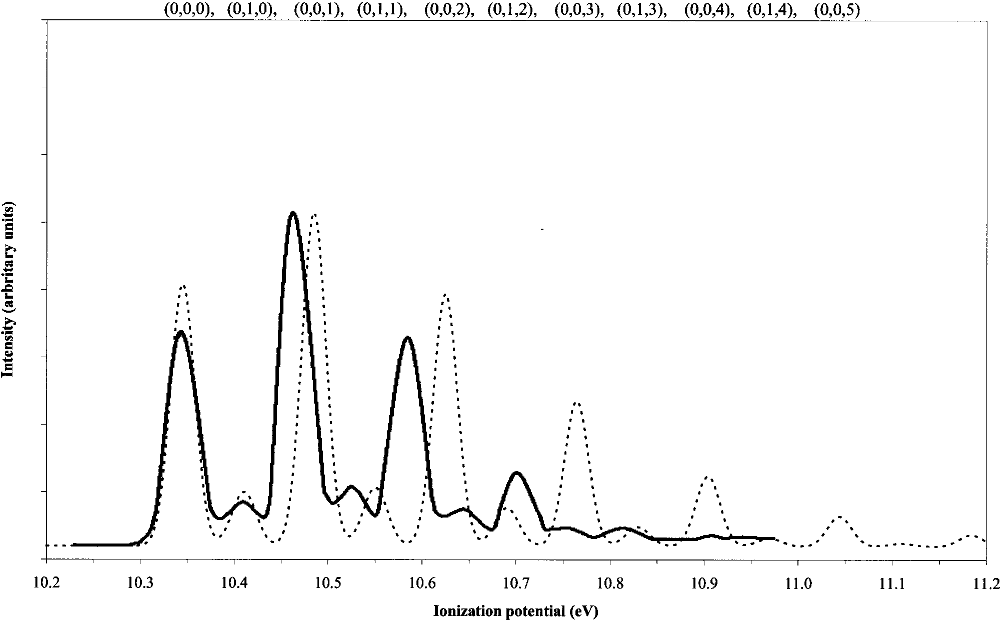
FIG. 1. Simulated first band of the ClO
2
He I PE spectrum using harmonic FCF’s obtained from the QCISD PES. The dashed and solid lines represent our
work and that of Mok et al. 共Ref. 25兲, respectively. The geometry of ClO
2
is the experimental one 共Refs. 51 and 52兲 and the geometrical parameters of the
cation are R
Cl–O
⫽1.410 Å and
O–Cl–O
⫽121.8°.
817J. Chem. Phys., Vol. 120, No. 2, 8 January 2004 Franck–Condon factors
Downloaded 31 Dec 2003 to 130.206.124.176. Redistribution subject to AIP license or copyright, see http://ojps.aip.org/jcpo/jcpcr.jsp