A fractional step method to compute a class of compressible gas–liquid flows

TL;DR: In this article, the authors present some algorithms dedicated to the computation of numerical approximations of a class of two-fluid two-phase flow models and give the main properties of these models.

About: This article is published in Computers & Fluids.The article was published on 2012-02-15 and is currently open access. It has received 48 citations till now. The article focuses on the topics: Relaxation (approximation) & Uniqueness.

Summary

1 Introduction

• Two distinct types of models are used in order to compute liquid-gas or watervapour two-phase flows in industrial codes: the homogeneous approach and the two-fluid approach.
• The two-fluid approach is assumed to be more general, and it is also expected to predict more accurately flows for which the phasic desequilibrium plays a crucial role (see [9, 25, 26]).
• One must be aware that at least two difficulties are hidden in these sets of PDE.
• The second section gives emphasis on the approximation of velocity-pressure-temperature relaxation effects.

2.1 The two-fluid model

• Throughout the paper, indexes l, g refer to the liquid and gas phases; the statistical void fractions of gas and liquid are noted classically αg and αl, which should agree with: αl + αg = 1.
• The so-called conservative variable W will be defined as: W = (αl, αlρl, αlρlUl, αlEl, αgρg, αgρgUg, αgEg) Moreover, PI(W ) and VI(W ) respectively denote in this paper the interfacial pressure and velocity, and will precised afterwards.
• The term S1,l will also be introduced later on.
• External sources might be included but are not considered herein.
• Standard viscous contributions may be included, which of course comply with the entropy inequality that will be detailed in the next subsection.

2.2 Closure laws for interfacial transfer terms

• The same holds when tackling three-phase flows, as emphasized in [18].
• Now, the second requirement (H1) implies that the field associated with λ = VI should be linearly degenerate.
• As shown in [8, 11], few expressions guarantee this behaviour.

2.4 Main properties of the two-fluid model

• The authors may now recall in brief the main properties of system (2) using the previous closure laws.
• Apart from the field associated with the eigenvalue λ =.
• Otherwise the computation of shock solutions would be meaningless, since multiple shock solutions may be obtained using various -stable- solvers (see for examples [17]) .
• Obviously, an alternative formulation of jump conditions in genuinely non linear fields that is probably more convenient may be: σ = [ρφUφ]RL/[ρφ].

3.2 Computing the evolution step

• Many solvers have been proposed in the literature for such a purpose.
• Approximate solutions in the evolution step may also be obtained using either the non-conservative form of Rusanov scheme, or the non-conservative form of the approximate Godunov scheme VFRoe-ncv [6]; the authors refer to [11, 10] for such a description.
• Obviously, the ultimate scheme has not been proposed yet.
• The proof is classical but is briefly recalled.
• The authors detail afterwards the relaxation step, with special focus on the pressure relaxation step which is rather tricky.

3.3 Computing the velocity relaxation step

• It may be easily checked that internal energies remain positive through this step.
• The proof is obvious considering formula (16) and is left to the reader.

3.4 Computing the temperature relaxation step

• The proof provides a practical way to compute solutions of system (18), that is actually used in the code.
• The authors emphasize that other -simpler- algorithms may be exhibited ; however, practical computations seem to show that the non-linear temperature relaxation scheme described here provides better results (see [24] and section IV).
• The authors turn now to the most difficult part which corresponds to the pressure relaxation step.

3.5 Computing the pressure relaxation step

• The first one is a semi-implicit scheme, that is such that the existence and uniqueness of the discrete solution is ensured, whatever the equations of state would be.
• The authors focus here on the second one which is totally implicit with respect to the unknown (Pl, Pg, αl).
• The main lines of the proof are given below, also known as Proof.
• The implicit scheme (20) is exactly the same as the one introduced for dense granular gas-particle flows in [10], also known as Remark 2.

4 Numerical results

• In the first subsection, the authors focus on the computation of the evolution step involving all convective terms.
• The following unities are used : m for distances, kg/m3 for densities, m/s for velocities, Pa for pressures, K for temperatures, s for times and J/s/m2 for heating fluxes.

4.1 Verification of the evolution step

• The authors use for this test case perfect gas EOS within each phase, setting γg = 1.4 and γl = 1.1.
• The second test case is another Riemann problem taken from [13], where initial conditions are given in table 2.
• This Riemann problem also contains a contact wave associated with Ug, and a right-going gas shock wave.

4.2.1 Velocity relaxation substep

• Two different series of verification test cases have been considered in [24] for the velocity relaxation step.
• The first one refers to a constant time scale τ3.
• In that case, the scheme (16) is perfect, since it computes the exact value at time tn+1.
• In that case, analytic solutions allow computing the true error occuring in the velocity relaxation step.
• Several examples can be found in [24], which confirm that a first-order rate of convergence is achieved.

4.2.2 Temperature relaxation substep

• The authors present below some tests corresponding to constant time scales τ4, when computing approximate solutions of (17) with the scheme (18).
• Φ, unlike the non-linear scheme (18); actually, round-off errors are found for the linear scheme in that case.

4.2.3 Pressure relaxation substep

• Eventually, the authors provide an example of measured convergence rates in the pressure relaxation step.
• This one is crucial, and should be handled with great care.
• Otherwise, both the present model (where the relaxation time scale τ2 is non-zero) and standard two-fluid models (corresponding to τ2 = 0) may be confused, if inadequate “rough” schemes are used to provide approximate solutions of (19).
• The initial conditions of the test case are given in table 5. Figure 6 and Figure 7 show the behaviour of the scheme (20) and the comparison with another half-implicit scheme introduced in [22] and recalled in [24], focusing on void fractions and pressures within each phase at time t = 10−5.
• This enables to retrieve the fact that the initial-value problem associated with τ2 = 0 is ill-posed: spurious oscillations arise when the mesh size is sufficiently small, and this is particularly spectacular for void fraction profiles, since the algorithm guarantees bounded variations owing to properties 4 and 5 (see [21] and [17] also for a similar study).

4.3 Two-dimensional numerical results

• The authors consider now the two-dimensional unsteady computation of a heated wall in an almost square domain, where the wall contains a small cavity in the middle of the lower part .
• On the contrary the two cells at the exit corners of the cavity do not receive any heat flux.
• It also seems worth mentionning that almost similar results have been obtained while changing the pressure relaxation time step within the range τ2 ∈ [10−9, 10−6], keeping other relaxation time steps unchanged and using the same mesh.
• Nonetheless, one must be aware that the 3D counterpart of the present 2D mesh would contain more than 150 millions of cells, which is of course far beyond what one can afford in an industrial situation.

Figures

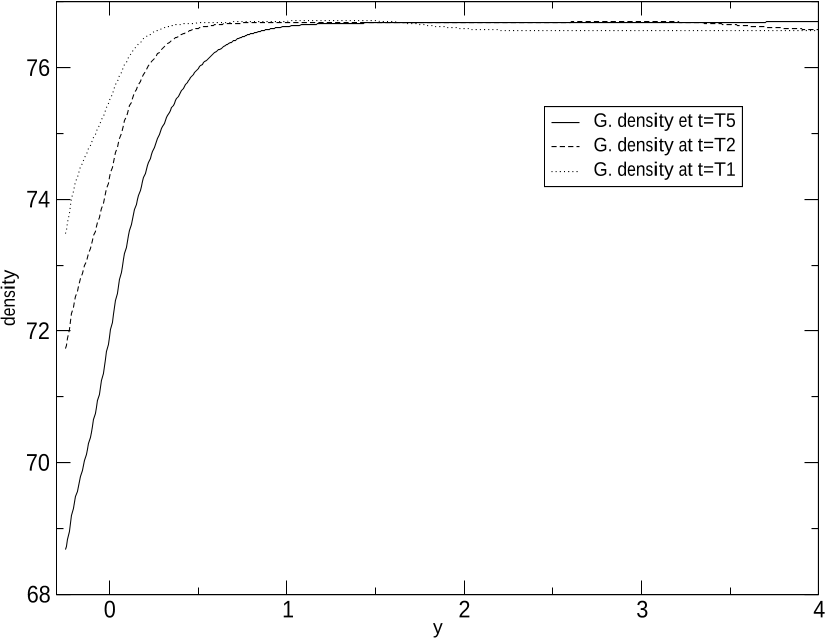
Figure 11: Heated wall: y-profile of the gas density ρg at three distinct times T = T1 (dotted line), T2 (dashed line), T5 (plain line), at: x = 2. The small cavity in the wall boundary corresponds to −0.25 < y < 0.

Table 1: : Initial condition for the first Riemann problem and intermediate states.

Figure 3: Approximate solution of the second Riemann problem obtained with 100000 cells and the exact solution (ex.) at time t = 1.4 10−4. Top left: liquid fraction, top right: pressures, bottom left: densities, bottom right: velocities.

Figure 2: L1 norm of the error for the first Riemann problem. Plain lines: gas, dotted lines: liquid. Liquid mass fraction (crosses), velocities (squares), pressures (triangles), densities (circles). Meshes contain 500000, 250000, 50000, 5000, 500 and 50 regular cells.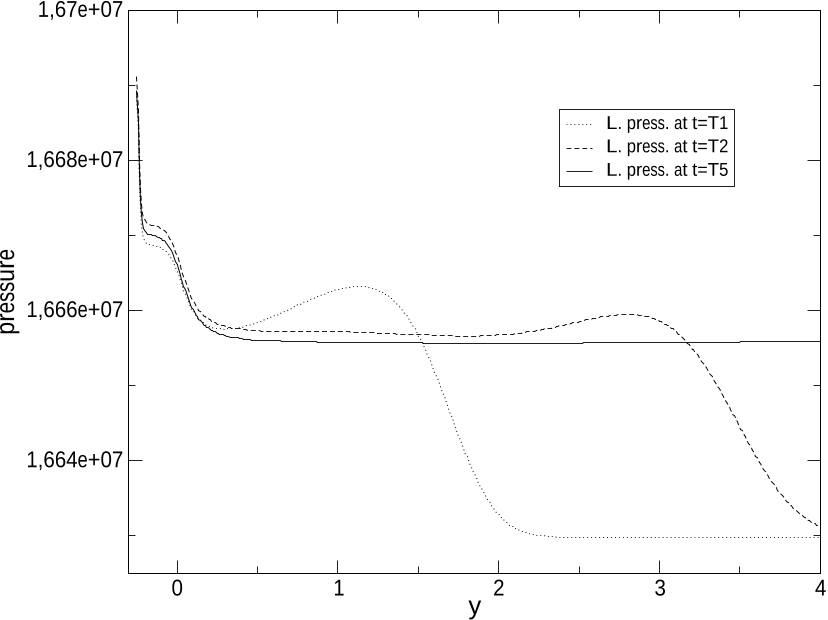

Figure 12: Heated wall: y-profiles of gas and liquid pressures Pg, Pl at three distinct times T = T1 (dotted line), T2 (dashed line), T5 (plain line), at: x = 2. The small cavity in the wall boundary corresponds to −0.25 < y < 0.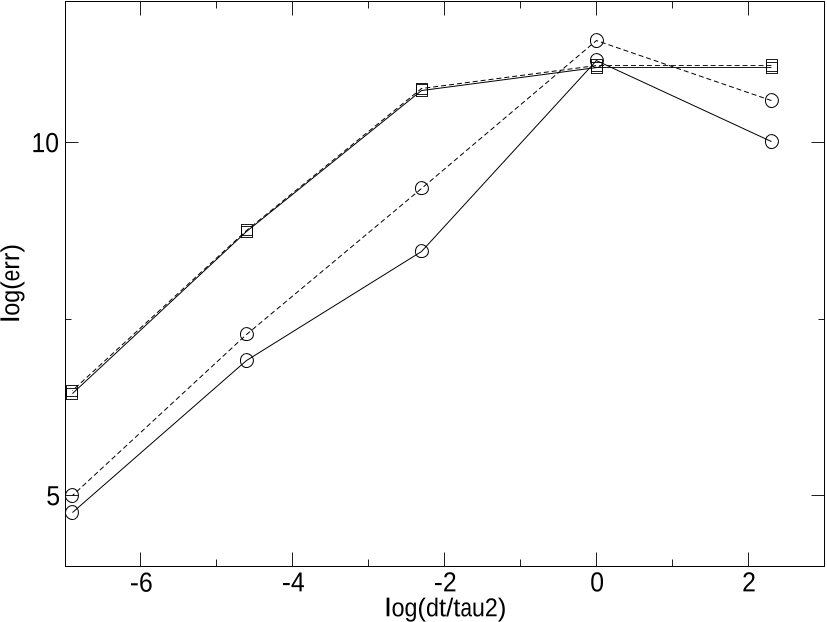

Figure 7: Pressure relaxation substep: measured L1 norm of the error for the liquid pressure (straight line) and the gas pressure (dotted line) at time T = 10−5 as a function of ∆t/τ2 = {10, 1, 10−1, 10−2, 10−3}. Implicit scheme (20) (circles) versus half-implicit scheme (squares).

Figure 6: Pressure relaxation substep: measured L1 norm of the error for the void fraction at time T = 10−5 as a function of ∆t/τ2 = {10, 1, 10−1, 10−2, 10−3}. Implicit scheme (20) (circles) versus half-implicit scheme (squares).

Figure 8: Heated wall: sketch of the computational domain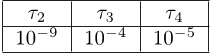

Table 6: : Values of time scales in the 2D experiment.

Figure 1: Approximate solution of the first Riemann problem obtained with 500000 cells and the exact solution (ex.) at time t = 1.4 10−4. Top left: liquid fraction, top right: pressures, bottom left: densities, bottom right: velocities.

Figure 13: Heated wall: y-profiles at x = 2 for the liquid void fraction (top left), pressures (top right), velocities in the y-direction (bottom left) and densities (bottom right) at time T = T1. Liquid phase: plain line, gas phase: dashed line.

Figure 9: Heated wall: contours of the liquid pressure PL in the computational domain at time T = T1.

Table 4: : Initial condition for the temperature relaxation test case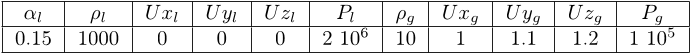

Table 5: : Initial condition for the pressure relaxation test case

Figure 5: Temperature relaxation substep: error at time T = 10−5 as a function of ∆t/τ4 = {1, 10−1, 10−2, 10−4, 10−6}. Liquid temperature (straight line), gas temperature (dotted line). Linear scheme (circles) versus non-linear scheme (squares).

Figure 14: Approximate solution of the first Riemann problem described in [35] (table 1, p. 499) for 50, 500 and 5000 cells.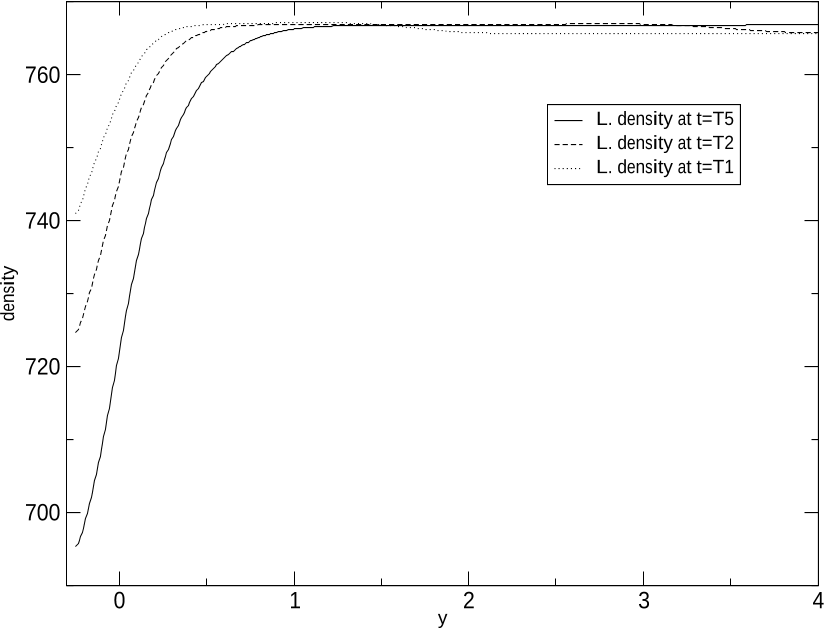

Figure 10: Heated wall: y-profile of the liquid density ρl at three distinct times T = T1 (dotted line), T2 (dashed line), T5 (plain line), at: x = 2. The small cavity in the wall boundary corresponds to −0.25 < y < 0.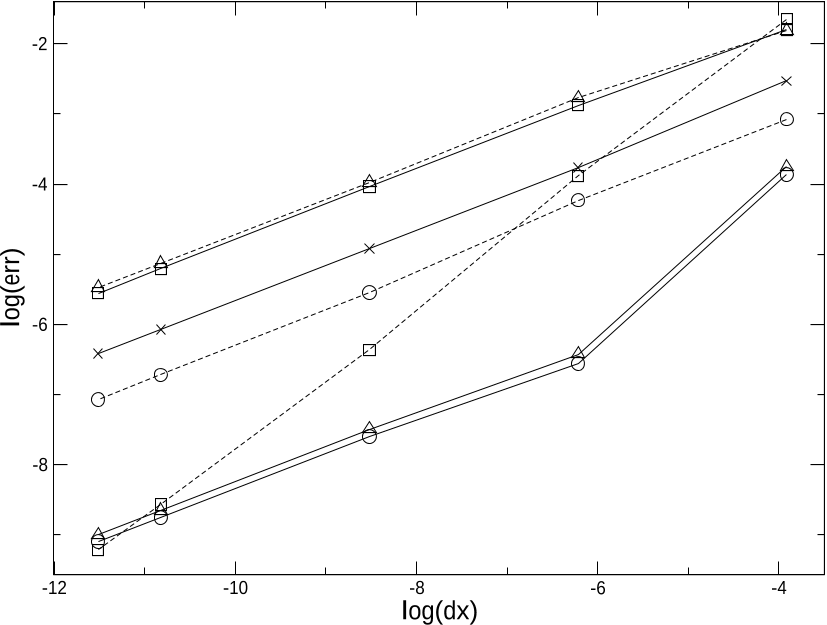

Figure 4: L1 norm of the error for the second Riemann problem. Plain lines: liquid, dotted lines: gas. Liquid mass fraction (crosses), velocities (squares), pressures (triangles), densities (circles). Meshes contain 100000, 50000, 5000, 500 and 50 regular cells.

Table 2: : Initial condition for the second Riemann problem and intermediate states.

Table 3: : Initial condition for the first Riemann problem described in [35] (table 1, p. 499).