A general condition for the existence of unconnected equilibria for symmetric arches

TL;DR: In this paper, a general condition for the existence of unconnected equilibria for symmetric shallow arches is derived for the first time, which can directly determine whether or not a shallow arch with specific initial configuration and external load has remote unconnected equilibrium states.

Abstract: This paper presents a semi-analytical study of unconnected equilibrium states for symmetric curved beams. Using the Fourier series approximation, a general condition for the existence of unconnected equilibria for symmetric shallow arches is derived for the first time. With this derived condition, we can directly determine whether or not a shallow arch with specific initial configuration and external load has remote unconnected equilibria. These unconnected equilibria cannot be obtained in experiments or nonlinear finite element simulations without performing a proper perturbation first. The derived general condition is then applied to curved beams with different initial shapes and external loads. It is found that initially symmetric parabolic arches under a uniformly distributed vertical force can have multiple groups of unconnected equilibria, depending on the initial rise of the structure. However, small symmetric geometric deviations are required for parabolic arches under a central point load, and half-sine arches under a central point load or a uniformly distributed load to have unconnected equilibria. The validity of the analytical derivations of the nonlinear equilibrium solutions and the general condition for the existence of unconnected equilibria are verified by nonlinear finite element methods.

Summary

1. Introduction

• Curved beams have been studied extensively due to their rich nonlinear structural behavior and broad applications in aerospace, civil and mechanical engineering.
• Therefore, only determining snap-through buckling loads is not sufficient and it is also necessary to gain insights into the post-snap responses.
• In the current paper, the authors find that initially symmetric arches may also have unconnected “hidden” equilibria, which is not as initially expected.

2.2. Existence of unconnected equilibria

• Here the superscript ′ denotes the partial derivative with respect to p. A(p), B(p) and C(p) are defined in Eqs. (7).
• Therefore, a general condition that unconnected equilibria starts occurring for symmetric shallow arches can be obtained by solving Eq. (12).

3.1.1. Perfect parabolic arches

• In Fig. 2, solid and dashed lines represent the primary and bifurcated equilibria obtained from the analytical formula respectively.
• In order to obtain remote unconnected equilibria in FEA, the structure is first perturbed to a remote unconnected equilibrium configuration using the information from the analytical solutions.
• When the rise of the arch h = 6.95 is slightly larger than the first critical rise h = 6.91, one group of unconnected equilibria appears, and on this path two critical points (zero tangent, singular stiffness) are present (gray curves in Fig. 2b), separating equilibria with different number of negative eigenvalues.
• For these higher dimension responses, the higher modes corresponding to the unstable equilibria of the system become quite relevant.

3.1.2. Half-sine arches with symmetric geometric deviations

• The derived formulas are applied to half-sine arches with symmetric geometric deviations and under a uniformly distributed load.
• Fig. 7a and 7b show the boundaries separating the cases that have and do not have unconnected equilibria for half-sine arches with symmetric geometric deviations in e3h sin(3ξ) and e5h sin(5ξ) respectively.
• The growing rate of the geometric deviations coefficients tends to become smaller as the rise h increases and the splitting boundaries eventually flatten out.
• When the deviation coefficients are slightly above the splitting boundaries (e3 = 0.0345, cross marker in Fig. 7a, or e5 = 0.0048, cross marker in Fig. 7b), remote unconnected equilibrium states appear for these arches (Fig. 8b and 9b respectively).
• The influence of symmetric geometric deviations on the appearance of unconnected equilibria is however similar to that of asymmetric geometric imperfections [42].

3.2. Concentrated load at the midspan

• From Eq. (7) and (12), the authors can tell that both initial shapes and external loading types can influence the appearance of unconnected equilibria.
• The authors focus on shallow arches subjected to another type of external load, vertical concentrated load applied at the midspan.

3.2.1. Parabolic arches with symmetric geometric deviations

• Unlike arches subjected to uniformly distributed load, perfect parabolic arches under a point load at the midspan do not have unconnected equilibria.
• Small symmetric geometric deviations can lead to the appearance of unconnected equilibrium states.
• Other initial mode coefficients can be found from Eq. (16).
• Fig. 11a and 11b illustrate the splitting boundaries for parabolic arches with symmetric geometric deviations in e3h sin(3ξ) and e5h sin(5ξ) respectively when they are subjected to a central point load.

3.2.2. Half-sine arches with symmetric geometric deviations

• Similar to perfect half-sine arches under uniformly distributed load, the perfect half-sine arches subjected to a point load at the midspan also do not have unconnected equilibria.
• Similar to the previous section, geometric deviations in e3h sin(3ξ) and e5h sin 5ξ are considered, where h is the non-dimensional initial rise of a perfect half-sine arch.
• Fig. 15 and 16 show the equilibria of several representative half-sine arches with geometric deviations that are within and beyond the splitting boundaries.
• Fig. 15a and 16a illustrate the equilibria of arches corresponding to the circle markers in Fig. 14a and 14b, while Fig. 15b and 16b describe the equilibria of arches corresponding to the cross markers in Fig. 14a and 14b.
• As expected, no unconnected equilibria exist in Fig. 15a and 16a and unconnected equilibria appear in Fig. 15b and 16b.

4. Conclusions

• A general condition for the existence of unconnected equilibria for initially symmetric arches is derived by utilizing the Fourier series.
• Under displacement or arc-length control, these unconnected equilibrium states can be obtained in experiments or nonlinear finite element simulations if the system is perturbed to one of the remote unconnected equilibrium configuration under the guidance of analytical solutions.
• The existence of unconnected equilibria is sensitive to the initial shapes and external load types that shallow arches have.
• For perfect parabolic arches under a point load and perfect half-sin arches under a point load or a uniformly distributed load, when certain symmetric geometric deviations for instance e3h sin(3ξ) or e5h sin(5ξ) are added to the structures, unconnected equilibrium states can appear.
• The absolute value of the geometric deviation coefficient e3 or e5 on the splitting boundaries tends to grow and eventually stop varying when the rise of the perfect shaped arch increases.

Figures

Figure 4: The load-displacement relationship corresponding to the equilibrium states shown in Fig. 2f.

Figure 8: The equilibria of half-sine arches with deviations in e3h sin(3ξ).

Figure 3: Eight deformed configurations of the the equilibrium states Ia - IVb in Fig. 2f.

Figure 7: The separating boundaries of half-sine arches under uniformly distribured load with geometric derivation in e3h sin(3ξ) and e5h sin(5ξ) respectively.

Figure 11: The splitting boundaries for parabolic arches with geometric deviations e3h sin(3ξ) and e5h sin(5ξ) under central point load.

Figure 12: The equilibria of parabolic arches with geometric deviations in e3h sin(3ξ) and e5h sin(5ξ).

Figure 6: The equilibria obtained with different number of modes.

Figure 1: A shallow arch under a transverse load.

Figure 14: The splitting boundaries for half-sine arches with geometric deviations e3h sin(3ξ) and e5h sin(5ξ) under central point load.

Figure 13: The equilibria of parabolic arches with deviations in e5h sin(5ξ)

Figure 5: The equilibria of parabolic arches with h = 7.0, 8.0 and 9.0.

Figure 2: The equilibria of parabolic arches with six different rises.

Figure 16: The equilibria of half-sine arches with deviations in e5h sin(5ξ) and under central point load.

Figure 15: The equilibria of half-sine arches with deviations in e3h sin(3ξ) and e5h sin(5ξ).

Figure 10: Equilibrium states of half-sine arches with different geometric deviations in e3h sin(3ξ), where h = 8, e3 = 0.027, 0.044 and 0.058 respectively.

Figure 9: The equilibria of two half-sine arches with deviations in e5h sin(5ξ).

Full text

A general condition for the existence of unconnected
equilibria for symmetric arches
Yang Zhou, Ilinca Stanciulescu
∗
Rice University, Department of Civil and Environmental Engineering, Houston, TX, 77005, U.S.A
Abstract
This paper presents a semi-analytical study of unconnected equilibrium states for symmetric
curved beams. Using the Fourier series approximation, a general condition for the existence
of unconnected equilibria for symmetric shallow arches is derived for the first time. With
this derived condition, we can directly determine whether or not a shallow arch with specific
initial configuration and external load has remote unconnected equilibria. These unconnected
equilibria can not be obtained in experiments or nonlinear finite element simulations without
performing a proper perturbation first. The derived general condition is then applied to
curved beams with different initial shapes and external loads. It is found that initially
symmetric parabolic arches under a uniformly distributed vertical force can have multiple
groups of unconnected equilibria, depending on the initial rise of the structure. However,
small symmetric geometric deviations are required for parabolic arches under a central point
load, and half-sine arches under a central point load or a uniformly distributed load to have
unconnected equilibria. The validity of the analytical derivations of the nonlinear equilibrium
solutions and the general condition for the existence of unconnected equilibria are verified by
nonlinear finite element methods.
Keywords: Unconnected equilibrium states, A general condition, Symmetric curved beams,
Post-buckling responses
1. Introduction
Curved beams have been studied extensively due to their rich nonlinear structural be-
havior and broad applications in aerospace, civil and mechanical engineering. When these
∗
Corresponding author. Tel.: +1713 348 4704; fax: +1713 348 5268.
Email address: ilinca.s@rice.edu (Ilinca Stanciulescu)
Preprint submitted to Elsevier November 18, 2017

arches are loaded transversely, they can jump between coexisting equilibrium configurations,
phenomenon accompanied by rapid curvature reversals. This phenomenon is often referred
to as snap-through buckling and it greatly exacerbates fatigue failure.
Motivated by the goal of avoiding snap-through, a great portion of studies in the early
literature focused on calculating the buckling loads of shallow arches with different geome-
try, boundary and loading conditions. One of the earliest work was included in [1], where
Timoshenko used the first symmetric mode to obtain the solutions for a half-sine arch under
a half-sine load. This study provided some guidance for analyzing snap-through but failed to
consider possible bifurcated branches that involve higher order modes. Following this work,
Fung and Kaplan [2] used few sine terms to obtain the stability boundaries of sine arches
with several different types of transverse loads. Instead of using Fourier series, Schreyer and
Masur [3] directly solved the differential equations analytically and made a special effort to
differentiate symmetric and asymmetric snap-through. These pioneering studies have been
extended by many researchers to examine the influence of elastic boundary constraints on
critical equilibrium states [4–9], to characterize the sensitivity of buckling loads to geometric
and load imperfections [10–17], to derive exact solutions for critical loads without truncat-
ing the Fourier series [18, 19], to incorporate thermal effects in nonlinear buckling analyses
[20–23], and to study the effects of pre-buckling deformations, initial shapes and loading on
the nonlinear stability responses [23–29]. In these investigations, the snap-through buckling
loads were obtained but few efforts were made to characterize the post-buckling responses.
Despite inducing fatigue, snap-through has recently been utilized in developing vibratory
energy harvesters [30, 31], switches [32, 33], sensors [34] and non-volatile memories [35]. In
these applications, the curved beams are designed to undergo snap-through and to work in
the post-buckling region. Therefore, only determining snap-through buckling loads is not
sufficient and it is also necessary to gain insights into the post-snap responses. In fact,
recent studies have continued to reveal new and interesting post-snap responses. Pi and
Bradford [36–38] found that curved beams with unequal boundary conditions may have four
limit points and looping equilibrium states in the post-buckling responses. Moghaddasie and
Stanciluescu [39] identified that more pairs of critical points and more complex post-snap
behaviors can exist for shallow arches in thermal environments. Similar phenomena were also
observed by Hung and Chen [40] for buckled beams on elastic foundations. In addition to the
2

identification of connected complex looping equilibria, Harvey and Virgin [41] demonstrated
that remote equilibria exist for curved beams under an off-center point load in physical
experiments by manually perturbing the structure to a remote configuration. The current
authors Zhou et al. [42] showed that shallow arches with asymmetric geometric imperfections
can have remote unconnected “hidden” equilibria, which are difficult to obtain numerically if
a prior knowledge of these “hidden” equilibria is not available. It was also identified in [42]
that asymmetric geometric imperfections make the bifurcated paths disappear and equilibria
split around these secondary paths.
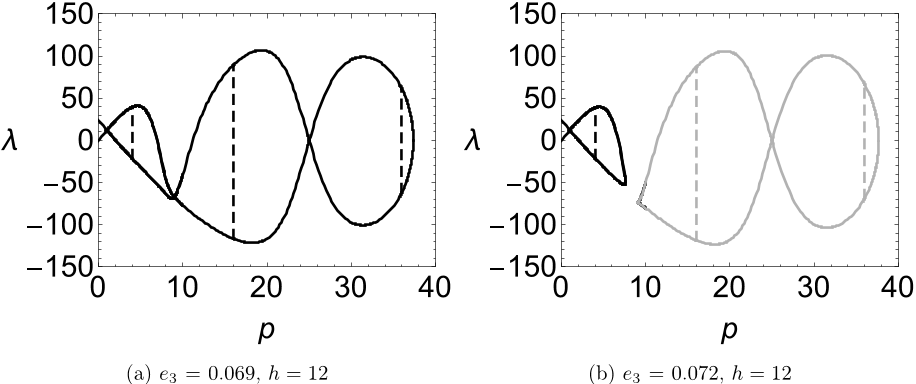
In the current paper, we find that initially symmetric arches may also have unconnected
“hidden” equilibria, which is not as initially expected. Unlike arches with asymmetric geo-
metric imperfections, it is in general difficult to tell when symmetric arches have unconnected
equilibria. Here, a general condition for the existence of unconnected equilibria is derived
for shallow symmetric arches. We apply this general condition on perfect parabolic, half-sine
arches and these arches with small symmetric geometric deviations when they are subjected
to uniformly distributed load and point load in the middle and verify the validity of the gen-
eral condition by comparing the equilibrium states of the structures with parameters below
and above the general condition. It is found that the existence of unconnected equilibria is
very sensitive to the arches’ initial configurations and to the type of external load that they
are subjected to. This work can also help to guide the exploration of the “hidden” equilibria
in numerical and physical experiments.
Remote unconnected equilibria may not affect the static buckling loads of the structures.
However, they can influence the dynamic responses of the structures. Under dynamic pertur-
bations, these structures may jump to remote unconnected configurations. Pi and Bradford
[38] identified that it is crucial to identify all coexisting equilibria of the structures to cor-
rectly determine the dynamic snap-through buckling loads. More recently, Wiebe and Virgin
[43] demonstrated that the presence and location of unstable equilibria can also have a great
impact on the long-term recurrent behavior of a dynamic system. We conjecture that the
identification of remote unconnected equilibria may provide useful information for the design
of devices that take advantage of dynamic snap-through and work under post-snap regions
such as energy harvesters, switches, sensors and non-volatile memories [30–35].
3

2. Governing equations
Using the Fourier series and following [42], the dimensionless algebraic equilibrium equa-
tions of shallow arches under transverse loads (Fig. 1) can be written as
(α
n
− β
n
)n
4
− pn
2
α
n
+ q
n
= 0, n = 1, 2, ..., k, (1)
u(ξ)
u
ξ
π
0
q
(ξ)
Figure 1: A shallow arch under a transverse load.
Here, α
n
represent the mode coefficients of the deformed configurations u(ξ) =
k
P
n=1
α
n
sin(nξ),
β
n
are the mode coefficients of the initial configuration u
0
(ξ) =
k
P
n=1
β
n
sin(nξ), q
n
denote
the mode coefficients of the non-dimensional external load q and can be calculated from
q
n
= (2/π)
R
π
0
q sin (nξ) dξ, k is the number of Fourier Sine terms included, and p is the
dimensionless axial force that can be calculated from
p =
k
X
i=1
i
2
(β
2
i
− α
2
i
)
4
. (2)
A brief description of the procedure involved in deriving Eq. (1) is included in the Appendix
and more details can be found in [42].
2.1. Equilibrium states
Let the external load q(ξ) be expressed as q(ξ) = λq
0
(ξ), where q
0
(ξ) is a reference function
that can be chosen as needed and λ is the loading parameter. It can then be found that the
load coefficients q
n
have a linear relationship with the loading parameter λ for an arbitrary
4

transverse load. The linear relationship is q
n
= γ
n
λ, and γ
n
will be referred as the reference
loading coefficients that can be calculated from
γ
n
=
2
π
Z
π
0
q
0
(ξ) sin(nξ)dξ (3)
Substituting the load coefficients q
n
= γ
n
λ into Eq. (1), the non-dimensional algebraic
equilibrium equation for shallow arches under an arbitrary vertical load can be obtained
(α
n
− β
n
)n
4
− pn
2
α
n
+ λγ
n
= 0, n = 1, 2, ..., k, (4)
The deformation mode coefficients α
n
can then be calculated as
α
n
=
n
4
β
n
− λγ
n
n
2
(n
2
− p)
, n = 1, 2, ..., k (5)
With these deformation mode coefficients α
n
and Eq. (2), we can find that the loading
parameter λ satisfies the following quadratic equation
Aλ
2
+ Bλ + C + 4p = 0 (6)
For a given arch shape and loading case, A, B and C are functions of the axial load p and
are defined as follows:



















A(p) =
k
P
n=1
γ
2
n
n
2
(n
2
− p)
2
B(p) =
k
P
n=1
−2n
2
γ
n
β
n
(n
2
− p)
2
C(p) = 4p +
k
P
n=1

n
6
β
2
n
(n
2
− p)
2
− n
2
β
2
n

(7)
Substituting the mode coefficients α
n
into the deformed configuration u(ξ), the vertical
displacement field ∆u(ξ) can be obtained as
∆u = − (u (ξ) − u
0
(ξ))
=
k
X
n=1
β
n
sin(nξ) −
k
X
n=1
n
2
β
n
(n
2
− p)
sin(nξ) −
k
X
n=1
γ
n
λ
n
2
(n
2
− p)
sin(nξ) (8)
Setting ξ = π/2, the displacement at the midspan can then be derived as
∆u
mid
= D(p)λ + F (p) (9)
5