




Did you find this useful? Give us your feedback













28 citations
...Several authors, like Khoo et al. (2012), Graham, Chakraborti, and Mukherjee (2014), Teoh et al. (2014) and Chakraborty, Human, and Balakrishnan (2018), recommended using median run length (MRL) in place of the ARL, as a robust alternative with various advantages....
[...]
20 citations
14 citations
499 citations
389 citations
148 citations
...However, Sheu and Lin [2], Sheu and Yang [13], Lu [6] and Chakraborty et al....
[...]
...For a detail study on GWMA-X̄ chart for normal distribution, the reader is referred to Sheu and Lin [2]....
[...]
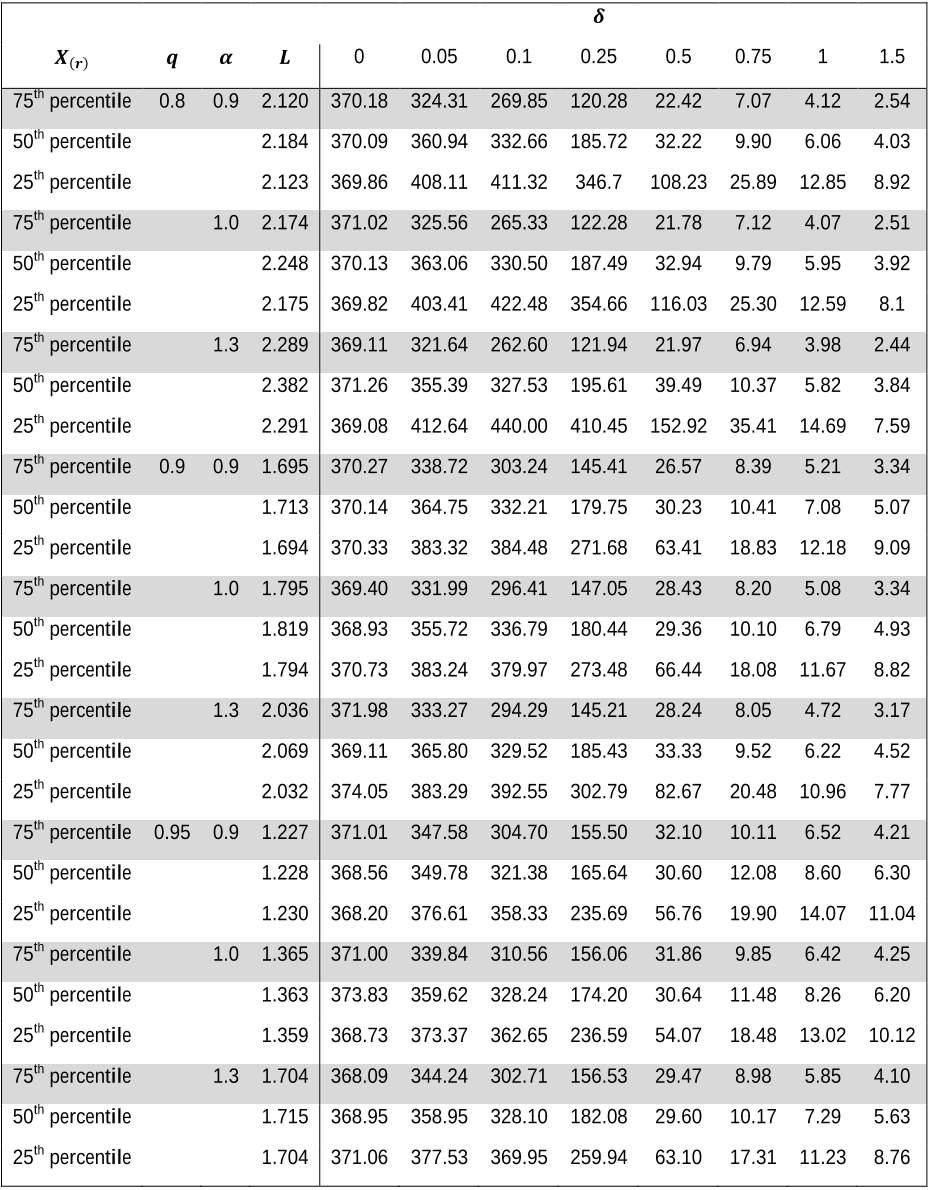
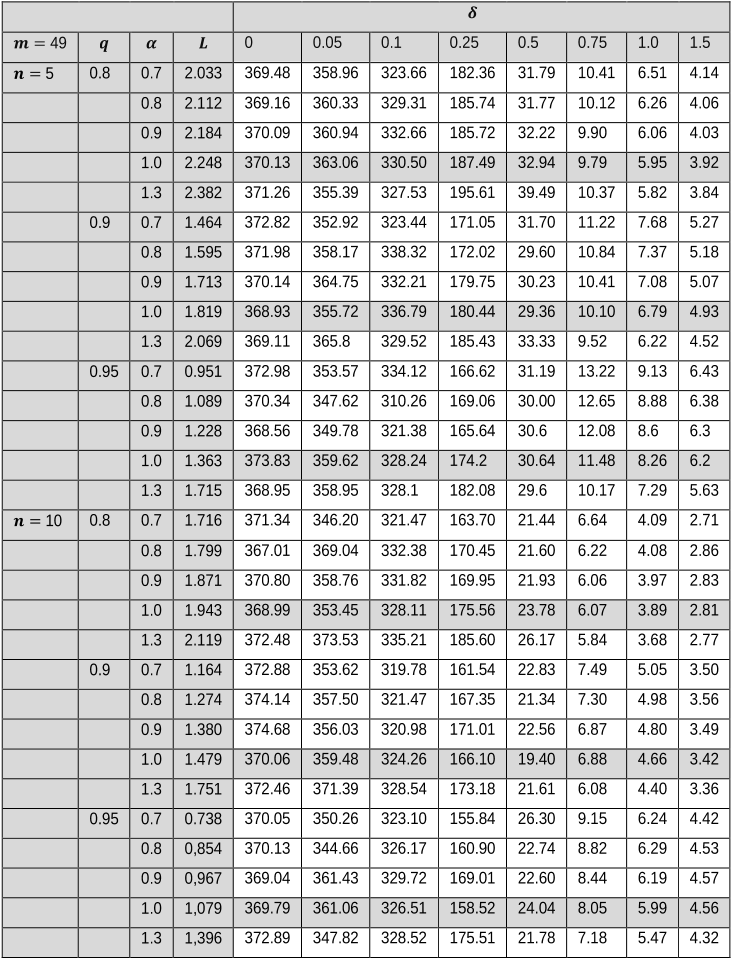
...As in Sheu and Lin [2], the distribution of N is taken to be Pr[N = i] = q(i−1) − qiα , where 0 ≤ q < 1 and α > 0 are the two parameters; this is the discrete two-parameter Weibull distribution (see Nakagawa and Osaki [12])....
[...]
...Generalizing the EWMA charting procedure, Sheu and Lin [2] proposed a Generally Weighted Moving Average (GWMA) control chart for the normal distribution (denoted by GWMA-X̄ chart) that has been shown to be more effective than EWMA, CUSUM and Shewhart-type charts (see Hsu et al....
[...]
...To this end, Sheu and Lin [2] noted that (q,α) combinations in the intervals 0....
[...]
104 citations
101 citations
...[8] studied a class of nonparametric Shewhart-type charts based on precedence statistics, referred to as the Shewhart-type precedence charts....
[...]