Classical and Quantum Gravity
PAPER
A matrix method for quasinormal modes:
Schwarzschild black holes in asymptotically flat
and (anti-) de Sitter spacetimes
To cite this article: Kai Lin and Wei-Liang Qian 2017 Class. Quantum Grav. 34 095004
View the article online for updates and enhancements.
Related content
Black hole quasinormal modes using the
asymptotic iteration method
H T Cho, A S Cornell, Jason Doukas et al.
-
Fermion perturbations in string theory
black holes
Owen Pavel Fernández Piedra and
Jeferson de Oliveira
-
Quasinormal Modes of a Noncommutative-
Geometry-Inspired Schwarzschild Black
Hole
Jun Liang
-
Recent citations
Charged scalar fields around Einstein-
power-Maxwell black holes
Grigoris Panotopoulos
-
The matrix method for black hole
quasinormal modes
Kai Lin and Wei-Liang Qian
-
Quasinormal modes of the BTZ black hole
under scalar perturbations with a non-
minimal coupling: exact spectrum
Grigoris Panotopoulos
-
This content was downloaded from IP address 186.217.236.64 on 04/07/2019 at 20:39

1
Classical and Quantum Gravity
A matrix method for quasinormal
modes: Schwarzschild black holes
inasymptotically at and (anti-)
de Sitter spacetimes
KaiLin
1
,
2
and Wei-LiangQian
2
,
3
1
Universidade Federal de Itajubá, Instituto de Física e Química, Itajubá, MG, Brazil
2
Escola de Engenharia de Lorena, Universidade de São Paulo, Lorena, SP, Brazil
3
Faculdade de Engenharia de Guaratinguetá, Universidade Estadual Paulista,
Guaratinguetá, SP, Brazil
E-mail: lk314159@hotmail.com and wlqian@usp.br
Received 11 January 2017, revised 1 March 2017
Accepted for publication 13 March 2017
Published 31 March 2017
Abstract
In this work, we study the quasinormal modes of Schwarzschild and
Schwarzschild (Anti-) de Sitter black holes by a matrix method. The proposed
method involves discretizing the master eld equationand expressing it in the
form of a homogeneous system of linear algebraic equations. The resulting
homogeneous matrix equationfurnishes a non-standard eigenvalue problem,
which can then be solved numerically to obtain the quasinormal frequencies.
A key feature of the present approach is that the discretization of the wave
function and its derivatives is made to be independent of any specic metric
through coordinate transformation. In many cases, it can be carried out
beforehand, which in turn improves the efciency and facilitates the numerical
implementation. We also analyze the precision and efciency of the present
method as well as compare the results to those obtained by different approaches.
Keywords: quasinormal modes, black hole, Schwarzschild spacetime,
deSitter spacetime
(Some guresmay appear in colour only in the online journal)
1. Introduction
A black hole, long considered to be a physical as well as mathematical curiosity, is derived
in general relativity as a generic prediction. Through gravitational collapse, a stellar-mass
black hole can be formed at the end of the life cycle of a very massive star, when its gravity
K Lin and W-L Qian
A matrix method for quasinormal modes: Schwarzschild black holes in asymptotically flat and (anti-) de Sitter spacetimes
Printed in the UK
095004
CQGRDG
© 2017 IOP Publishing Ltd
34
Class. Quantum Grav.
CQG
1361-6382
10.1088/1361-6382/aa6643
Paper
9
1
13
Classical and Quantum Gravity
IOP
2017
1361-6382/17/095004+13$33.00 © 2017 IOP Publishing Ltd Printed in the UK
Class. Quantum Grav. 34 (2017) 095004 (13pp) https://doi.org/10.1088/1361-6382/aa6643

2
overcomes the neutron degeneracy pressure. A crucial feature of a black hole is the existence
of the event horizon, a boundary in spacetime beyond which events cannot affect an outside
observer. Despite its invisible interior, however, the properties of a black hole can be inferred
through its interaction with other matter. By quantum eld theory in curved spacetime, it is
shown that the event horizons emit Hawking radiation, with the same spectrum of black body
radiation at a temperature determined by its mass, charge and angular momentum [2]. The
latter completes the formulation of black hole thermodynamics [3], which describes the prop-
erties of a black hole in analogy to those of thermodynamics by relating mass to energy, area
to entropy, and surface gravity to temperature. Quasinormal modes (QNMs) arise as the tem-
poral oscillations owing to perturbations in black hole spacetime [5]. Owing to the energy loss
through ux conservation, these modes are not normal. Consequently, when writing the oscil-
lation in an exponential form,
()ω− texpi
, the frequency of the modes is a complex number.
The real part,
ω
R
, represents the actual temporal oscillation; and the imaginary part,
ω
I
, indi-
cates the decay rate. Therefore, these modes are commonly referred to as quasinormal. The
stability of the black hole spacetime guarantees that all small perturbation modes are damped.
Usually, QNMs can be conditionally divided into three stages. The rst stage involves a short
period of the initial outburst of radiation, which is sensitively dependent on the initial condi-
tions. The second stage consists of a long period dominated by the quasinormal oscillations,
where the amplitude of the oscillation decays exponentially in time. This stage is character-
ized by only a few parameters of the black holes, such as their mass, angular momentum, and
charge. The last stage takes place when the QNMs are suppressed by power-law or exponen-
tial late-time tails. The properties of QNMs have been investigated in the context of the AdS/
CFT correspondence [6, 7]. As a matter of fact, practically every stellar object oscillates, and
oscillations produced by very compact stellar objects and their detection are of vital impor-
tance in physics and astrophysics. In 2015, the rst observation of gravitational waves from
a binary black hole merger was reported [4]. The observation provides direct evidence of the
last remaining unproven prediction of general relativity and reconrms its prediction of space-
time distortion on the cosmic scale.
Mathematically, the QNMs are governed by the linearized equationsof general relativity
constraining perturbations around a black hole solution. The resulting master eld equationis
a linear second order partial differential equation. Due to the difculty in nding exact solu-
tions to most problems of interest, various approximate methods have been proposed [8]. If
the inverse potential, which can be viewed as a potential well, furnishes a well-dened bound
state problem, the QNMs can be evaluated by solving the associated Schrödinger equation. In
particular, when a smooth potential well can be approximated by the Pöschl-Teller potential,
QNM frequencies can be obtained through the known bound states [9]. For general potential
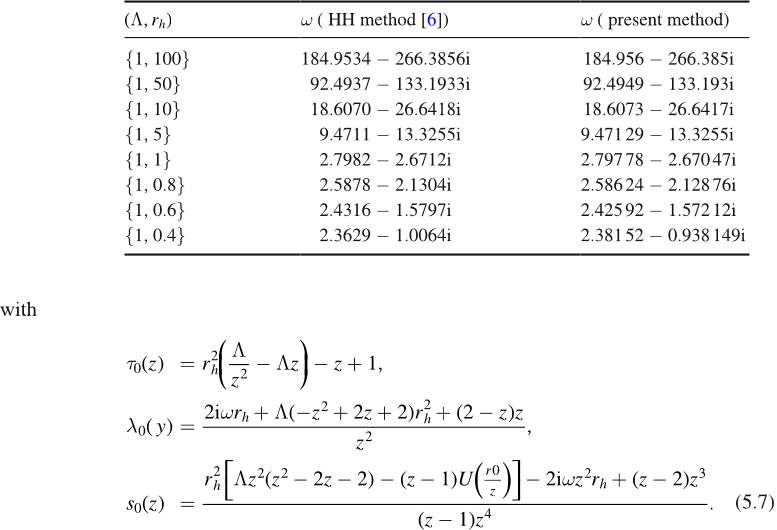
function, approaches such as continued fraction method [10], Horowitz and Hubeny (HH)
method [6], asymptotic iteration method [11] can be utilized. A common feature of the above
methods is that the corresponding master eld equationis obtained by representing the wave
function with power series. Higher precision is therefore achieved by considering higher order
expansions. A semi-analytic technique to obtain the low-lying QNMs is based on a match-
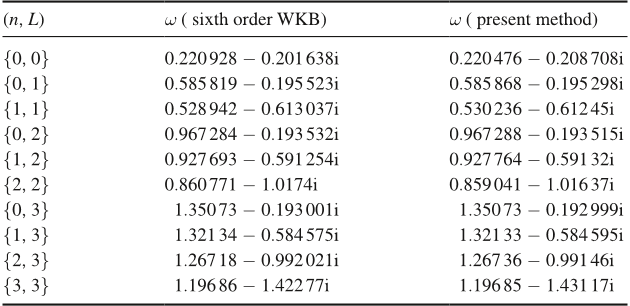
ing of the asymptotic WKB solutions at spatial innity and on the event horizon [12]. The
WKB formula has been extended to the sixth order [13]. Further generalization to a higher
order, however, is not straightforward. Finite difference method is developed to numerically
integrate the master eld equation[14], and the temporal evolution of the perturbation can be
obtained.
In this work, by discretizing the linear partial different equation[1], we transfer the mas-
ter eld equationas well as its boundary conditions into a homogeneous matrix equation. In
our approach, the master eld equationis presented in terms of linear equationsdescribing
K Lin and W-L Qian
Class. Quantum Grav. 34 (2017) 095004

3
N discretized points where the wave function is expanded up to Nth order for each of these
points. This leads to a non-standard eigenvalue problem and can be solved numerically for
the quasinormal frequencies. The present paper is organized as follows. In the next section,
we briey review how to reformulate the master eld equation in terms of a matrix equa-
tionof non-standard eigenvalue problem. In sections3 to 5, we investigate the quasinormal
modes of Schwarzschild, Schwarzschild de Sitter and Schwarzschild anti- de Sitter black hole
spacetime respectively. The precision and efciency of the present approach are studied by
comparing to the results obtained by other methods. Discussions and speculations are given
in the last section.
2. Matrix method and the eigenvalue problem for quasinormal modes
Recently, we proposed a non-grid-based interpolation scheme which can be used to solve the
eigenvalue problem [1]. A key step of the method is to formally discretize the unknown eigen-
function in order to transform a differential equationas well as the boundary conditions into a
homogeneous matrix equation. Based on the information about N scattered data point, Taylor
series are carried out for the unknown eigenfunction up to Nth order for each discretized point.
Then the resulting homogeneous system of linear algebraic equationsis solved for the eigen-
value. Here, we briey describe the discretization procedure. For a univariate function f(x),
one applies the Taylor expansion of a function to N − 1 discrete points in a small vicinity of
another point. Without loss of generality, let us expand the function about x
2
to
xxxx,,,,
N13 4
,
and therefore obtains N − 1 linear relations between function values and their derivatives as
follows
F∆=MD,
(2.1)
where
(()()()()()()()())
F
∆= −− −−
fx fx fx fx fx fx fx fx
,,,,,,
jN
T
1232
22
(2.2)
=
−
−−−
−
−
−−−
−
−
−−−
−
−
−−−
−
−
−
−
−
⎛
⎝
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎞
⎠
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
M
xx
xx xx
i
xx
N
xx
xx xx
i
xx
N
xx
xx xx
i
xx
N
xx
xx xx
i
xx
N
2! 1!
2! 1!
2! 1!
2! 1!
,
iN
iN
j
jj
i
j
N
N
NN
i
N
N
12
12
2
12 12
1
32
32
2
32 32
1
2
2
2
22
1
2
2
2
22
1
() ()
()
()
() ()
()
()
() ()
()
()
()()
()
()
(2.3)
(()()()())
() ()
″
=
′
Dfxfxfxfx,,,,
,.
kN
T
22
22
(2.4)
Now, the above equationimplies that all the derivatives at x = x
2
can be expressed in terms of
the function values by using the Cramer’s rule. In particular, we have
() ()/()
() ()/()
″
=
=
′
fx MM
fx
MM
detdet ,
detdet
,
21
22
(2.5)
K Lin and W-L Qian
Class. Quantum Grav. 34 (2017) 095004

4
where M
i
is the matrix formed by replacing the ith column of M by the column vector
F∆
.
Now, by permuting the N points,
xx x,, ,
N12
, we are able to rewrite all the derivatives at the
above N points as linear combinations of the function values at those points. Substituting the
derivatives into the eigenequation, one obtains N equationswith
() ()fx fx,,
N1
as its vari-
ables. It was shown [1] that the boundary conditions can be implemented by properly replac-
ing some of the above equations. Usually, the equations which are closer to the boundary
of the problem are chosen to be replaced, since those equationsare the least precise ones.
For instance, in the case of asymptotically at Schwarzschild spacetime below, we choose to
replace the rst and the last line in the matrix equationand implement the boundary condition
by replacing equation(3.11) with equation(3.13).
Now we apply the above method to investigate the master eld equationof for QNM. For
simplicity, here we only investigate the scalar perturbation in black hole spacetime. According
to the action of the massless scalar eld with minimal coupling in curved four dimensional
spacetime:
()
L
∫∫
=−=−∂Φ∂Φ
µ
µ
Sx
gxgdd
,
44
(2.6)
the equationof motion for the massless scalar eld reads
∇∇Φ=
µν
µν
g 0.
(2.7)
Consider the following static spherical metric
()
()
()θθ
ϕ=− ++ +sFrt
r
Fr
r
dd
d
dsin
d,
22
2
22
22
(2.8)
and rewriting the scalar eld by using the separation of variables ()
()
θ
Φ=
φ
ωϕ
−+
Y e
r
r
tmii
, we
obtain the following well-known Schrödinger-type equation
[()]
φ
ωφ
+− =
∗
r
Vr
d
d
0
2
2
2
(2.9)
where
()
() ()
() ()
=+
+
′
V
rFr
Fr
r
LL
r
1
2
is the effective potential, and
()
∫
=
∗
r
r
Fr
d
is tortoise coordi-
nate. As discussed below, the boundary conditions in asymptotically at, de Sitter and anti-de
Sitter spacetimes are different. For the interpolation in equation(2.5) to be valid, appropriate
coordinate transformation shall be introduced, which will be discussed in detail in the follow-
ing sections.
3. Quasinormal modes in Schwarzschild black hole spacetime
In Schwarzschild spacetime, one has
()=−
Fr
M
r
1
2
,
(3.1)
and r
h
= 2M corresponds to the event horizon of the black hole. The potential vanishes on
the horizon F(r
h
) = 0 and at innity
→ ∞r
, therefore, the wave function has the asymptotic
solution
()
()
φ
∼
∫
ω±
r e
i
r
Fr
d
, where ± correspond to the wave travelling in positive and negative
direction respectively. Since the wave function must be an ingoing wave on the horizon and an
outgoing wave at innity, the boundary conditions of equation(2.9) read
K Lin and W-L Qian
Class. Quantum Grav. 34 (2017) 095004