A Matrix Method for Quasinormal Modes: Schwarzschild Black Holes in Asymptotically Flat and (Anti-) de Sitter Spacetimes

TL;DR: In this article, the quasinormal modes of Schwarzschild and Schwarzschild (Anti-) de Sitter black holes were studied by a matrix method, which involves discretizing the master field equation and expressing it in form of a homogeneous system of linear algebraic equations.

Abstract: In this work, we study the quasinormal modes of Schwarzschild and Schwarzschild (Anti-) de Sitter black holes by a matrix method. The proposed method involves discretizing the master field equation and expressing it in form of a homogeneous system of linear algebraic equations. The resulting homogeneous matrix equation furnishes a non-standard eigenvalue problem, which can then be solved numerically to obtain the quasinormal frequencies. A key feature of the present approach is that the discretization of the wave function and its derivatives are made to be independent of any specific metric through coordinate transformation. In many cases, it can be carried out beforehand which in turn improves the efficiency and facilitates the numerical implementation. We also analyze the precision and efficiency of the present method as well as compare the results to those obtained by different approaches.

Summary

1. Introduction

• The second stage consists of a long period dominated by the quasinormal oscillations, where the amplitude of the oscillation decays exponentially in time.
• Mathematically, the QNMs are governed by the linearized equations of general relativity constraining perturbations around a black hole solution.
• Due to the difficulty in finding exact solutions to most problems of interest, various approximate methods have been proposed [8].
• In their approach, the master field equation is presented in terms of linear equations describing 3 N discretized points where the wave function is expanded up to Nth order for each of these points.

2. Matrix method and the eigenvalue problem for quasinormal modes

• Recently, the authors proposed a non-grid-based interpolation scheme which can be used to solve the eigenvalue problem [1].
• Based on the information about N scattered data point, Taylor series are carried out for the unknown eigenfunction up to Nth order for each discretized point.
• It was shown [1] that the boundary conditions can be implemented by properly replacing some of the above equations.
• In the case of asymptotically flat Schwarzschild spacetime below, the authors choose to replace the first and the last line in the matrix equation and implement the boundary condition by replacing equation (3.11) with equation (3.13).
• Now the authors apply the above method to investigate the master field equation of for QNM.

4. Quasinormal modes in Schwarzschild de Sitter black hole spacetime

• Now the authors are in the position to utilize the same numerical procedure to discretize the wave function in the interval ⩽ ⩽y0 1, and solve for the quasinormal frequencies.
• The obtained the quasinormal frequencies are presented in table 2 compared to those obtained by the WKB method.
• It is found that the results from the present method are consistent with those from the WKB method.

5. Quasinormal modes in in Schwarzschild anti-de Sitter black hole spacetime

• 10 Again, the eigenequation can be obtained following the same procedures as before.
• The calculated quasinormal frequencies are shown in table 3 and compared with the results obtained by the HH method.
• It is inferred from the results that the present method is in accordance with the HH method.

6. Discussions and outlooks

• The authors proposed a new interpolation scheme to discretize the master field equation  for the scalar quasinormal modes.
• It possesses flexibility and therefore the potential to explore some black hole metrics where the applications of other traditional methods become less straightforward.
• As an example, the quasinormal modes of a rotational black hole is characterized by, besides the quasinormal frequency ω, a second eigenvalue λ whose physical content is associated with the angular quantum number L. Its numerical solution, therefore, involves finding the two eigenvalues, ω and λ, simultaneously.
• A preliminary attempt [15] shows that the approach proposed in this work, on the other hand, can be applied straightforwardly in a more intuitive fashion.
• This procedure is identical for most calculations once the grid points are fixed, therefore the efficiency of the method can be significantly improved for such similar problems.

Figures

Figure 1. The calculated quasinormal frequencies ω and relative errors δω as a function of N. The calculations are carried out with rh = 1. The exact solutions are estimated by the results obtained with N = 40 interpolation points, which read ω = = = −n L1, 3 1.321 342 995 697 624 0.584 569 570 090 3002( ) i, ω = = = −n L2, 3 1.267 251 620 404 1664 0.992 016 434 193 0597( ) i.

Table 3. The quasinormal frequencies in asymptotically Anti de Sitter black hole spacetime obtained by the present method. The interpolation makes use of 22 points. It is compared to those obtained by HH method. Both calculations consider L = 0 and n = 0.

Table 2. The quasinormal frequencies in asymptotically de Sitter black hole spacetime obtained by the present method. The interpolation makes use of 22 points. It is compared to those obtained by sixth order WKB method. Both calculations consider rh = 1 and rc = 5.

Table 1. The quasinormal frequencies in asymptotically flat black hole spacetime obtained by the present method. The interpolation makes use of 15 points. It is compared to those obtained by sixth order WKB method. Both calculations consider rh = 1.

Full text

Classical and Quantum Gravity
PAPER
A matrix method for quasinormal modes:
Schwarzschild black holes in asymptotically flat
and (anti-) de Sitter spacetimes
To cite this article: Kai Lin and Wei-Liang Qian 2017 Class. Quantum Grav. 34 095004
View the article online for updates and enhancements.
Related content
Black hole quasinormal modes using the
asymptotic iteration method
H T Cho, A S Cornell, Jason Doukas et al.
-
Fermion perturbations in string theory
black holes
Owen Pavel Fernández Piedra and
Jeferson de Oliveira
-
Quasinormal Modes of a Noncommutative-
Geometry-Inspired Schwarzschild Black
Hole
Jun Liang
-
Recent citations
Charged scalar fields around Einstein-
power-Maxwell black holes
Grigoris Panotopoulos
-
The matrix method for black hole
quasinormal modes
Kai Lin and Wei-Liang Qian
-
Quasinormal modes of the BTZ black hole
under scalar perturbations with a non-
minimal coupling: exact spectrum
Grigoris Panotopoulos
-
This content was downloaded from IP address 186.217.236.64 on 04/07/2019 at 20:39

1
Classical and Quantum Gravity
A matrix method for quasinormal
modes: Schwarzschild black holes
inasymptotically at and (anti-)
de Sitter spacetimes
KaiLin
1
,
2
and Wei-LiangQian
2
,
3
1
Universidade Federal de Itajubá, Instituto de Física e Química, Itajubá, MG, Brazil
2
Escola de Engenharia de Lorena, Universidade de São Paulo, Lorena, SP, Brazil
3
Faculdade de Engenharia de Guaratinguetá, Universidade Estadual Paulista,
Guaratinguetá, SP, Brazil
E-mail: lk314159@hotmail.com and wlqian@usp.br
Received 11 January 2017, revised 1 March 2017
Accepted for publication 13 March 2017
Published 31 March 2017
Abstract
In this work, we study the quasinormal modes of Schwarzschild and
Schwarzschild (Anti-) de Sitter black holes by a matrix method. The proposed
method involves discretizing the master eld equationand expressing it in the
form of a homogeneous system of linear algebraic equations. The resulting
homogeneous matrix equationfurnishes a non-standard eigenvalue problem,
which can then be solved numerically to obtain the quasinormal frequencies.
A key feature of the present approach is that the discretization of the wave
function and its derivatives is made to be independent of any specic metric
through coordinate transformation. In many cases, it can be carried out
beforehand, which in turn improves the efciency and facilitates the numerical
implementation. We also analyze the precision and efciency of the present
method as well as compare the results to those obtained by different approaches.
Keywords: quasinormal modes, black hole, Schwarzschild spacetime,
deSitter spacetime
(Some guresmay appear in colour only in the online journal)
1. Introduction
A black hole, long considered to be a physical as well as mathematical curiosity, is derived
in general relativity as a generic prediction. Through gravitational collapse, a stellar-mass
black hole can be formed at the end of the life cycle of a very massive star, when its gravity
K Lin and W-L Qian
A matrix method for quasinormal modes: Schwarzschild black holes in asymptotically flat and (anti-) de Sitter spacetimes
Printed in the UK
095004
CQGRDG
© 2017 IOP Publishing Ltd
34
Class. Quantum Grav.
CQG
1361-6382
10.1088/1361-6382/aa6643
Paper
9
1
13
Classical and Quantum Gravity
IOP
2017
1361-6382/17/095004+13$33.00 © 2017 IOP Publishing Ltd Printed in the UK
Class. Quantum Grav. 34 (2017) 095004 (13pp) https://doi.org/10.1088/1361-6382/aa6643

2
overcomes the neutron degeneracy pressure. A crucial feature of a black hole is the existence
of the event horizon, a boundary in spacetime beyond which events cannot affect an outside
observer. Despite its invisible interior, however, the properties of a black hole can be inferred
through its interaction with other matter. By quantum eld theory in curved spacetime, it is
shown that the event horizons emit Hawking radiation, with the same spectrum of black body
radiation at a temperature determined by its mass, charge and angular momentum [2]. The
latter completes the formulation of black hole thermodynamics [3], which describes the prop-
erties of a black hole in analogy to those of thermodynamics by relating mass to energy, area
to entropy, and surface gravity to temperature. Quasinormal modes (QNMs) arise as the tem-
poral oscillations owing to perturbations in black hole spacetime [5]. Owing to the energy loss
through ux conservation, these modes are not normal. Consequently, when writing the oscil-
lation in an exponential form,
()ω− texpi
, the frequency of the modes is a complex number.
The real part,
ω
R
, represents the actual temporal oscillation; and the imaginary part,
ω
I
, indi-
cates the decay rate. Therefore, these modes are commonly referred to as quasinormal. The
stability of the black hole spacetime guarantees that all small perturbation modes are damped.
Usually, QNMs can be conditionally divided into three stages. The rst stage involves a short
period of the initial outburst of radiation, which is sensitively dependent on the initial condi-
tions. The second stage consists of a long period dominated by the quasinormal oscillations,
where the amplitude of the oscillation decays exponentially in time. This stage is character-
ized by only a few parameters of the black holes, such as their mass, angular momentum, and
charge. The last stage takes place when the QNMs are suppressed by power-law or exponen-
tial late-time tails. The properties of QNMs have been investigated in the context of the AdS/
CFT correspondence [6, 7]. As a matter of fact, practically every stellar object oscillates, and
oscillations produced by very compact stellar objects and their detection are of vital impor-
tance in physics and astrophysics. In 2015, the rst observation of gravitational waves from
a binary black hole merger was reported [4]. The observation provides direct evidence of the
last remaining unproven prediction of general relativity and reconrms its prediction of space-
time distortion on the cosmic scale.
Mathematically, the QNMs are governed by the linearized equationsof general relativity
constraining perturbations around a black hole solution. The resulting master eld equationis
a linear second order partial differential equation. Due to the difculty in nding exact solu-
tions to most problems of interest, various approximate methods have been proposed [8]. If
the inverse potential, which can be viewed as a potential well, furnishes a well-dened bound
state problem, the QNMs can be evaluated by solving the associated Schrödinger equation. In
particular, when a smooth potential well can be approximated by the Pöschl-Teller potential,
QNM frequencies can be obtained through the known bound states [9]. For general potential
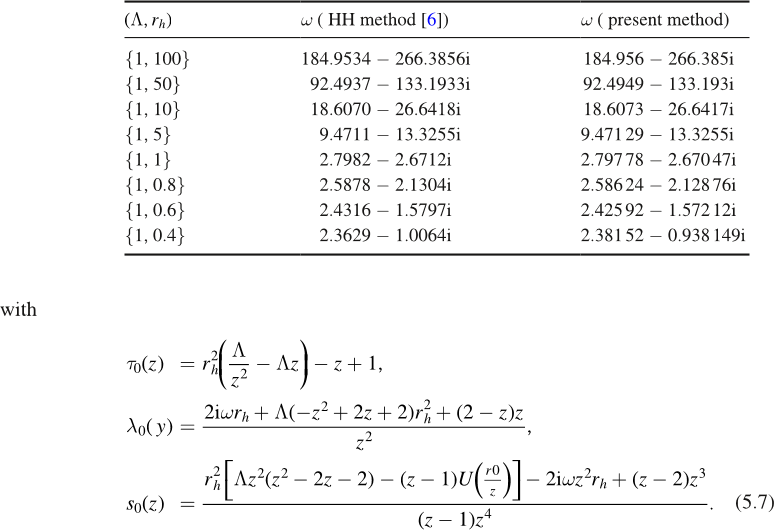
function, approaches such as continued fraction method [10], Horowitz and Hubeny (HH)
method [6], asymptotic iteration method [11] can be utilized. A common feature of the above
methods is that the corresponding master eld equationis obtained by representing the wave
function with power series. Higher precision is therefore achieved by considering higher order
expansions. A semi-analytic technique to obtain the low-lying QNMs is based on a match-
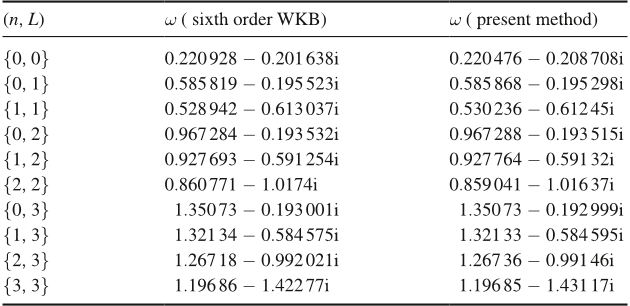
ing of the asymptotic WKB solutions at spatial innity and on the event horizon [12]. The
WKB formula has been extended to the sixth order [13]. Further generalization to a higher
order, however, is not straightforward. Finite difference method is developed to numerically
integrate the master eld equation[14], and the temporal evolution of the perturbation can be
obtained.
In this work, by discretizing the linear partial different equation[1], we transfer the mas-
ter eld equationas well as its boundary conditions into a homogeneous matrix equation. In
our approach, the master eld equationis presented in terms of linear equationsdescribing
K Lin and W-L Qian
Class. Quantum Grav. 34 (2017) 095004

3
N discretized points where the wave function is expanded up to Nth order for each of these
points. This leads to a non-standard eigenvalue problem and can be solved numerically for
the quasinormal frequencies. The present paper is organized as follows. In the next section,
we briey review how to reformulate the master eld equation in terms of a matrix equa-
tionof non-standard eigenvalue problem. In sections3 to 5, we investigate the quasinormal
modes of Schwarzschild, Schwarzschild de Sitter and Schwarzschild anti- de Sitter black hole
spacetime respectively. The precision and efciency of the present approach are studied by
comparing to the results obtained by other methods. Discussions and speculations are given
in the last section.
2. Matrix method and the eigenvalue problem for quasinormal modes
Recently, we proposed a non-grid-based interpolation scheme which can be used to solve the
eigenvalue problem [1]. A key step of the method is to formally discretize the unknown eigen-
function in order to transform a differential equationas well as the boundary conditions into a
homogeneous matrix equation. Based on the information about N scattered data point, Taylor
series are carried out for the unknown eigenfunction up to Nth order for each discretized point.
Then the resulting homogeneous system of linear algebraic equationsis solved for the eigen-
value. Here, we briey describe the discretization procedure. For a univariate function f(x),
one applies the Taylor expansion of a function to N − 1 discrete points in a small vicinity of
another point. Without loss of generality, let us expand the function about x
2
to
xxxx,,,,
N13 4
,
and therefore obtains N − 1 linear relations between function values and their derivatives as
follows
F∆=MD,
(2.1)
where
(()()()()()()()())
F
∆= −− −−
fx fx fx fx fx fx fx fx
,,,,,,
jN
T
1232
22
(2.2)
=
−
−−−
−
−
−−−
−
−
−−−
−
−
−−−
−
−
−
−
−






⎛
⎝
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎞
⎠
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
M
xx
xx xx
i
xx
N
xx
xx xx
i
xx
N
xx
xx xx
i
xx
N
xx
xx xx
i
xx
N
2! 1!
2! 1!
2! 1!
2! 1!
,
iN
iN
j
jj
i
j
N
N
NN
i
N
N
12
12
2
12 12
1
32
32
2
32 32
1
2
2
2
22
1
2
2
2
22
1
() ()
()
()
() ()
()
()
() ()
()
()
()()
()
()
(2.3)
(()()()())
() ()

″
=
′
Dfxfxfxfx,,,,
,.
kN
T
22
22
(2.4)
Now, the above equationimplies that all the derivatives at x = x
2
can be expressed in terms of
the function values by using the Cramer’s rule. In particular, we have
() ()/()
() ()/()
″
=
=
′
fx MM
fx
MM
detdet ,
detdet
,
21
22
(2.5)
K Lin and W-L Qian
Class. Quantum Grav. 34 (2017) 095004

4
where M
i
is the matrix formed by replacing the ith column of M by the column vector
F∆
.
Now, by permuting the N points,
xx x,, ,
N12
, we are able to rewrite all the derivatives at the
above N points as linear combinations of the function values at those points. Substituting the
derivatives into the eigenequation, one obtains N equationswith
() ()fx fx,,
N1
as its vari-
ables. It was shown [1] that the boundary conditions can be implemented by properly replac-
ing some of the above equations. Usually, the equations which are closer to the boundary
of the problem are chosen to be replaced, since those equationsare the least precise ones.
For instance, in the case of asymptotically at Schwarzschild spacetime below, we choose to
replace the rst and the last line in the matrix equationand implement the boundary condition
by replacing equation(3.11) with equation(3.13).
Now we apply the above method to investigate the master eld equationof for QNM. For
simplicity, here we only investigate the scalar perturbation in black hole spacetime. According
to the action of the massless scalar eld with minimal coupling in curved four dimensional
spacetime:
()
L
∫∫
=−=−∂Φ∂Φ
µ
µ
Sx
gxgdd
,
44
(2.6)
the equationof motion for the massless scalar eld reads
∇∇Φ=
µν
µν
g 0.
(2.7)
Consider the following static spherical metric
()
()
()θθ
ϕ=− ++ +sFrt
r
Fr
r
dd
d
dsin
d,
22
2
22
22
(2.8)
and rewriting the scalar eld by using the separation of variables ()
()
θ
Φ=
φ
ωϕ
−+
Y e
r
r
tmii
, we
obtain the following well-known Schrödinger-type equation
[()]
φ
ωφ
+− =
∗
r
Vr
d
d
0
2
2
2
(2.9)
where
()
() ()
() ()
=+
+
′
V
rFr
Fr
r
LL
r
1
2
is the effective potential, and
()
∫
=
∗
r
r
Fr
d
is tortoise coordi-
nate. As discussed below, the boundary conditions in asymptotically at, de Sitter and anti-de
Sitter spacetimes are different. For the interpolation in equation(2.5) to be valid, appropriate
coordinate transformation shall be introduced, which will be discussed in detail in the follow-
ing sections.
3. Quasinormal modes in Schwarzschild black hole spacetime
In Schwarzschild spacetime, one has
()=−
Fr
M
r
1
2
,
(3.1)
and r
h
= 2M corresponds to the event horizon of the black hole. The potential vanishes on
the horizon F(r
h
) = 0 and at innity
→ ∞r
, therefore, the wave function has the asymptotic
solution
()
()
φ
∼
∫
ω±
r e
i
r
Fr
d
, where ± correspond to the wave travelling in positive and negative
direction respectively. Since the wave function must be an ingoing wave on the horizon and an
outgoing wave at innity, the boundary conditions of equation(2.9) read
K Lin and W-L Qian
Class. Quantum Grav. 34 (2017) 095004