A more thorough analysis of water rockets: Moist adiabats, transient flows,
and inertial forces in a soda bottle
Cedric J. Gommes
Department of Chemical Engineering, University of Liège, B6A Allée du 6 août, 3, B-4000 Liège, Belgium
共Received 19 May 2009; accepted 12 October 2009兲
Although water rockets are widely used to illustrate first year physics principles, accurate
measurements show that they outperform the usual textbook analysis at the beginning of the thrust
phase. This paper gives a more thorough analysis of this problem. It is shown that the air expansion
in the rocket is accompanied by water vapor condensation, which provides an extra thrust; the
downward acceleration of water within the rocket also contributes to the thrust, an effect that is
negligible in other types of rockets; the apparent gravity resulting from the acceleration of the rocket
contributes as much to water ejection as does the pressure difference between the inside and outside
of the rocket; and the water flow is transient, which precludes the use of Bernoulli’s equation.
Although none of these effects is negligible, they mostly cancel each other, and the overall accuracy
of the analysis is only marginally improved. There remains a difference between theory and
experiment with water rockets. ©
2010 American Association of Physics Teachers.
关DOI: 10.1119/1.3257702兴
I. INTRODUCTION
The water rocket
1
is a popular toy that is often used in first
year physics courses to illustrate Newton’s laws of motion
and rocket propulsion. In its simplest version, a water rocket
is made of a soda bottle, a bicycle pump, a rubber stopper,
and some piping 共see Fig. 1兲. The bottle is half-filled with
water, turned upside-down, and air is pushed inside the bottle
via a flexible pipe that runs through the stopper. When the
pressure builds up, the stopper eventually pops out of the
neck. The water is then ejected and the rocket takes off.
Witnesses of the launch of a water rocket cannot but be
amazed that such a simple device can reach a height of tens
of meters in a fraction of a second.
The popularity of water rockets extends beyond physics
classrooms, with many existing associations and competi-
tions organized worldwide.
1
The more than 5000 videos
posted on YouTube with the words “water rocket” in their
title testify to their popularity. Some of these videos involve
elaborate technical developments such as multistage water
rockets, nozzles that adapt to the pressure, the replacement of
water by foam or flour, underwater rocket launches, and even
a water-propelled human flight. The public’s passionate ex-
plorations with water rockets contrast with the small number
of articles devoted to their analysis. I found only two
papers
2,3
that treat the simplest possible rocket, similar to
that shown in Fig. 1.
In the cited papers, the air expansion in the rocket is mod-
eled as an isothermal
3
or adiabatic
2
process involving dry air,
which enables the authors to estimate the pressure at any
stage of water ejection. Based on Bernoulli’s steady state
equation, the pressure is then converted to a water ejection
velocity at the nozzle, from which the thrust is estimated via
the classical equation of rocket propulsion. Finally, Newton’s
laws of motion are solved numerically to predict the flight of
the rocket. This analysis enables the time of flight to be
predicted within the experimental uncertainties of a first year
laboratory project.
3
However, more accurate measurements
with a high-speed camera show that the acceleration of the
rocket is substantially underestimated at the beginning of the
thrust phase.
2
Simple observations of water rockets hint at physical phe-
nomena that were not considered in Refs. 2 and 3. First, the
rocket is filled with fog at the end of a launch, as is visible in
the inset of Fig. 2共b兲. Water condensation is an exothermic
process that is expected to contribute positively to the thrust.
Second, the acceleration of the rocket is huge, which sug-
gests that the noninertial contribution to the apparent gravity
in the rocket might help significantly water ejection. The
rocket in Fig. 2 reaches a height of about 4 m in 0.2 s, which
implies an average acceleration of 200 m / s
2
. A more accu-
rate measurement
2
with a high-speed camera leads to an ac-
celeration of 100g’s. The flow of water is rapid not just at the
nozzle but also inside the rocket. The cloud in Fig. 2共b兲
forms at the end of ejection and appears after less than 0.2 s.
A more accurate
2
ejection time is
=0.1 s. Because the
height of water in the rocket is initially H = 10 cm, this time
converts to a velocity of U =1 m/ s inside the rocket. The
latter motion carries a momentum that may also contribute
positively to the thrust.
In this paper an analysis of the water rocket is proposed,
which takes account of the phenomena we have mentioned.
A detailed physical analysis is presented in Sec. II, and the
governing equations are derived. In Sec. III numerical solu-
tions are compared with published experimental data.
2
II. PHYSICAL ANALYSIS
A. Moist air expansion
Air expansion is the only source of energy of the rocket.
As mentioned in Sec. I, it is accompanied by vapor conden-
sation. The specific issue addressed here is the relation be-
tween the pressure P and the volume V of the expanding
moist air. This relation determines the total amount of energy
released during the ejection.
The first question is whether the expansion is adiabatic
2
or
isothermal as some authors claim.
3
For the process to be
isothermal, heat would have to diffuse into the rocket from
outside to keep the temperature constant. Generally, during a
time
, heat diffuses in air over a distance
␦
h
given by
4,5
236 236Am. J. Phys. 78 共3兲, March 2010 http://aapt.org/ajp © 2010 American Association of Physics Teachers

␦
h
2
⬇
, 共1兲
where
is the heat diffusivity of air. If we use the value
4
=0.014 cm
2
/ s and
=0.1 s, we find
␦
h
=0.04 cm. Be-
cause this distance is much smaller than the radius of the
rocket, the gas expansion has to be modeled as an adiabatic
process.
Adiabaticity does not necessarily imply that PV
␥
is a con-
stant, with
␥
=1.4 for diatomic gases.
6,7
The cooling of air
during an adiabatic expansion induces the condensation of
the water vapor it contains. Because condensation is exother-
mic, the temperature does not drop as rapidly as if the air
was dry, which keeps the pressure higher than predicted by
the PV
␥
relation. Neglecting this effect leads to an underes-
timation of the work performed by the expanding air, and
hence of the thrust.
The pressure-volume relation is derived, assuming that the
total entropy resulting from dry air, water vapor, and con-
densed water 共the fog兲 is constant during the adiabatic ex-
pansion. Assuming that air is an ideal gas, its molar entropy
s
a
is written as
6,8
s
a
共T,V兲 = s
a
共T
0
,V
0
兲 + c
V
a
ln
冋
冉
T
T
0
冊冉
V
V
0
冊
␥
−1
册
, 共2兲
where c
V
a
is the specific heat of air and V is the volume. The
0 subscript refers to any arbitrarily chosen reference state.
The molar entropy of water vapor in equilibrium with liquid
water at temperature T is written as
6,8
s
V
共T兲 = s
l
共T兲 +
⌬h
V
T
, 共3兲
where s
l
共T兲 is the molar entropy of the liquid water and ⌬h
V
is the molar enthalpy of vaporization of water. The molar
entropy of liquid water s
l
共T兲 is
6
s
l
共T兲 = s
l
共T
0
兲 + c
p
l
ln
冉
T
T
0
冊
, 共4兲
where the specific heat of water c
P
l
has been assumed to be
temperature independent.
The number of molecules in each of the three phases—air,
water vapor, and liquid water—is obtained by assuming ther-
modynamic equilibrium. This assumption implies that the
partial pressure of water vapor at any stage of the expansion
is equal to the saturating pressure P
V
共T兲. By using the ideal
gas law, P
V
共T兲 is converted to the total number of vapor
molecules N
V
in the volume V. The total number of water
molecules N
L
in the liquid is the difference between the ini-
tial and the current values of N
V
. The constant number of air
molecules in the rocket N
a
is determined as a function of the
initial pressure P
i
, volume V
i
, and temperature T
i
by sub-
tracting the contribution of water vapor to the total pressure.
The temperature-volume relation during the adiabatic ex-
pansion of moist air is obtained by conserving the total en-
tropy S= N
a
s
a
+N
V
s
v
+N
c
s
l
during the adiabatic expansion.
We use Eqs. 共2兲–共4兲 to find
冋
1−
P
V
共T
i
兲
P
i
册
c
V
ln
冉
冉
T
T
i
冊冉
V
V
i
冊
␥
−1
冊
+
冉
T
i
T
冊
⫻
冉
V
V
i
冊
P
V
共T兲
P
i
⌬h
V
T
+
P
V
共T
i
兲
P
i
冉
c
p
l
ln
冉
T
T
i
冊
−
⌬h
V
T
i
冊
=0.
共5兲
For the case of dry air, that is, for P
V
共T兲= P
V
共T
i
兲= 0, the
solution of Eq. 共5兲 is TV
共
␥
−1兲
=constant, as expected. For
moist air, however, Eq. 共5兲 has to be solved to estimate the
temperature T reached after an adiabatic expansion. Know-
ing that temperature, the corresponding pressure is obtained
by the ideal gas law.
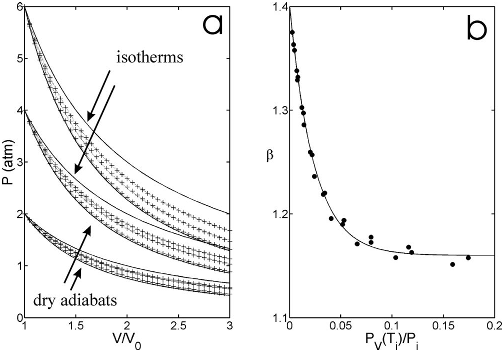
Solutions of Eq. 共5兲 are plotted in Fig. 3共a兲 for three values
of P
i
and three values of T
i
. The dry adiabats 共PV
␥
=constant兲 and isotherms 共PV=constant兲 are shown for com-
parison. The numerical values used for the calculation are
c
V
=20 J/ mol K,
8
c
P
l
=75.3 J/ mol K,
6
⌬h
V
=45 051 J/ mol,
8
and
␥
=1.4; the saturating pressure was estimated from the
Clausius–Clapeyron equation,
6–8
with P
V
共T
0
兲= 1 bar at T
0
=100 ° C.
The moist adiabats in Fig. 3共a兲 are found to be well ap-
proximated by a polytropic process
8
of the type PV

=constant 共dotted lines兲. The exponent

obtained by a least-
squares fit is found to depend mostly on the initial relative
humidity P
V
共T
i
兲/ P
i
, as shown in Fig. 3共b兲. The dependency
is well described by the empirical function
Fig. 1. In its simplest version, a water rocket is made of a soda bottle
partially filled with water, in which air is injected with a bicycle pump.
When the pressure increases, the stopper eventually pops out, water is
ejected, and the rocket takes off.
Fig. 2. Snapshots taken at times 共a兲 t =0 s, 共b兲 t=0.2 s, and t = 0.4 s during
the launch of a water rocket. The insets show the rocket at the onset of
ejection and soon after the end of ejection. Note that the ejected water in the
cloud of 共b兲 is moving upward.
237 237Am. J. Phys., Vol. 78, No. 3, March 2010 Cedric J. Gommes


= 1.15 + 共1.4 – 1.15兲exp
冉
−36
P
V
共T
i
兲
P
i
冊
, 共6兲
which reduces to

=
␥
=1.4 for dry air.
Figure 4 shows a plot of the amount of work performed by
a given volume of moist air, initially pressurized at P
i
=3, 4,
and 7 bars, when it adiabatically doubles its volume against
atmospheric pressure. In Fig. 4, the work is normalized to the
amount of work performed by dry air in the same conditions.
From Fig. 4, we see that air compressed to 3 bars performs
20% more work when it is saturated with water at 70 ° C
than when it is dry. In the experiments of Ref. 2 with P
i
=3.4 bars and P
i
=6.8 bars, and T
i
=25 ° C, the correspond-
ing exponents are estimated to be

=1.31 and

=1.35. In
both cases, the extra work resulting from water condensation
is expected to be only a few percent. The same conclusion
applies to the launches reported in Ref. 3 with P
i
=4 bars.
B. Water ejection
The determination of the rate of water ejection is a prob-
lem in fluid mechanics. The starting point of the analysis is
to assess the importance of viscous forces. Using reasoning
similar to Eq. 共1兲, the distance
␦
v
over which momentum
diffuses in a fluid during a time
due to its viscosity is
4,5
␦
V
2
⬇
, 共7兲
where
is the kinematic viscosity of the liquid. For water
4
at
20 °C,
=0.01 cm
2
/ s. Using
=0.1 s leads to
␦
v
=0.3 mm. This small value means that the flow of water out
of the rocket is not affected by viscosity, except for a sub-
millimeter thin boundary layer. Water can therefore be as-
sumed to be inviscid in this context, and ejection can be
analyzed with Euler’s equation.
The general form of Euler’s equation is
4,5
u
ជ
t
+ 共u
ជ
· ⵜ兲u
ជ
=−
1
ⵜ P + g
ជ
, 共8兲
where u
ជ
is the vector velocity of water, P is the pressure,
is
the density, and g
ជ
is the gravitational field; u
ជ
and P are gen-
erally space and time dependent. When Eq. 共8兲 is integrated
along the axis of the rocket, from the nozzle up to the free
surface of the liquid 共see Fig. 5兲, we obtain
冕
0
h
u
c
t
dz +
u
c
2
共h兲 − u
c
2
共0兲
2
+
P − P
a
+ gh =0, 共9兲
where h共t兲 is the time-dependent height of water on the axis
of the rocket, P
a
is atmospheric pressure, u
c
共h兲 is the 共nega-
tive兲 vertical velocity of the water free surface on the axis of
the rocket, and u
c
共0兲 is the exhaust velocity on the axis.
Bernoulli’s equation, as used in Refs. 2 and 3, results directly
Fig. 3. 共a兲 Pressure-volume curves of moist air during adiabatic expansion,
starting from P
i
=2, 4, and 6 bars, and initially in equilibrium with water at
T
i
=10, 50, and 90 ° C 共+兲. The solid lines are isotherms 共pV=constant兲 and
dry adiabats 共pV
␥
=constant兲. 共b兲 Moist adiabats are approximated by a
polytropic process of the form pV

=constant 关dotted lines in 共a兲兴, the expo-
nent of which is a function of the initial relative humidity.
Fig. 4. Mechanical work performed by moist air upon doubling adiabati-
cally its volume against atmospheric pressure, as a function of the initial
temperature T
i
and initial pressure P
i
=3 bars 共+兲,4bars共䊊兲, and 7 bars
共䉭兲. The work is normalized by the work performed by dry air under the
same conditions.
Fig. 5. The two reference frames used in the present analysis, and the
meaning of some symbols. The free surface of water does not remain flat if
the velocity profile is not uniform.
238 238Am. J. Phys., Vol. 78, No. 3, March 2010 Cedric J. Gommes
from Eq. 共9兲 by neglecting the time derivative as well as
gravity.
The order of magnitude of the first term in Eq. 共9兲 is
HU/
, which is equal to the magnitude of the second term
U
2
. As for the last two terms, using P − P
a
=10
5
Pa,
=1000 kg/ m
3
, H= 0.1 m, and apparent gravity g
=1000 m/ s
2
, they are found to be comparable. Therefore,
Eq. 共9兲 cannot be simplified a priori to analyze the water
rocket.
To use Eq. 共9兲 for making predictions, assumptions have
to be made about the flow pattern. We shall assume that the
velocity profiles at various heights are self-similar, that is,
u共z,r,t兲 =
dh
dt
冋
⍀共h 兲
⍀共0 兲
册
f
冉
r
R共z兲
冊
, 共10兲
where R共z兲 is the radius of the bottle at height z 共see Fig. 5兲,
⍀共z 兲=
R
2
共z兲 is the cross sectional area at height z, and f is
a function that characterizes the velocity profile and satisfies
f共0兲= 1. Uniform velocity is recovered with f共x兲= 1; the case
where the water drops more rapidly at the center of the
rocket corresponds to a function f共x兲 with a maximum at x
=0. The ratio in the square brackets in Eq. 共10兲 ensures that
the total flow of water is the same over any section of the
rocket. Moreover, the latter flow has to be equal to the rate of
air expansion. Integrating Eq. 共10兲 over a section leads to
dV
dt
=−具f典⍀共h兲
dh
dt
共11兲
with 具f典= 兰
0
1
2xf共x兲dx.
By using Eq. 共10兲, the various terms in Eq. 共9兲 can be
written explicitly as a function of h共t 兲, which leads to
I共h兲
d
dt
冉
⍀共h 兲
dh
dt
冊
+
1
2
冉
1−
冉
⍀共h 兲
⍀
0
冊
2
冊冉
dh
dt
冊
2
+
1
冉
P
i
冉
V
i
V共t兲
冊

− P
a
冊
+ gh =0 共12兲
with
I共h兲 =
冕
0
h
dz
⍀共z 兲
. 共13兲
The notation highlights that this term accounts for the inertia
of the accelerated water. In Eq. 共12兲,

is the polytropic
exponent obtained in Sec. II A and ⍀
0
=⍀共0兲 is the area of
the nozzle.
If the rocket was forced to remain immobile, Eqs. 共11兲 and
共12兲 could be solved for h共t兲 and V共t兲. When the rocket is
free to move, however, the gravity term g includes a nonin-
ertial component resulting from the rocket’s acceleration.
The water ejection can, therefore, not be predicted indepen-
dently of the rocket acceleration: the two problems are
coupled and have to be solved simultaneously.
C. Rocket acceleration
In an inertial frame immobile with respect to the ground
conservation of vertical momentum takes the form
d
dt
MU =Th−W − D, 共14兲
where the total momentum of the rocket is written as MU,
Th is the thrust, W is the weight, and D is the aerodynamic
drag. We next discuss each of these terms.
For a conventional rocket, MU is generally estimated by
assuming that the fuel moves upward at the same speed as
the rocket. This assumption does not hold for water rockets.
More generally, the total momentum is
MU = m
dZ
dt
+
冕
0
h
dz
冕
0
R共z兲
2
rdr
u共z,r,t兲, 共15兲
where m is the mass of the empty rocket, Z is its vertical
position, and u共z , r , t兲 is the velocity of the water in the
rocket. Note that, contrary to Sec. II B, the water velocity
u共z ,r, t兲 is expressed here with respect to the ground. If we
correct Eq. 共10兲 by adding dZ/ dt, Eq. 共15兲 becomes
MU = 关m +
V
w
兴
dZ
dt
+
具f典h⍀共h兲
dh
dt
, 共16兲
where V
w
=兰
0
h
⍀共z 兲dz is the volume of water in the rocket.
The second term in Eq. 共16兲 is negative; it is specific to water
rockets, and it was not taken into account in previous
studies.
2,3
This term accounts for the fact that the velocity of
water in the rocket is smaller than the velocity of the rocket
itself.
The three forces on the right-hand side of Eq. 共14兲 are
estimated in the usual way. The thrust is the rate of momen-
tum transfer out of the rocket resulting from water
expulsion.
9
By using the velocity profile in Eq. 共10兲, the
thrust takes the form
Th =
⍀共h 兲
2
⍀
0
冉
dh
dt
冊
2
具f
2
典 +
⍀共h 兲
dh
dt
dZ
dt
具f典共17兲
with 具f
2
典= 兰
0
1
2xf
2
共x兲dx. For the case of a uniform velocity
profile, the first contribution is the product of the rate of
mass loss with the exhaust velocity; the second term ac-
counts for the fact that the thrust is not estimated in the
reference frame of the rocket. The last two forces exerted on
the rocket are the weight and the aerodynamic drag. The
weight is
W = 共m +
V
w
兲g
0
, 共18兲
where g
0
is the gravity, not to be confused with g that enters
Eq. 共12兲 and includes a noninertial contribution. The aerody-
namic drag is calculated in the usual way
4,5
as
D = C
A
⍀
max
a
2
冉
dZ
dt
冊
2
, 共19兲
where
a
is the density of air, ⍀
max
is the maximum cross
section area of the rocket, and C
A
is a dimensionless drag
coefficient. For a rocket with a circular cross section and no
side wings, C
A
is about 0.75,
4
but for the following analysis,
it is sufficient to consider that its order of magnitude is 1.
Combining Eqs. 共14兲–共19兲 leads to the following differen-
tial equation:
239 239Am. J. Phys., Vol. 78, No. 3, March 2010 Cedric J. Gommes

d
dt
冋
共m +
V
w
兲
dZ
dt
+
具f典h⍀共h兲
dh
dt
册
=
⍀
2
共h兲
⍀
0
冉
dh
dt
冊
2
具f
2
典 +
⍀共h 兲
dh
dt
dZ
dt
具f典
− g
0
共m +
V
w
兲 − C
A
⍀
max
a
2
冉
dZ
dt
冊
2
, 共20兲
which expresses the conservation of vertical momentum.
Equations 共11兲, 共12兲, and 共20兲 constitute a closed system of
three differential equations that are coupled through the term
g= g
0
+d
2
Z/ dt
2
and have to be solved simultaneously for
Z共t兲, h共t兲, and V共t兲.
III. DISCUSSION
A. Numerical solutions and experimental data
In this section the predictions of Eqs. 共11兲, 共12兲, and 共20兲
are compared with the experimental data of Kagan et al.
2
which are summarized in Fig. 6. These authors used a 2-l
soda bottle as a rocket, the takeoff of which they measured
with a high-speed camera and a “smart-pulley” system.
10
Their analysis was based on a dry adiabatic expansion, on
Bernoulli’s equation, and on the estimation of the thrust as
the product mass loss rate and exhaust velocity. They also
assumed that the rocket is a cylinder with a constant section
area ⍀, ended by a sudden constriction to a smaller section
⍀
0
. The predicted height as a function of time is reproduced
in Fig. 6 as curve 0. As mentioned, the rocket outperforms
this analysis.
The discrepancy between theory and experiment is not in
contradiction with the findings of Finney,
3
according to
which the simplified analysis predicts the time of flight of the
rocket with an accuracy better than 0.2 s. Figure 6 shows that
the velocity of the rocket is underestimated only at the be-
ginning of the burnout; the velocity
v
0
at the end of the
burnout is predicted fairly accurately. As a consequence, the
remaining time of flight after the end of the burnout—
calculated, for example, as 2
v
0
/ g when drag is neglected—is
also accurately predicted. The main source of error for the
total time of flight is the duration of the burnout, which is
overestimated by less than 0.05 s for the case in Fig. 6共a兲.
Accuracy better than 0.2 s is therefore needed to detect a
discrepancy between theory and experiment on the basis of
time of flight measurements.
We have accounted for several effects which were previ-
ously not considered and which may have an important role
during the burnout. The first effect is water condensation
during air expansion, which is accounted for by a polytropic
exponent

smaller than
␥
. The second effect is the rocket
acceleration, which favors water ejection through increasing
the apparent gravity in the rocket. From dimensional analy-
sis, the acceleration is expected to be as significant as the
pressure difference between the inside and the outside of the
rocket. The third effect is the acceleration downward of the
water inside the rocket, which reduces the vertical momen-
tum of the rocket. On the other hand, water inertia is under-
estimated in the usual analysis, which makes use of Bernoul-
li’s steady equation. The transient term, proportional to I共h兲
in Eq. 共12兲, is expected to reduce the overall rocket perfor-
mance.
The procedure used for the numerical integration of Eqs.
共11兲, 共12兲, and 共20兲 is discussed in Appendix A. We shall first
assume the same rocket shape as in Ref. 2. For a perfect
cylinder, we have ⍀共h兲= ⍀
max
, and from Eq. 共13兲, I共h兲
=h / ⍀
max
. The numerical solutions for P
i
=3.4 and 6.8 bars
are plotted in Fig. 6 as curve 1 for

=1.4 共dry air兲 and 具f典
=具f
2
典=1 共a uniform velocity profile兲. For both pressures,
curve 1 is slightly above the analysis of Ref. 2, but the the-
oretical prediction remains below experiment.
A more realistic soda bottle has a transition from body to
neck, as presented in Appendix B together with the corre-
sponding values of ⍀共 h兲 and I共h兲. The corresponding solu-
tions of Eqs. 共11兲, 共12兲, and 共20兲 are shown in Fig. 6 as curve
2. Another refinement of our analysis accounts for the con-
densation of water vapor using the exponents

=1.31 and

=1.35 as calculated in Sec. II A 关see Fig. 3共b兲兴. The corre-
sponding predictions are shown in Fig. 6 as curve 3. For the
launch at P
i
=3.4 bars, the performances are slightly im-
proved by water vapor condensation, but the extra thrust is
negligible for P
i
=6.8 bars, as anticipated in Sec. II A.
The effect of a possible nonuniform velocity profile was
also investigated. The velocity profile in Eq. 共10兲 is modeled
empirically as f共x兲= exp共−0.5共x /
兲
2
兲, which amounts to as-
suming that most of the flow occurs at the center of the
rocket in a region that extends over a fraction
of its radius.
With this form of f共x兲 the coefficients 具f典 and 具f
2
典 are 具f典
=2
2
共1 − exp共−0.5/
2
兲兲 and 具f
2
典=
2
共1 − exp共−1/
2
兲兲. With
these coefficients, we found that any finite value of
results
in lower performances of the rocket, as exemplified in the
figure for
=0.5 共curve 4兲.
B. Analysis of simplified equations
Although some of the effects included in the present
analysis bring theory slightly closer to experiment, the im-
provements are small: a real rocket still outperforms the the-
oretical prediction. To try and understand why, we now con-
sider the simplified cylindrical model with ⍀共 h兲= ⍀
max
for
h⬎ 0 and I共h兲= h / ⍀
max
. It is shown in Appendix A that grav-
ity and aerodynamic drag are negligible during the thrust
Fig. 6. Predicted and experimental heights reached by a water rocket as a
function of time for 共a兲 P
i
=3.4 bars and 共b兲 P
i
=6.8 bars: 共䊊兲 experimental
data from Ref. 2, 共0兲 textbook analysis, 共1兲 current model with simplified
geometry, 共2兲 with realistic geometry, 共3兲 with realistic geometry and vapor
condensation, and 共4兲 with realistic geometry, condensation, and nonuniform
flow.
240 240Am. J. Phys., Vol. 78, No. 3, March 2010 Cedric J. Gommes