A Multilevel Monte Carlo
Asymptotic-Preserving Particle Method for
Kinetic Equations in the Diffusion Limit
Emil Løvbak, Giovanni Samaey, and Stefan Vandewalle
Abstract
We propose a multilevel Monte Carlo method for a particle-based asymptotic-
preserving scheme for kinetic equations. Kinetic equations model transport and
collisions of particles in a position-velocity phase-space. With a diffusive scaling,
the kinetic equation converges to an advection-diffusion equation in the limit of zero
mean free path. Classical particle-based techniques suffer from a strict time-step
restriction to maintain stability in this limit. Asymptotic-preserving schemes provide
a solution to this time step restriction, but introduce a first-order error in the time step
size. We demonstrate how the multilevel Monte Carlo method can be used as a bias
reduction technique to perform accurate simulations in the diffusive regime, while
leveraging the reduced simulation cost given by the asymptotic-preserving scheme.
We describe how to achieve the necessary correlation between simulation paths at
different levels and demonstrate the potential of the approach via computational
experiments.
1 Introduction
Kinetic equations, modeling particle behavior in a position-velocity phase space,
occur in many domains. Examples are plasma physics [
4
], bacterial chemotaxis [
33
]
and computational fluid dynamics [
32
]. Many of these applications exhibit a strong
time-scale separation, leading to an unacceptably high simulation cost [
7
]. However,
one typically is only interested in computing the evolution of some macroscopic
quantities of interest. These are usually some moments of the particle distribution,
which can be computed as averages over velocity space. The time-scale at which
these quantities of interest change is often much slower than the time-scale governing
Emil Løvbak · Giovanni Samaey · Stefan Vandewalle
KU Leuven, Department of Computer Science, NUMA Section, Celestijnenlaan 200A
box 2402, 3001 Leuven, Belgium e-mail: emil.loevbak@cs.kuleuven.be, e-mail: gio-
vanni.samaey@cs.kuleuven.be, e-mail: stefan.vandewalle@cs.kuleuven.be
1

2 Emil Løvbak, Giovanni Samaey, and Stefan Vandewalle
the particle dynamics. The nature of the macroscopic dynamics depends on the
scaling of the problem, which can be either hyperbolic or diffusive [15].
The model problem considered in this work is a one-dimensional kinetic equation
of the form
∂
t
f (x,v,t) + v∂
x
f (x,v,t) = Q ( f (x,v,t)), (1)
where
f (x,v,t)
represents the distribution
f
of particles as a function of position
x ∈R
and velocity
v ∈R
as it evolves in time
t
. The left-hand side of equation
(1)
represents
transport, while
Q( f (x,v,t))
is a collision operator that results in discontinuous
velocity changes. As the collision operator, we take the BGK model [
3
], which
represents linear relaxation to an equilibrium distribution that only depends on the
position density
ρ(x,t) =
Z
f (x,v,t)dv. (2)
We introduce a parameter
ε
that represents the mean free path. When decreasing
ε
,
the average time between collisions decreases. In this paper, we consider the diffusive
scaling. In that case, we simultaneously increase the time scale at which we observe
evolution of the particle distribution, arriving at
ε∂
t
f (x,v,t) + v∂
x
f (x,v,t) =
1
ε
(ρ(x,t) − f (x, v,t)). (3)
It can be shown that when taking the limit
ε →0
, the behavior of equations of the
form (5) is fully described by the diffusion equation [25]
∂
t
ρ(x,t) = ∂
xx
ρ(x,t). (4)
The simulation of kinetic equations can be done with deterministic methods,
solving the partial differential equation (PDE) that describes evolution of the particle
distribution in position-velocity phase space. Alternatively, one can use stochastic
methods that simulate a large number of particle trajectories. Deterministic methods
become prohibitively expensive for higher dimensional applications. Particle-based
methods do not suffer from this curse of dimensionality, at the expense of introducing
a statistical error in the computed solution. The issue of time-scale separation is
present in both deterministic and stochastic methods.
One way to avoid th issue of time-scale separation, is through the use of
asymptotic-preserving methods, which aim at reproducing a scheme for the lim-
iting macroscopic equation in the limit of infinite time-scale separation. For de-
terministic discretisation methods, there is a long line of such methods. We refer
to [
2
,
5
,
6
,
10
,
14
,
19
,
20
,
21
,
22
,
23
,
24
,
26
,
27
,
28
] as a representative sample
of such methods in the diffusive scaling. The recent review paper [
15
] contains
an overview of the state of the art on asymptotic-preserving methods for kinetic
equations, and ample additional references. In the particle-based setting, only a few
asymptotic-preserving methods have been developed, mostly in the hyperbolic scal-
ing [
11
,
12
,
13
,
29
,
30
,
31
]. In the diffusive scaling, there are only of two works [
9
,
16
]
so far, to the best of our knowledge. Both methods avoid the time step restrictions
Page: 2 job: MLMCforAP macro: svmult.cls date/time: 15-Jan-2019/18:31

MLMC AP Particle Method for Kinetic Equations in the Diffusion Limit 3
caused by fast problem time-scales, at the expense of introducing a bias, which is of
order one in the time step size.
The goal of the present paper is to combine the asymptotic-preserving scheme
in [
16
] with the multilevel Monte Carlo method. Given a fixed computational budget,
a trade-off typically has to be made between a small bias and a low variance. The
former can be obtained by reducing the time step, the latter by simulating many
trajectories with large time steps. The core idea behind the multilevel Monte Carlo
method [
17
] is to reduce computational cost, by combining estimates computed
with different time step sizes. The multilevel Monte Carlo method was originally
developed in the context of stochastic processes, and has been applied to problems
across many fields, for example, finance [
17
] and data science [
1
]. The method has
also successfully been applied to simulating large PDE’s with random coefficients [
8
].
Recent work has also used multilevel Monte Carlo methods in an optimization
context [34].
The remainder of this paper is organized as follows. In Section 2, we describe the
model kinetic equation on which we will demonstrate our approach, as well as the
asymptotic-preserving Monte Carlo scheme that was introduced in [
16
]. In Section 3,
we cover the multilevel Monte Carlo method that is the core contribution of this paper.
In Section 4, we present some preliminary experimental results, demonstrating the
properties of the new scheme as well as its computational gain. Finally, in Section 5
we will summarize our main results and mention some possible future extensions.
2 Model problem and asymptotic-preserving scheme
2.1 Model equation in the diffusive limit
The model problem considered in this work is a one-dimensional kinetic equation in
the diffusive scaling of the form (5), which we rewrite as
∂
t
f (x,v,t) +
v
ε
∂
x
f (x,v,t) =
1
ε
2
(ρ(x,t) − f (x, v,t)). (5)
For ease of exposition, we restrict ourselves to the case of two discrete velocities,
v =
±1
. Then, we can write
f
+
(x,t)
and
f
−
(x,t)
to represent the distribution of particles
with respective positive and negative velocities, and
ρ(x,t) = f
+
(x,t) + f
−
(x,t)
represents the total density of particles. In this case, equation (5) simplifies to
∂
t
f
+
(x,t) +
1
ε
∂
x
f
+
(x,t) =
1
ε
2
ρ(x,t)
2
− f
+
(x,t)
∂
t
f
−
(x,t) −
1
ε
∂
x
f
−
(x,t) =
1
ε
2
ρ(x,t)
2
− f
−
(x,t)
. (6)
Page: 3 job: MLMCforAP macro: svmult.cls date/time: 15-Jan-2019/18:31

4 Emil Løvbak, Giovanni Samaey, and Stefan Vandewalle
Equation
(6)
is also known as the Goldstein-Taylor model, and can be solved using a
particle scheme. We then introduce a time step ∆t and an ensemble of P particles
X
n
p,∆t
,V
n
p,∆t
P
p=1
. (7)
The particle state (position and velocity) is represented as
(X,V )
,
p
is the particle
index (
1 ≤ p ≤P
), and
n
represents the time index, i.e.,
X
n
p,∆t
≈X
p
(n∆t)
. Equation
(6)
is then solved via operator splitting as
1. Transport step. The position of each particle is updated based on its velocity
X
n+1
p,∆t
= X
n
p,∆t
±V
n
p,∆t
∆t. (8)
2. Collision step. During collisions, each particle’s velocity is updated as:
V
n+1
p,∆t
=
(
±1/ε, with probability p
c
∆t
= ∆t/ε
2
and equal probability in the sign,
V
n
p,∆t
, otherwise.
(9)
To maintain stability, this approximation requires a time step restriction
∆t = O (ε
2
)
,
leading to unacceptably high computational costs.
2.2 Asymptotic-preserving Monte Carlo scheme
Recently, an asymptotic-preserving Monte Carlo scheme was proposed [
16
], based
on the simulation of a modified equation
∂
t
f
+
+
ε
ε
2
+ ∆t
∂
x
f
+
=
∆t
ε
2
+ ∆t
∂
xx
f
+
+
1
ε
2
+ ∆t
ρ
2
− f
+
∂
t
f
−
−
ε
ε
2
+ ∆t
∂
x
f
−
=
∆t
ε
2
+ ∆t
∂
xx
f
−
+
1
ε
2
+ ∆t
ρ
2
− f
−
. (10)
In
(10)
we have dropped the space and time dependency of
f
±
and
ρ
, for conciseness.
The model given by
(10)
reduces to
(6)
in the limit when
∆t
tends to zero, and has
an O(∆t) bias. In the limit when ε tends to zero, the equations reduce to (4).
Discretizing this equation, using operator splitting as above, again leads to a
Monte Carlo scheme. For each particle
X
p
and for each time step
n
, one time step
now consists of a transport-diffusion and a collision step:
1. Transport-diffusion step.
The position of the particle is updated based on its
velocity and a Brownian increment
X
n+1
p,∆t
= X
n
p,∆t
±
ε
ε
2
+ ∆t
∆t +
√
2∆t
r
∆t
ε
2
+ ∆t
ξ
n
p
= X
n
p,∆t
+V
n
p,∆t
∆t +
√
2∆t
p
D
∆t
ξ
n
p
, (11)
Page: 4 job: MLMCforAP macro: svmult.cls date/time: 15-Jan-2019/18:31

MLMC AP Particle Method for Kinetic Equations in the Diffusion Limit 5
in which we have taken
ξ
n
p
∼ N (0,1)
and introduced a
∆t
-dependent velocity
V
n
p,∆t
and diffusion coefficient D
∆t
:
V
n
p,∆t
=
ε
ε
2
+ ∆t
, D
∆t
=
∆t
ε
2
+ ∆t
. (12)
2. Collision step. During collisions, each particle’s velocity is updated as:
V
n+1
p,∆t
=
±
ε
ε
2
+ ∆t
, with probability p
c
∆t
=
∆t
ε
2
+ ∆t
and equal probability in the sign,
V
n
p,∆t
, otherwise.
(13)
For more details, we refer the reader to [16].
3 Multilevel Monte Carlo method
3.1 Method and notation
We want to estimate some quantity of interest
Y
that is a function of the particle
distribution
f (x,v,t)
at some specific moment
t = t
∗
in time, i.e., we are interested in
Y (t
∗
) = E[F(X(t
∗
))] =
Z Z
F(x) f (x,v,t
∗
)dxdv. (14)
Note that, in equation
(14)
, the function
F
only depends on the position
x
and not on
velocity. That is a choice we make for notational convenience, and is not essential for
the method we present. The classical Monte Carlo estimator
ˆ
Y (t
∗
)
for
(14)
is given
by
ˆ
Y (t
∗
) =
1
P
P
∑
p=1
F(X
N
p,∆t
), t
∗
= N∆t. (15)
Here,
P
denotes the number of simulated trajectories,
N
the number of simulated time
steps,
∆t
the time step size and
X
N
p,∆t
is generated by the time-discretised process
(11)
–
(13)
. Given a constrained computational budget, a trade-off has to be made
when selecting the time step size
∆t
. On the one hand, a small time step reduces the
bias of the simulation of each sampled trajectory, and thus of the estimated quantity
of interest. On the other hand, a large time step reduces the cost per trajectory,
which increases the number of trajectories that can be simulated and thus reduces
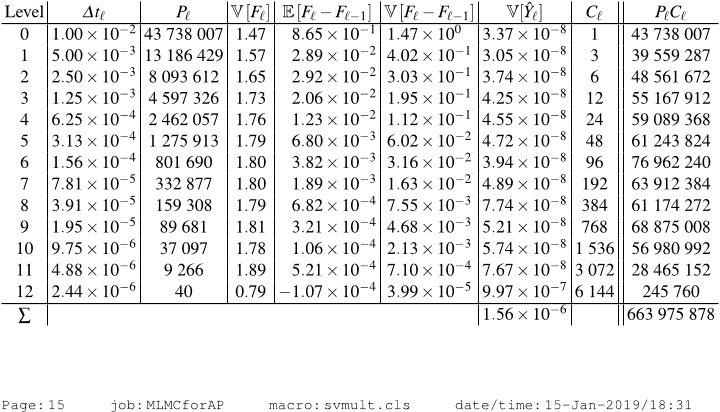
the resulting variance on the estimate. The key idea behind the Multilevel Monte
Carlo method [
17
] is to generate a sequence of estimates with varying discretization
accuracy and a varying number of realizations. The method achieves the bias of the
finest discretization, with the variance of the coarsest discretization.
Page: 5 job: MLMCforAP macro: svmult.cls date/time: 15-Jan-2019/18:31