A Multiscale Variable-grouping Framework for MRF Energy Minimization
Omer Meir Meirav Galun Stav Yagev Ronen Basri
Weizmann Institute of Science
Rehovot, Israel
{omerm, meirav.galun, stav, ronen.basri}@weizmann.ac.il
Irad Yavneh
Technion
Haifa, Israel
irad@cs.technion.ac.il
Abstract
We present a multiscale approach for minimizing the en-
ergy associated with Markov Random Fields (MRFs) with
energy functions that include arbitrary pairwise potentials.
The MRF is represented on a hierarchy of successively
coarser scales, where the problem on each scale is itself
an MRF with suitably defined potentials. These representa-
tions are used to construct an efficient multiscale algorithm
that seeks a minimal-energy solution to the original prob-
lem. The algorithm is iterative and features a bidirectional
crosstalk between fine and coarse representations. We use
consistency criteria to guarantee that the energy is non-
increasing throughout the iterative process. The algorithm
is evaluated on real-world datasets, achieving competitive
performance in relatively short run-times.
1. Introduction
In recent years Markov random fields (MRFs) have be-
come an increasingly popular tool for image modeling, with
applications ranging from image denoising, inpainting and
segmentation, to stereo matching and optical flow estima-
tion, and many more. An MRF is commonly constructed by
modeling the pixels (or regional “superpixels”) of an image
as variables that take values in a discrete label space, and by
formulating an energy function that suits the application.
An expressive model used often is the pairwise model,
which is specified by an energy function E : X → R,
E(x) =
X
v ∈V
φ
v
(x
v
) +
X
(u,v )∈E
φ
uv
(x
u
, x
v
), (1)
where x ∈ X is a label assignment of all variables v ∈ V.
The first term in this function is the sum of unary potentials,
φ
v
(x
v
), which reflect the cost of assigning label x
v
to vari-
able v. The second term is the sum of pairwise potentials,
This research was supported in part by the Israel Science Foundation
Grant No. 1265/14.
φ
uv
(x
u
, x
v
), which model the interaction between pairs of
variables by reflecting the cost of assigning labels x
u
, x
v
to
variables u, v, respectively. Here V denotes the set of vari-
ables and E is the set of pairs of interacting variables. The
inference task then is to find a label assignment that mini-
mizes the energy.
Considerable research has been reported in the literature
on approximating (1) in a coarse-to-fine framework [4, 6, 9,
11, 14, 15, 16, 17, 18]. Coarse-to-fine methods have been
shown to be beneficial in terms of running time [6, 9, 16,
18]. Furthermore, it is generally agreed that coarse-to-fine
schemes are less sensitive to local minima and can produce
higher-quality label assignments [4, 11, 16]. These benefits
follow from the fact that, although only local interactions
are encoded, the model is global in nature, and by working
at multiple scales information is propagated more efficiently
[9, 16].
Until recently, coarse-to-fine schemes were confined to
geometric structures, i.e., grouping together square patches
of variables in a grid [9, 11]. Recent works [4, 14] suggest
to group variables which are likely to end up with the same
label in the minimum energy solution, rather than by ad-
hering to a geometric structure. Such grouping may lead to
over-smoothing [6, 15]. Methods for dealing with the prob-
lem of over-smoothing include applying a multi-resolution
scheme in areas around boundaries at a segmentation task
[15, 18], or pruning the label space of fine scales with a
pre-trained classifier [6].
In this paper we present a multiscale framework for solv-
ing MRFs with multi-label arbitrary pairwise potentials.
The algorithm has been designed with the intention of opti-
mizing “hard” energies which may arise, for example, when
the parameters of the model are learned from data or when
the model accounts for negative affinities between neigh-
boring variables. Our approach uses existing inference al-
gorithms together with a variable grouping procedure re-
ferred to as coarsening, which is aimed at producing a hi-
erarchy of successively coarser representations of the MRF
problem, in order to efficiently explore relevant subsets of
the space of possible label assignments. Our method is it-

erative and monotonic, that is, the energy is guaranteed not
to increase at any point during the iterative process. The
method can efficiently incorporate any initializeable infer-
ence algorithm that can deal with general pairwise poten-
tials, e.g., QPBO-I [20] and LSA-TR [10], yielding signif-
icantly lower energy values than those obtained with stan-
dard use of these methods.
Unlike existing multiscale methods, which employ only
coarse-to-fine strategies, our framework features a bidi-
rectional crosstalk between fine and coarse representations
of the optimization problem. Furthermore, we suggest to
group variables based on the magnitude of their statistical
correlation, regardless of whether the variables are assumed
to take the same label at the minimum energy. The method
is evaluated on real-world datasets yielding promising re-
sults in relatively short run-times.
2. The multiscale framework
An inference algorithm is one which seeks a labeling of
the variables that minimizes the energy of Eq. (1). We re-
fer to the set of possible label assignments, X , as a search
space, and note that this set is of exponential size in the
number of variables. In our approach we construct a hi-
erarchy of n additional search sub-spaces of successively
lower cardinality by coarsening the graphical model. We
denote the complete search space X by X
(0)
and the hi-
erarchy of auxiliary search sub-spaces by X
(1)
, ..., X
(n)
,
with |X
(t+1)
| < |X
(t)
| for all t = 0, 1, ..., n − 1.
We furthermore associate energies with the search spaces,
E
(0)
, E
(1)
, ..., E
(n)
, with E
(t)
: X
(t)
→ R, and E
(0)
= E.
The hierarchy of search spaces is employed to efficiently
seek lower energy assignments in X .
2.1. The coarsening procedure
The coarsening procedure is a fundamental module in
the construction of coarse scales and we now describe it
in detail, see Alg. 1 for an overview. We denote the MRF
(or its graph) whose energy we aim to minimize, and its
corresponding search space by G
(0)
(V
(0)
, E
(0)
, φ
(0)
) and
X
(0)
, respectively, and use a shorthand notation G
(0)
to re-
fer to these elements. Scales of the hierarchy are denoted
by G
(t)
, t = 0, 1, 2, ..., n, such that a larger t corresponds
to a coarser scale, with a smaller graph and search space.
We next define the construction of a coarser graph
G
(t+1)
from a finer graph G
(t)
, relate between their search
spaces, and define the energy on the coarse graph. To sim-
plify notations we use u, v to denote variables (or vertices)
at level t, i.e., u, v ∈ V
(t)
, and ˜u, ˜v to denote variables at
level t + 1. A label assignment to variable u (or ˜u) is de-
noted x
u
(respectively x
˜u
). An assignment to all variables
at levels t, t + 1 is denoted by x ∈ X
(t)
and ˜x ∈ X
(t+1)
,
respectively.
Algorithm 1 [G
(t+1)
, x
(t+1)
] = COARSENING(G
(t)
, x
(t)
)
Input: Graphical model G
(t)
, optional initial labels x
(t)
Output: Coarse-scale graphical model and labels G
(t+1)
, x
(t+1)
1: x
(t+1)
← ∅
2: select a variable-grouping (Sec. 2.4)
3: set an interpolation rule f
(t+1)
: X
(t+1)
→ X
(t)
(Eq. (2),(3))
4: if x
(t)
is initialized then
5: modify f
(t+1)
to ensure monotonicity (Sec. 2.3)
6: x
(t+1)
← inherits
1
x
(t)
7: end if
8: define the coarse potentials φ
(t+1)
˜u
, φ
(t+1)
˜u˜v
(Eq. (4),(5))
9: return G
(t+1)
, x
(t+1)
Variable-grouping and graph-coarsening. To derive
G
(t+1)
from G
(t)
, we begin by partitioning the variables of
G
(t)
into a disjoint set of groups. Then, in each such group
we select one vertex to be the “seed variable” (or seed ver-
tex) of the group. As explained below, it is necessary that
the seed vertex be connected by an edge to each of the other
vertices in its group. Next, we eliminate all but the seed
vertex in each group and define the coarser graph, G
(t+1)
,
whose vertices correspond to the seed vertices of the fine
graph G
(t)
. To set the notation, let ˜v ∈ V
(t+1)
represent a
variable of G
(t+1)
, and denote by [˜v] ⊂ V
(t)
the subset of
variables of V
(t)
which were grouped to form ˜v. The col-
lection of subsets [˜v] ⊂ V
(t)
forms a partitioning of the set
V
(t)
, i.e., V
(t)
= ∪
˜v∈V
(t+1)
[˜v] and [˜u]∩[˜v] = ∅, ∀˜u 6= ˜v. In
Subsection 2.4, we shall provide details on how the group-
ings are selected.
Once the groups have been selected, the coarse-scale
graph topology is determined as follows. An edge is in-
troduced between vertices ˜u and ˜v in G
(t+1)
if there exists
at least one pair of fine-scale vertices, one in [˜u] and the
other in [˜v], that are connected by an edge. See Fig. 1 for an
illustration of variable grouping.
Interpolation rule. Next we define a coarse-to-fine inter-
polation rule, f
(t+1)
: X
(t+1)
→ X
(t)
, which maps each
labeling assignment of the coarser scale t + 1 to a labeling
of the finer scale t. We consider here only a simple inter-
polation rule, where the label of any fine variable is com-
pletely determined by the coarse-scale variable of its group
and is independent of all other coarse variables. That is,
if x = f
(t+1)
(˜x) and x
˜v
denotes the label associated with
coarse variable ˜v, then for any fine variable u ∈ [˜v], x
u
depends only on x
˜v
. More specifically, if s ∈ [˜v] is the
seed variable of the group [˜v], then the interpolation rule is
defined as follows:
i. The label assigned to the seed variable s is equal to that
1
For any coarse-scale variable ˜v, x
˜v
← x
s
, where x
s
is the label of
the seed variable of the group [˜v].

Figure 1. An illustration of variable-grouping, with seed variables denoted by black disks. Note that each seed variable is connected by an
edge to each other variable in its group, as required by the interpolation rule. Right panel: the coarse graph, whose vertices correspond to
the fine-scale seed vertices, and their coarse unary potentials account for all the internal energy potentials in their group. Edges connect
pairs of coarse-vertices according to topology at the fine scale.
of the coarse variable,
x
s
← x
˜v
. (2)
ii. Once the seed label has been assigned, the label as-
signed to any other variable in the group, u ∈ [˜v], is
that which minimizes the local energy generated by the
pair (u, s):
x
u
← arg min
x
{φ
(t)
u
(x) + φ
(t)
us
(x, x
s
)}. (3)
A single exception to this rule is elaborated in Sec. 2.3. As
we produce the coarse graph we store these interpolation as-
signments (3) in a lookup table so that they can be retrieved
when we return to the finer scale. Finally, we henceforth
use the shorthand notation x
u
|x
˜v
to denote that the interpo-
lation rule assigns the label x
u
to u ∈ [˜v] when the label of
˜v is x
˜v
.
Coarse-scale energy. The energy associated with G
(t+1)
,
denoted E
(t+1)
(˜x), depends on the interpolation rule. We
require that, for any coarse-scale labeling, the coarse-scale
energy be equal to the fine-scale energy obtained after in-
terpolation, that is, E
(t+1)
(˜x) = E
(t)
(f
(t+1)
(˜x)). We call
this consistency.
To ensure consistency, all fine potentials are accounted
for exactly once; see Fig. 1. We define the unary potential
of a coarse variable ˜v ∈ V
(t+1)
to reflect the internal fine-
scale energy of its group [˜v], according to the interpolation
rule:
φ
(t+1)
˜v
(x
˜v
) =
X
u∈[˜v]
φ
(t)
u
(x
u
|x
˜v
) + (4)
X
u,w∈[˜v]
φ
(t)
uw
(x
u
|x
˜v
, x
w
|x
˜v
).
Note that all the energy potentials of the subgraph induced
by [˜v] are accounted for in Eq. (4). The first term sums up
the unary potentials of variables in [˜v], and the second term
takes into account the energy of pairwise potentials of all
internal pairs u, w ∈ [˜v].
The pairwise potential of a coarse pair ˜u, ˜v ∈ V
(t+1)
accounts for all finer-scale pairwise potentials that have one
variable in [˜u] ⊂ V
(t)
and the other variable in [˜v] ⊂ V
(t)
,
φ
(t+1)
˜u˜v
(x
˜u
, x
˜v
) =
X
u∈[˜u]
v ∈[˜v]
φ
(t)
uv
(x
u
|x
˜u
, x
v
|x
˜v
). (5)
Note that the definition in Eq. (5) is consistent with the
topology of the graph, as was previously defined. The
coarse scale energy E
(t+1)
(˜x) is obtained by summing the
unary (4) and pairwise (5) potentials for all coarse variables
˜v ∈ V
(t+1)
and coarse pairs ˜u, ˜v ∈ V
(t+1)
.
It is readily seen that consistency is satisfied by the coars-
ening procedure, by substituting a labeling assignment of
G
(t+1)
into Eqs. (4) and (5) to verify that the energy at
scale t of the interpolated labeling is equal to the coarse-
scale energy for any interpolation rule. Consistency guar-
antees that if we reduce the coarse-scale energy, say by
applying an inference algorithm to the coarse-scale MRF,
then this reduction is translated to an equal reduction in the
fine-scale energy via interpolation. Indeed if we minimize
the coarse-scale energy and apply interpolation to this so-
lution, then we will have minimized the fine-scale energy
over the subset of fine-scale labeling assignments that are
in the range of the interpolation, i.e., all label assignments
in f
(t+1)
(X
(t+1)
) ⊂ X
(t)
.
2.2. The multiscale algorithm
The key ingredient of this paper is the multiscale al-
gorithm which takes after the classical V-cycle employed
in multigrid numerical solvers for partial differential equa-
tions [5, 21]. We describe it informally first. Our V-cycle
is driven by a standard inference algorithm, which is em-
ployed at all scales of the hierarchy, beginning with the

finest level (t = 0), traversing down to the coarsest level
(t = n), and back up to the finest level. This process com-
prises a single iteration or cycle. The cycle begins at level
t = 0 with a given label assignment. One or more itera-
tions of the inference algorithm are applied. Then, a coars-
ening step is performed: the variables are partitioned into
groups, a seed variable is selected for each group, a coarse
graph is defined and its variables inherit
1
the labels of the
seed variables. This routine of inference iterations followed
by coarsening is repeated on the next-coarser level, and so
on. Coarsening halts when the number of variables is suffi-
ciently small, say |V
(t)
| < N , and an exact solution can be
easily recovered, e.g., via exhaustive search. The solution
of the coarse scale is interpolated to scale n − 1, replac-
ing the previous solution of that scale, and some number
of inference iterations is performed. This routine of inter-
polation followed by inference is repeated to the next-finer
scale, and so on, until we return to scale 0. As noted above,
this completes a single iteration or V-cycle; see illustration
in Fig. 2. A formal description in the form of a recursive
algorithm appears in Alg. 2. Some remarks follow.
Initialization. The algorithm can be warm-started with
any choice of label assignment, x
(0)
, and with the modifi-
cations described in Sec. 2.3 it is guaranteed to maintain or
improve its energy. If an initial guess is unavailable our
algorithm readily computes a labeling in a coarse-to-fine
manner, similarly to existing works. This is done by skip-
ping the inference module that precedes a coarsening step
in the V-cycle, i.e., by skipping Step 6 of Alg. 2.
Computational complexity and choice of inference
module. The complexity of the algorithm is governed
largely by the complexity of the method used as the in-
ference module employed in Steps 6 and 11. Note that
the inference algorithm should not be run until conver-
gence, because its goal is not to find a global optimum of
the (restricted) search sub-space; rather, a small number
inference module
coarsening
interpolation
finest scale
coarsets scale
Figure 2. The multiscale V-cycle. Starting at the finest scale G
(0)
(top left circle), a label assignment is improved by an inference
algorithm (Step 6 in Alg. 2) and the graph is coarsened (denoted
by an arrow pointing downwards). This repeats until the number
of variables is sufficiently small and exact solution can be easily
recovered. The labeling is then interpolated to the next finer scale
(denoted by an arrow pointing upwards), followed by an applica-
tion of the inference algorithm. Interpolation and inference repeat
until the finest scale is reached. This process, referred to as a V-
cycle, constitutes a single iteration.
Algorithm 2 x = V-CYCLE(G
(t)
, x
(t)
, t)
Input: Graphical model G
(t)
, optional initial labels x
(t)
, t ≥ 0
Output: x
(t)
, a label assignment for all v ∈ V
(t)
1: if |V
(t)
| < N then
2: compute minimum-energy solution x
(t)
.
3: return x
(t)
4: end if
5: if x
(t)
is initialized then
6: x
(t)
← inference on G
(t)
, x
(t)
7: end if
8: G
(t+1)
, x
(t+1)
← COARSENING(G
(t)
, x
(t)
) (Alg. 1)
9: x
(t+1)
← V-CYCLE(G
(t+1)
, x
(t+1)
, t + 1) (recursive call)
10: x
(t)
← interpolate x
(t+1)
(Sec. 2.1)
11: x
(t)
← inference on G
(t)
, x
(t)
12: return x
(t)
of iterations suffice in order to obtain a label assignment
for which the interpolation rule heuristic is useful and for
which a coarsening step is therefore efficient. The inference
method must satisfy two requirements. The first is that the
method can be warm-started, otherwise each scale would
be solved from scratch without utilizing information passed
from other scales of the hierarchy, so we would lose the
ability to improve iteratively. Second, the method must be
applicable to models with general potentials. Even when
the potentials of an initial problem are of a specific type
(e.g. submodular, semi-metric), it is not guaranteed that this
property is conserved in coarser scales due to the construc-
tion of the interpolation rule (3) and to the definition of
coarse potentials (5). Subject to these limitations we use
QPBO-I [20] and LSA-TR [10] for binary models. For mul-
tilabel models we use Swap/Expand-QPBO (αβ-swap/α-
expand with a QPBO-I binary step) [20] and Lazy-Flipper
with a search depth 2 [2].
Remark. Evidently, the search space of each MRF in the
hierarchy corresponds, via the interpolation, to a search sub-
space of the next finer MRF. When coarsening, we strive to
eliminate the less likely label assignments from the search
space, whereas more likely solutions should be represented
on the coarser scale. The locally minimal energy (3) is
chosen with this purpose in mind. It is assumed heuris-
tically that a neighboring variable of the seed variable is
more likely to end up with a label that minimizes the en-
ergy associated with this pair than with any other choice.
The approximation is exact if the subgraph is a star graph.
2.3. Monotonicity
The multiscale framework described so far is not mono-
tonic, due to the fact that the initial state at a coarse level
may incur a higher energy than that of the fine state from
which it is derived. To see this, let x
(t)
denote the state at
level t, right before the coarsening stage of a V-cycle. As

noted above, coarse-scale variables inherit the current state
of seed variables. When we interpolate x
(t+1)
back to level
t, it may well be the case that the state which we get back
to is different from x
(t)
, i.e. f
(t+1)
(x
(t+1)
) 6= x
(t)
. If the
energy associated with x
(t+1)
happens to be higher than the
energy associated with x
(t)
then monotonicity is compro-
mised.
To avoid this undesirable behavior we modify the inter-
polation rule such that if x
(t+1)
was inherited from x
(t)
then
x
(t+1)
will be mapped back to x
(t)
by the interpolation.
Specifically, assume we are given a labeling
ˆ
x
(t)
at level
t. Consider every seed variable s ∈ V
(t)
and let ˜s denote its
corresponding variable in G
(t+1)
. Then, for all u ∈ [˜s] we
reset the interpolation rule (3),
x
u
|(x
˜s
= ˆx
˜s
) ← ˆx
u
, (6)
and coarse energy potentials are updated accordingly to re-
flect those changes. Now, consistency ensures that the initial
energy at level t +1, E
(t+1)
(
ˆ
x
(t+1)
), is equal to the energy
of
ˆ
x
(t)
at level t. Consequently, assuming that the inference
algorithm which is employed at every level of a V-cycle is
monotonic, the energy is non-increasing.
2.4. Variable-grouping by conditional entropy
We next describe our approach for variable-grouping and
the selection of a seed variable in each group. Heuristically,
we would like v to be a seed variable, whose labeling de-
termines that of u via the interpolation, if we are relatively
confident of what the label of u should be, given just the
label of v.
Conditional entropy measures the uncertainty in the state
of one random variable given the state of another random
variable [7]. We use conditional entropy to gauge our con-
fidence in the interpolation rule (3). Exact calculation of
conditional entropy,
H(u|v) =
X
x
u
,x
v
P
uv
(x
u
, x
v
) · log
P
v
(x
v
)
P
uv
(x
u
, x
v
)
, (7)
involves having access to the marginal probabilities of the
variables and marginalization is in general NP-hard. In-
stead, we use an approximation of the marginal probabil-
ities for pairs of variables by defining the local energy of
two variables u, v,
E
uv
(x
u
, x
v
) = φ
u
(x
u
) + φ
v
(x
v
) + φ
uv
(x
u
, x
v
). (8)
The local energy is used for the approximation of marginal
probabilities by applying the relation P r(x
u
, x
v
) =
1
Z
uv
·
exp {−E
uv
(x
u
, x
v
)}, where Z
uv
is a normalization factor,
ensuring that probabilities sum to 1.
Algorithm 3 VARIABLE-GROUPING(G
(t)
)
Input: Graphical model G
(t)
at scale t
Output: A variable-grouping of G
(t)
1: initialize: SCORES = ∅, SEEDS = ∅, VARS = V
(t)
2: for each edge (u, v) ∈ E
(t)
do
3: calculate H(u|v) for (v, u), and H(v|u) for (u, v)
4: store the (directed) pair at the respective bin in SCORES
5: end for
6: while VARS 6= ∅ do
7: pop the next edge (u, v) ∈ SCORES
// check if we can define u to be v’s seed
8: if (v ∈ VARS & u ∈ VARS ∪ SEEDS) then
9: set u to be v
0
s seed
10: SEEDS ← SEEDS ∪ {u}
11: VARS ← VARS \ {u, v}
12: end if
13: end while
Our algorithm for selecting subgraphs and their respec-
tive seed variable is described below, see also Alg. 3. First,
the local conditional entropy is calculated for all edges in
both directions. A directed edge, whose direction deter-
mines that of the interpolation, is binned in a score-list ac-
cording to its local conditional entropy score. We then pro-
ceed with the variable-grouping procedure; for each vari-
able we must determine its status, namely whether it is a
seed variable or an interpolated variable whose seed must be
determined. This is achieved by examining directed edges
one-by-one according to the order by which they are stored
in the binned-score list. For a directed edge (u, v) we ver-
ify that the intended-to-be interpolated variable v has not
been set as a seed variable nor grouped with a seed vari-
able. Similarly, we ensure that the status of the designated
seed variable u is either undetermined or that u has already
been declared a seed variable. The process terminates when
the status of all the variables has been set. As a remark,
we point to the fact that the score-list’s range is known in
advance (it is the range of feasible entropy scores) and that
no ordering is maintained within its bins. The motivation to
use a binned-score list is twofold: refrain from sorting the
score-list and thus maintain a linear complexity in the num-
ber of edges, and introduce randomization to the variable-
grouping procedure. In our experiments we fixed the num-
ber of bins to 20.
3. Evaluation
The algorithm was implemented in the framework of
OpenGM [1], a C++ template library that offers several
inference algorithms and a collection of datasets to eval-
uate on. We use QPBO-I [20] and LSA-TR [10] for bi-
nary models and Swap/Expand-QPBO (αβ-swap/α-expand
with a QPBO-I binary step) and Lazy-Flipper with a search


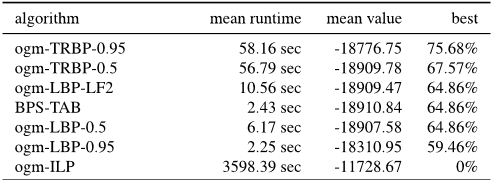
![Table 2. Performance on the Chinese Character Inpainting dataset. Five (ten) V-cycles of multiscale inference with LSA-TR reported the best energy on 40% (53%) of the dataset with outstanding runtimes. Energy and run-times are as reported in [12]. The best value can sum to more than 100% in case of ties.](/figures/table-2-performance-on-the-chinese-character-inpainting-1hecmwha.png)