A New Biometric ID-Based Cryptography Protocol and Security Analysis Using Petri Nets

About: The article was published on 2015-07-27 and is currently open access. It has received None citations till now. The article focuses on the topics: ID-based cryptography & Petri net.

Summary

Introduction

• Keywords- identity-based cryptosystem; biometrics; security analysis; cryptographic protocol; Petri nets.
• Due to the unique characteristics possessed by cryptographic protocols, analysis and evaluation tend to be more difficult than normal protocols.
• In Section 3, the authors model the client-server trust model using PN.
• Finally, the conclusions are given in Section 6.

B. Review of Proposed Protocl

• In their previous work [12], the authors have developed a new authentication protocol that allows remote mutual authentication with key agreement.
• Moreover, the new protocol is aimed to initiate secure authentication and communication between the client and server by building a robust mechanism between communicating parties.
• The following steps are necessary for the process of modelling: (a) Define the places and transitions and declare their functionalities (b) Implement a token passing scheme once the initial marking is set (c) Assess the model’s behaviour by examining reachability, boundedness, and liveness (d) Validate the model using simulation 2) Add the adversary model.
• The Petri net model in Fig. 2 represents the trust model for the proposed protocol.
• The main goal of the adversary model is to examine the protocol behaviour with the presence of an adversary while modelling attacks.

A. Analysis of Man-in-the-Middle Attack

• An active adversary A can intercept the communication line between a legitimate client and a trusted server as well as manipulate the protocol by using some means to successfully masquerade either as server or client.
• The definitions of the places and transitions used in this model are illustrated in Table 5 and Table 6, respectively.
• The adversary has the ability to control the negotiation between the client and the server.
• In fact, the adversary can clearly modify, substitute or delete all subsequent messages.

B. Analysis of Reflection Attack

• The reflection attack consists of two parties.
• Transitions are used to explicit the client and adversary actions.
• Tokens indicate the progress of the attack.
• Fig. 4 describes the execution of a reflection attack for the proposed protocol with presence of the client and adversary.
• It is obvious that, upon receiving the forged server’s response (which is in fact the adversary’s reply request), C will automatically acknowledge the response since the computation is accomplished with the correct key, so the MAC integrity check will succeed.

C. Analysis of Parallel Session Attack

• Another attack, which is effective against the proposed model without encrypted traffic, is parallel session attack.
• It involves selecting a valid combination of information from ongoing protocol executions.
• Fig. 6 explains the exploitation of parallel session attack on the proposed protocol with presence of adversary.
• The definitions of the places and the transitions for this model are defined in Table 9 and Table 10, respectively.

D. Analysis of Impersonation Attack

• Security analysis is a crucial significant process in evaluating communication and cryptographic protocols.
• The flaws within the protocol can be quickly removed via two solutions.
• Each attack scenario has been simulated using PN to exploits vulnerabilities in case if the symmetric encryption was not applied to their new protocol.
• Since the traffic is encrypted between the client and server, this proves that their new protocol is resistant to man-in-the-middle attack, reflection attack, parallel session attack, and impersonation attack.
• Also, this paper shows that replay attack and forgery attack are not effective because of the freshness property and the difficulty of creating a login request without learning any prior credentials.

Figures

Figure 3. High-level view of adversary entity attacking the protocol

Table 1. Formal Definition of a Petri Net

Figure 4. Modelling man-in-the-middle attack

Figure 5. Modelling reflection attack

Figure 1. The new proposed protocol

Table 4. DEFINITIONS OF TRANSITIONS FOR TRUST MODEL

TABLE 2. NOTATIONS USED IN THE NEW PROTOCOL

Table 3. DEFINITIONS OF PLACES FOR THE TRUST MODEL

Table 10. DEFINITIONS OF TRANSITIONS - PARALLEL SESSION ATTACK MODEL

Table 9. DEFINITIONS OF PLACES - PARALLEL SESSION ATTACK MODEL

Figure 2. The client-server trust model

Figure 6. Modelling parallel session attack

Table 5. DEFINITIONS OF TRANSITIONS - MAN-IN-THEMIDDLE ATTACK MODEL

Full text

A New Biometric ID-Based Cryptography Protocol
and Security Analysis Using Petri Nets
Dania Aljeaid
School of Science and Technology
Nottingham Trent University
Nottingham, United Kingdom
N0360890@ntu.ac.uk
Xiaoqi Ma
School of Science and Technology
Nottingham Trent University
Nottingham, United Kingdom
xiaoqi.ma@ntu.ac.uk
Caroline Langensiepen
School of Science and Technology
Nottingham Trent University
Nottingham, United Kingdom
caroline.langensiepen@ntu.ac.uk
Abstract—This paper presents a Petri net (PN) approach to
modelling, simulating, and analysing the new protocol we have
proposed. This new protocol is an enhanced authentication
scheme based on a biometric verification mechanism and identity
based cryptography. A formal approach like Petri nets allows one
to represent cryptographic protocols. For the sake of simplicity, a
complex PN model will not be discussed in this paper until all
attacks are demonstrated and the model proved to be secure.
This paper shows how Petri nets are used to model, analyse and
detect flaws in our new protocol. First, our proposed protocol is
modelled without an adversary, and then a generic adversary
model is added to examine all possible adversary behaviours.
Finally we demonstrate how Petri nets can be used to analyse
security threats such as man-in-the-middle attack, reflection
attack, and parallel session attack on this protocol.
Keywords- identity-based cryptosystem; biometrics; security
analysis; cryptographic protocol; Petri nets.
I. INTRODUCTION
Due to the unique characteristics possessed by
cryptographic protocols, analysis and evaluation tend to be
more difficult than normal protocols. Typically cryptographic
protocols, also known as security protocols, tend to inhabit a
complex environment by utilising various cryptographic
mechanisms, such as symmetric and asymmetric encryption,
hash functions, timestamps, and digital signature [1]. For this
reason, Petri nets offer the opportunity to conduct an in-depth
analysis and overcome security vulnerabilities and weaknesses.
Moreover, they simplify the modelling of exchange messages
between nodes and describe behaviour of authentication and
key agreement procedure. A number of researchers have used
Petri nets to model and analyse cryptographic protocols [2 -6].
The structure of this paper is organised as follows. In
Section 2, we briefly review previous works on Petri nets and
our new protocol. In Section 3, we model the client-server
trust model using PN. In Section 4, we add the adversary
entity to the trust model and simulate various attacks using
PN. We then provide a brief discussion on security analysis in
Section 5. Finally, the conclusions are given in Section 6.
II. REVIEW OF RELATED WORK
A. Petri Nets
The concept of the Petri net [7] was introduced in 1962 by
Carl Adam Petri [8]. Petri nets are graphical diagrammatic tools
based on strong mathematical foundations. It is used as a visual
communication aid to model concurrency, synchronisation,
limited resources, sequentially, mutual exclusion and behaviour
in distributed systems [9-11]. A Petri net is defined as a bipartite
directed, weighted graph with two types of nodes called places
and transitions, linked by directed arcs. In other words, a Petri
net must consist of the following components [9-11]:
! A set of places (drawn as circles in the graphical
representation), represent conditions and possible states
of the system.
! A set of transitions (drawn as rectangles or thick bars),
represent a change of state which caused by events or
actions
! A set of arcs (drawn as arrows), connecting a place to
transition and vice versa.
! Tokens (drawn as black dots), occupy places to
represent the truth of the associated condition.
The formal definition of a Petri net is shown in Table 1 [10].
Generally Petri nets focus on specific properties such as
liveness, deadlock, livelock, boundedness and safeness [9-11].
Table 1. Formal Definition of a Petri Net
A Petri net is 5-tuple, PN=(P,T,F,W,M
0
) where:
P={p
1
, p
2
,…,p
m
} is a finite set of places,
T={t
1
,t
2
,…,t
n
} is a finite set of transitions,
F (P X T) U (T X P) is a set of arcs (flow
relations),
W: F " {1, 2, 3,…} is a weight function,
M
0
: P " {0, 1, 2, 3,….} is the initial marking,
P ∩ T= ø and P U T ≠ ø.
A Petri net structure N=(P, T, F, W) without any specific initial
marking is denoted by N.
A Petri net with the given initial marking is denoted by (N, M
0
).
Petri nets are used in this paper to ensure the soundness of
the protocol analysis. This approach is a very useful tool for
modelling and simulating a range of possible attacks on the
proposed protocol. The key features of using Petri nets can be
summarised as follows:
1. The ability to model the concurrency of the protocol
progress with tokens
2. The ability to model intermediate and final objectives as
places

3. The ability to model transitions as commands and inputs
B. Review of Proposed Protocl
In our previous work [12], we have developed a new
authentication protocol that allows remote mutual
authentication with key agreement. Our new protocol is based
on biometric verification and ID-based Cryptograph [13].
Moreover, the new protocol is aimed to initiate secure
authentication and communication between the client and
server by building a robust mechanism between
communicating parties The proposed protocol may be
described as a two-factor user authentication mechanism and
three-way handshake procedure to establish a reliable
connection and ensure secure data sharing. Our new protocol
consists of four phases: system initialising phase, registration
phase, login phase, and authentication phase. The new protocol
is summarised in Fig. 1 and the notations used for the new
protocol are summarised in Table 2.
Registration
Client C
i
Registration Centre R
i
(1) ID
ci
, PW
ci
, Bio
ci
,
(3) ID
C
i
,
H
4
(.), Enc{}a/Dec{ }a,
f
i
, e
i
, τ, Pr_K
C
i
(2) Computes:
• f
i
= H
4
(Bio
ci
)
• e
i
= H
4
(ID
ci
||y)⊕H
4
(PW
Ci
||f
i
)
• Pr_K
ci
= (x+ H
4
(ID
c
i
))
-1
.P
Login
Client C
i
Server S
i
(1) Enters ID’
C
i
and PW’
C
i
(3) Inputs Bio’
C
i
(5) Computes:
• z’
i
= H
4
(PW
C
i
||f
i
)
• M
1
=e
i
⊕z’
i
• W
1
=r
C
i
. P
• M
2
= r
C
i
. Pr_K
C
i
• M
3
= M
1
⊕r
ci
• k=H
2
(ID
C
i
, T
C
i
, W
1
, M
2
)
(6) C
1=
Enc{ID
C
i
, T
C
i
, W
1
, M
3
,
MAC
k
(ID
C
i
, T
C
i
, W
1
,M
3
)}
a
(2)Verifies the authenticity of ID’
C
i
and
PW’
C
i
(4) Verifies
Accept if d(Bio
C
i
,
Bio
*
C
i
) < τ
Reject if d(Bio
C
i
,
Bio
*
C
i
) ≥ τ
Client C
i
Server S
i
Authentication
(5) Decrypts C
2
and verifies M
7
?=
H
4
(M
4
||r
C
i
) and the integrity of MAC
k
(ID
C
i
,
T
S
i
, W
2
, M
6
,M
7
)
Server S
i
is authenticated
(6) Computes:
• K
C
i
=r
C
i
. W
2
• Sk = H
3
(ID
C
i
, T
C
i
, T
S
i
, W
1
, W
2
, K
C
i
)
• M
8
=M
6
⊕M
1
=r
S
i
• M
9
= H
4
(M
6
||M
8
)
(4) C
2
=Enc{ID
C
i
, T
S
i
,W
2
, M
6
,
M
7
, MAC
k
(ID
C
i
, T
S
i
, W
2
, M
6
,
M
7
)}
a
(7) C
3
= Enc{M
9
, MAC
k
(M
9
)}
a
(1) Decrypts C
1
, then checks validity of ID
c
i
and freshness of T
c
i
(2) Computes:
• M
2
=(x+H
1
(ID
C
i
))
-1
.W
1
• k=H
2
(ID
C
i
, T
C
i
, W
1
, M
2
)
• Checks the integrity of MAC
k
(ID
C
i
,
T
C
i
,W
1
, M
3
)
(3) Computes:
• M
4
=H
4
(ID
C
i
||y)
• W
2
=r
S
i
.P
• K
S
i
=r
S
i
.W
1
• Sk=H
3
(ID
C
i
, T
C
i
, T
S
i
W
1
, W
2
, K
S
i
)
• M
5
=M
3
⊕M
4 =
r
C
i
• M
6
=M
4
⊕ r
S
i
• M
7
= H
4
(M
3
||M
5
)
(8) Decrypts C
3
and verifies M
9
?=
H
4
(M
6
⊕r
S
i
)
Client C
i
is authenticated
Figure 1. The new proposed protocol

TABLE 2. NOTATIONS USED IN THE NEW PROTOCOL
Symbol
Definition
C
i
User/Client /Computer
S
i
Server
R
i
Registration Centre
ID
S
i
Identity of Server
ID
C
i
Identity of user C
PW
C
i
User’s password
Bio
C
i
Biometric template of C
Pub_K
Public Key
Pr_K
Private Key
||
Message concatenation operation
P
A point on elliptic curve E with order n
xP
Denotes point multiplication on elliptic curve
y
A piece of secret information maintained by the server
(x, Pub_K
s
)
The server S’s Private/Public key pair, where
Pub_K
s
= xP
r
C
i
, r
S
i
A random number chosen by the C
i
and S
i
respectively
H(.)
A secure one-way hash function
MAC
k
(m)
The secure message authentication code of m under the
key k
XOR operation
We have examined and validated the behaviour of the
proposed protocol by using finite-state machines and Petri nets
[14]. The following steps explain the methodology to model
the proposed protocol with Petri nets:
1) Build a PN trust model of the trust relationship using
TAPAAL [15] simulation and verification software.
The following steps are necessary for the process of
modelling:
(a) Define the places and transitions and declare
their functionalities
(b) Implement a token passing scheme once the
initial marking is set
(c) Assess the model’s behaviour by examining
reachability, boundedness, and liveness
(d) Validate the model using simulation
2) Add the adversary model. This step involves the
following:
(a) Extend the original model and define places
and transitions for the adversary entities
(b) Implement the token-passing scheme with
the adversary
(c) Model different attack and identify any
insecure behaviour
III. CLIENT-SERVER TRUST MODELLED VIA PN
The trust model is a notation for determining whom the
organisations should trust with its assets. For example,
organisations usually verify the applicants’ resumes and
references, and conduct background and history checks before
trusting their employees. Once they are employed, they will be
issued photo ID badges and parking permits. In contrast to the
real world, it is challenging in the virtual world to identify
individuals who are trusted and those who are not. A trust
relationship between a client and a server can be obtained in
different practices. Some systems use the traditional way that
relies on passwords and digital certificates. Sometimes it may
involve a trusted third party to operate the authentication and
validation, such as the Kerberos login protocol [1], while other
systems deploy biometric automated verification systems to
recognise trusted users.
In the proposed trust model, the client-server trust
relationship is initiated during the registration phase. First, the
client submits his/her ID, password (PW
C
i
), and biometric data
(Bio
C
i
). Then the server will issue in return a corresponding
private key (Pr_K
C
i
), secret key (a) for the symmetric
encryption, and τ predetermined threshold for biometric
verification. The assumption for this model is that the client
and server are trustable entities, and they never cheat. Timed-
arc Petri Nets are used to model the new protocol. The trust
model consists of two Petri net entities: one for the client C
and the other for the server S. The protocol entities are derived
from the protocol description in [12]. The assumption made
for this model is that each legitimate participant is honest, i.e.
behaves according to the protocol rules. The Petri net model in
Fig. 2 represents the trust model for the proposed protocol.
The definitions of the places and transitions used in this model
are illustrated in Table 3 and Table 4, respectively.
Table 3. DEFINITIONS OF PLACES FOR THE TRUST MODEL
Place
Definition
Place
Definition
P
1
Client random number
P
14
Encrypted SYN/ACK
P
2
Client timestamp
P
15
Decrypted SYN/ACK
P
3
SYN request
P
16
Verification message
P
4
Login request
P
17
Rejected request
P
5
Encrypted login
request
P
18
Accept request – Server
is authenticated
P
6
Decrypted login req.
P
19
Session key
P
7
Verification message
P
20
ACK
P
8
Rejected request
P
21
Encrypted ACK
P
9
Accepted request
P
22
Decrypted ACK
P
10
Server random number
P
23
Verification message
P
11
Server timestamp
P
24
Rejected request
P
12
Session Key
P
25
Accept request – Client
P
13
SYN/ACK
is authenticated
Table 4. DEFINITIONS OF TRANSITIONS FOR TRUST MODEL
Trans.
Definition
Trans.
Definition
T
1
Compute login request +
SYN
T
10
Split the packet and
verify
T
2
Encrypt
T
11
Drop the packet
T
3
Decrypt
T
12
Accept
T
4
Split the packet and verify
T
13
Compute ACK and
session key
T
5
Drop the request
T
14
Encrypt ACK
T
6
Accept
T
15
Decrypt ACK
T
7
Compute SYN/ACK and
session key
T
16
Split the packet and
verify
T
8
Encrypt SYN/ACK
T
17
Drop the packet
T
9
Decrypt SYN/ACK
T
18
Accept

In the trust model, the channels between C and S are
depicted by interconnected arcs, which are attached to places.
The exchange messages procedure is represented by tokens.
Places represent storage for requests, messages, ciphers, or
session keys. Transitions in the model describe particular
functions or procedures, which may be performed while in an
execution state. For example, the following events produce a
new state: encryption, decryption, verification, and
computations. Tokens are modelled in PN as shown in Fig. 2
to represent the key agreement and message exchange
between the client and server. During simulation, the token
firing rule imitates the three-way handshake procedure. The
structure of a place linked to a transition represents a segment
of serial processes performed by the entity to fulfil its role in
the protocol run. For instance, the transition T
1
in Fig. 2
consumes three tokens from P
1
, P
2
, and P
3
to calculate the
login request. The PN trust model represents a three-way
handshake producer between C and S. It allows both C and S
to agree on a shared session key over an insecure channel. The
steps of protocol analysis for PN trust model are described as
follows:
• At first, the protocol is initiated by a client. The client
entity of the PN trust model generates a random value
(P
1
), Timestamp (P
2
), SYN request (P
3
) to compute the
login request (P
4
) within a certain period of time. C sends
the encrypted request (P
5
) to S.
• Upon receiving the request, S will check the age of the
token. Note that, computing and sending the request to S
takes some units of time. S will drop the request if the
time processing exceeds the deadline. This is guaranteed
by the use of transport arcs that preserve the age of the
tokens and the corresponding invariants.
! In the second message of the handshake, the server entity
generates a random value (P
10
), timestamp (P
11
) to
compute the session key (P
12
), and SYN/ACK request
(P
13
). Then S sends the encrypted SYN/ACK (P
14
) to C.
• Upon receiving SYN/ACK, C checks the token age and
computes the session key (P
19
). At this stage, C
authenticates S and sends an enciphered ACK (P
21
) to S.
• Finally, the server entity checks the token age and
authenticates C.
IV. TRUST MODEL WITH ADVERSARY MODELLED VIA PN
The purpose of this analysis is to find weaknesses and flaws
in the proposed protocol. It is essential to examine the
behaviour of the protocol with the presence of a malicious
adversary. An adversary entity can be a hacker, a malicious
insider, a disgruntled employee, a terrorist, organised crime, or
competitors.
Client
Server
Figure 2. The client-server trust model

The worst-case scenario would be if attackers obtained
illegitimate access to the target system. They could install
malicious software, like a rootkit, to remove or modify data.
This act of unauthorised access could lead to privilege
escalation and allow the attacker to gain elevated entry to
resources that are meant to be protected from other application
users. Moreover, faulty protocols may allow an attacker to
compromise other machines in the network to act as zombie
computers to launch denial-of-service attacks.
PN modelling is capable of mapping out how messages
flow throughout the protocol with an adversary. A high-level
view of the adversary model with information flow is shown
in Fig. 3.
The adversary entity is composed of processes, each
designed for a specific function in the protocol. Each process
models the adversary’s possible actions to capture tokens. It
can intercept messages from the channel, alter them, and pass
them to the target source.
Conceptually, the adversary entity is nondeterministic, in
that it may perform different possible actions under different
client identities at a given time to ultimately compromise the
target system. The following assumptions are considered for
the adversary model:
1) The adversary can eavesdrop, intercept, and store
messages. It may block or pass any of these
messages. Additionally, it may construct forged
messages from captured data and inject them into the
channel.
2) The adversary has zero knowledge such that it does
not possess any elements of messages transmitted
between the legitimate nodes but it can learn by
observing the traffic.
3) The traffic between client and server is not encrypted.
The main goal of the adversary model is to examine the
protocol behaviour with the presence of an adversary while
modelling attacks. In the adversary model (attack model), the
description of client and server entities is similar to the trust
model descried in section 3. For adversary entity, places
represent an adversary database, which store, control,
knowledge and accumulate all the intercepted messages.
Transitions represent a set of input events and commands the
adversary may perform to launch an attack. The input token in
the adversary entity indicates that the message has been
captured. The token movement from place to place through
the directed arcs indicates the progress of an attack. To
distinguish a genuine traffic from forged traffic, the grave
symbol ` is used to indicate that the variable could be
modified. For example, if the adversary intercepts the message
[A, B, C], the output message would be [A`, B`, C`], which
means the message has been manipulated by the adversary.
A. Analysis of Man-in-the-Middle Attack
After adding an adversary entity to the model, it can be
noticed that there is the possibility of a man-in-the-middle
between the two entities C and S. An active adversary A can
intercept the communication line between a legitimate client
and a trusted server as well as manipulate the protocol by
using some means to successfully masquerade either as server
or client. The attack model in Fig. 4 represents the man-in-the-
middle attack for the proposed protocol. The definitions of the
places and transitions used in this model are illustrated in
Table 5 and Table 6, respectively.
Table 5. DEFINITIONS OF TRANSITIONS - MAN-IN-THE-
MIDDLE ATTACK MODEL
Trans.
Definition
Trans.
Definition
T
1
Compute login request
T
13
Send forge SYN/ACK
+ SYN
T
14
Receive forge SYN/ACK
T
2
Send MSG
T
15
Split the packet and verify
T
3
Intercept MSG
T
16
Drop the request
T
4
Duplicate MSG
T
17
Accept
T
5
Send forge MSG
T
18
Compute ACK and
T
6
Received Forge MSG
session key
T
7
Split the packet and
T
19
Send ACK
verify
T
20
Intercept MSG
T
8
Drop the request
T
21
Send forge ACK
T
9
Accept
T
22
Receive forge ACK
T
10
Compute SYN/ACK
T
23
Split the packet and verify
and session key
T
24
Drop the request
T
11
Send SYN/ACK
T
25
Accept
T
12
Intercept MSG
Server
Adversary
Client
Figure 3. High-level view of adversary entity attacking the protocol

Frequently asked questions

Q1. What are the contributions in "A new biometric id-based cryptography protocol and security analysis using petri nets" ?

This paper presents a Petri net ( PN ) approach to modelling, simulating, and analysing the new protocol the authors have proposed. For the sake of simplicity, a complex PN model will not be discussed in this paper until all attacks are demonstrated and the model proved to be secure. This paper shows how Petri nets are used to model, analyse and detect flaws in their new protocol. Finally the authors demonstrate how Petri nets can be used to analyse security threats such as man-in-the-middle attack, reflection attack, and parallel session attack on this protocol. 

Q2. What is the definition of a petri net?

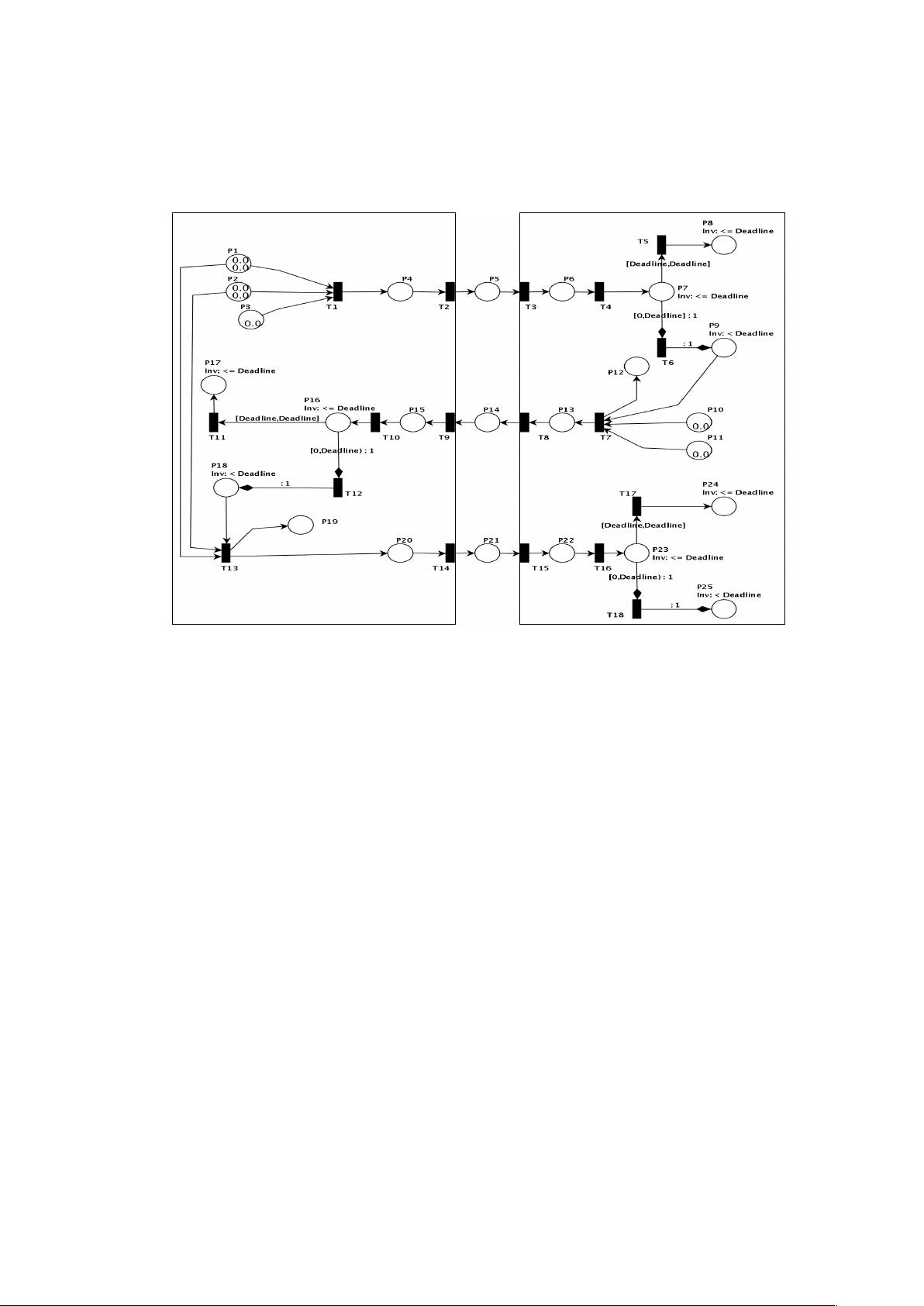
A Petri net is defined as a bipartite directed, weighted graph with two types of nodes called places and transitions, linked by directed arcs. 

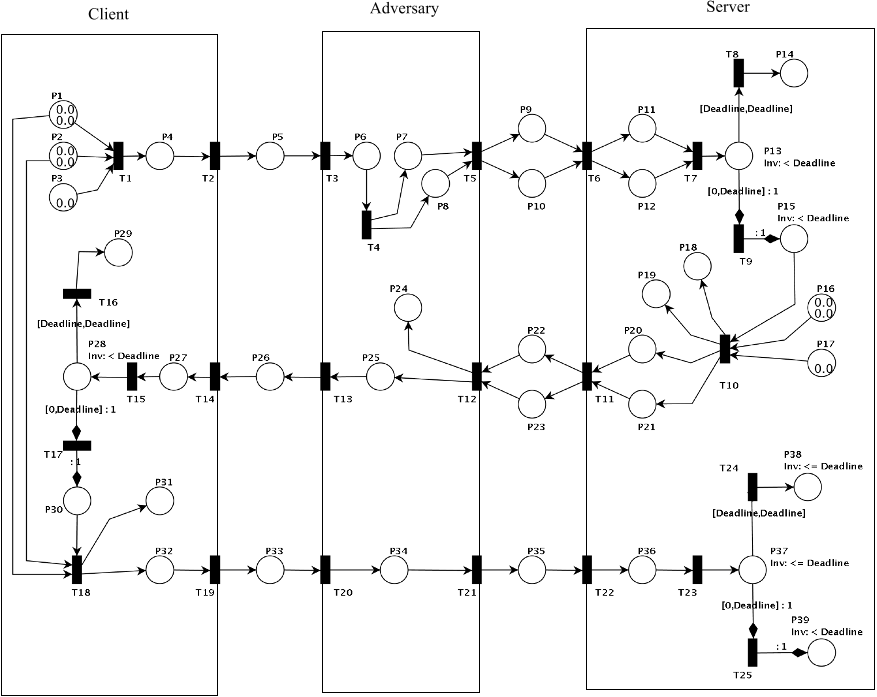
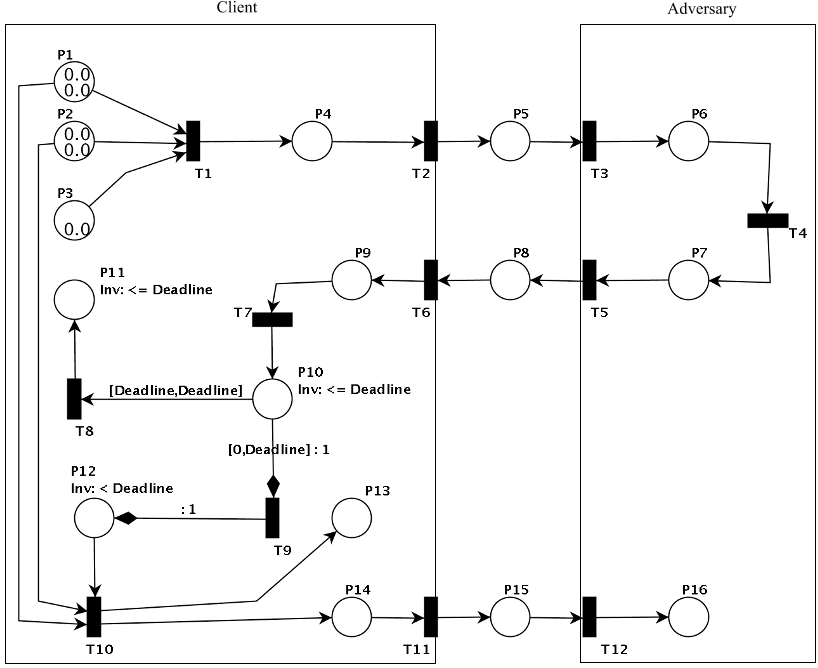
Q3. What is the main goal of the adversary model?

The main goal of the adversary model is to examine the protocol behaviour with the presence of an adversary while modelling attacks. 

Q4. What is the viable countermeasure to defend authentication attacks?

It is evident that the most viable countermeasure to defend authentication attacks is to encrypt the message exchange between the client and server. 

Q5. What is the definition of adversary entity?

the adversary entity is nondeterministic, in that it may perform different possible actions under different client identities at a given time to ultimately compromise the target system. 

Q6. What is the common type of trust relationship between a client and a server?

Sometimes it may involve a trusted third party to operate the authentication and validation, such as the Kerberos login protocol [1], while other systems deploy biometric automated verification systems to recognise trusted users. 

Q7. What is the likelihood of correlation associated with T – TC?

(1) The likelihood of correlation associated with T –̀ TC ≤ ∆T will be high considering the time-delay in widearea networks is unpredictable and varies most of the time. 

Q8. How has the PN attack been simulated?

Each attack scenario has been simulated using PN to exploits vulnerabilities in case if the symmetric encryption was not applied to their new protocol. 

Q9. What is the reason why the fabricated login request is sent to C?

A instantly impersonates C and initiates a new session with S by sending a fabricated login request: P19 = [IDA =ID`C , TA = T`S, W1=W`2, M3 = M`6, M7, MAC`k(IDC, TS, W2, M6, M7)], which is S original reply to C.Assume if the fabricated message arrives to S at time T, it will pass the verification check for the following reasons: 

Q10. What is the purpose of the attack?

To exploit the reflection attack, the adversary A intercepts the login request while listening to the electronic conversation between client C and server S. Then, the adversary sends the same login request [ID`C, T`C, W`1, M`3, MAC`k(IDC, TC, W1 ,M3)] to C in a timely manner.