A new thermodynamically consistent continuum model for hardening plasticity coupled with damage
Reads0
Chats0
TLDR
In this paper, a phenomenological model for hardening-softening elasto-plasticity coupled with damage is presented, where specific kinematic internal variables are used to describe the mechanical state of the system.About:
This article is published in International Journal of Solids and Structures.The article was published on 2002-12-01 and is currently open access. It has received 68 citations till now. The article focuses on the topics: Elastic energy & Internal energy.read more
Figures

Table 1 Comparison of experimental and numerical value of the peak stress and elastic strain for confined compressive tests on concrete, c 70; n 2; n2 3:5 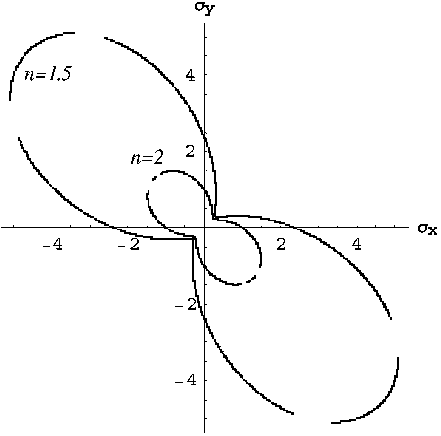
Fig. 5. Limit surface of function (53) E0 100, r0 1, n 1:5. 
Fig. 10. Uniaxial processes for n 1, 2, c 50, E 100. Mises criterion. 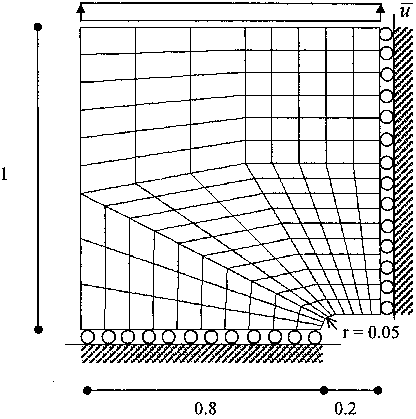
Fig. 24. Slit problem. Geometry and load condition. 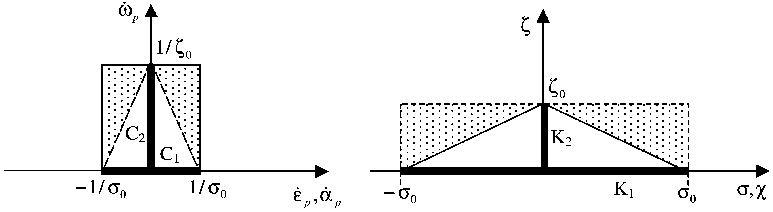
Fig. 4. Uniaxial domain C and K for Eqs. (34) and (45). 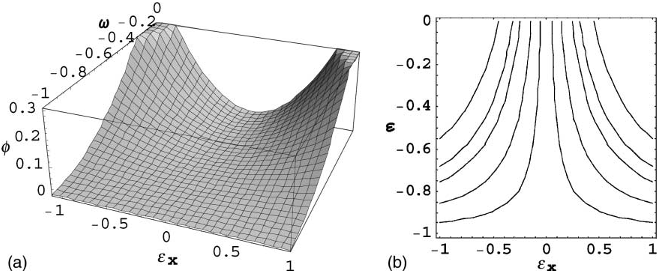
Fig. 1. Elastic potential /ðee;xeÞ and its level sets in an uniaxial case n 2.
Citations
More filters
Journal ArticleDOI
Damage-plastic model for concrete failure
Peter Grassl,Milan Jirásek +1 more
TL;DR: In this article, a triaxial damage-plastic model for the failure of reinforced concrete columns is presented, where the plasticity part is based on the effective stress and the damage model is driven by the plastic strain.
Journal ArticleDOI
At the origins and in the vanguard of peridynamics, non-local and higher-gradient continuum mechanics: An underestimated and still topical contribution of Gabrio Piola
TL;DR: Gabrio Piola's scientific papers have been underestimated in mathematical physics literature as mentioned in this paper, but a careful reading of them proves that they are original, deep and far-reaching, and even even...
Posted Content
At the origins and in the vanguard of peri-dynamics, non-local and higher gradient continuum mechanics. An underestimated and still topical contribution of Gabrio Piola
TL;DR: In this paper, the authors show that non-local and higher gradient continuum mechanics was conceived already in Piola's works and explain the reasons of the unfortunate circumstance which caused the erasure of the memory of this aspect of Piola contribution.
Journal ArticleDOI
Analytical continuum mechanics à la Hamilton-Piola least action principle for second gradient continua and capillary fluids
TL;DR: In this article, a Lagrangian action is proved to hold for capillary fluids, i.e. fluids for which the deformation energy has the form suggested, starting from molecular arguments.
Journal ArticleDOI
Dynamic problems for metamaterials: Review of existing models and ideas for further research
TL;DR: In this article, the authors focus on the design of wave-guides aimed to control wave propagation in micro-structured continua, with particular attention to piezoelectromechanical structures, having a strong coupling between macroscopic motion and some internal degrees of freedom.
References
More filters
Book
A Course on Damage Mechanics
TL;DR: In this article, the authors present a detailed analysis of the physical properties of the solid state and damage, including elasticity, deformation, shrinkage, and elasticity of the material.
Book
Mécanique des matériaux solides
TL;DR: In this paper, Rheologie, Milieux continus continus, Plasticite, and Fissuration Reference Record created on 2004-09-07, modified on 2016-08-08
Journal ArticleDOI
Strain- and stress-based continuum damage models—I. Formulation
Juan C. Simo,J.W. Ju +1 more
TL;DR: In this article, a dual framework for elastic cap damage was proposed, where a strain-and a stress-based approach was employed, and a viscous regularization of strain-based, rate-independent damage models was also developed.
Journal ArticleDOI
On energy-based coupled elastoplastic damage theories: Constitutive modeling and computational aspects
TL;DR: In this paper, an energy-based coupled elastoplastic damage theory for ductile and brittle materials is presented, which employs irreversible thermodynamics and internal state variable theory for damage.
Related Papers (5)
A framework of elastic–plastic damaging model for concrete under multiaxial stress states
Micromechanics based second gradient continuum theory for shear band modeling in cohesive granular materials following damage elasticity
Yang Yang,Anil Misra +1 more