




read more










Yet the preferred cell with minimum Rayleigh number is always expected to be one single flow cell, and with one dominating thermal cell, with an additional smaller and weaker thermal cell on the right hand side.
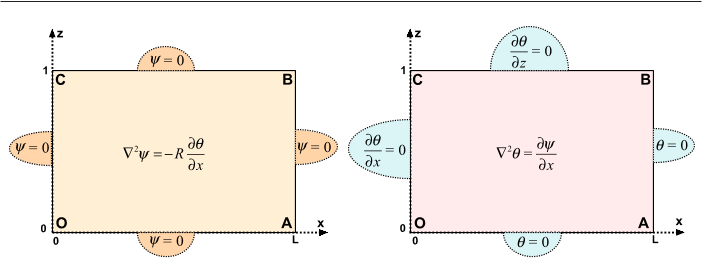
The Neumann type of impermeable/insulating conditions (Wooding 1959) and Dirichlet type of conducting walls that are open to inflow/outflow.
Since the biharmonic operator does not separate in orthogonal coordinate systems, there is no general closed-form analytical eigenfunction available, even for a rectangular geometry.
With normal modes valid over the horizontal cylinder cross-section, there is no need for normal modes in the third (vertical) direction in order to derive analytical eigenfunctions.
The assumption of 2D flow in the x, z plane isvalid also for a 3D porous medium with thickness b in the y direction, if two constraints are met: (i) The thermomechanical wall conditions at y = 0 and y = b are those of impermeable and thermally insulating walls.
Inserting the time dependency of a single oscillatory frequency changes the wave equation to a Helmholtz eigenvalue equation for the free vibrations, with the wave number as the eigenvalue.
The only modification to be made is the transformation of the local coordinates z → (z − 1), resulting in the formulaψ ∼ x(z − 1) +O(x3(z − 1)) +O(x(z − 1)3), (46)valid for the local streamfunction around the corner C.
This behavior occurs because of the mutual asymmetry between the thermomechanical conditions at x = 0 and those at x = L.A general tendency in all the Figures 2-4 is a higher concentration of streamlines than of isotherms near the right-hand side AB of the rectangle.