Noname manuscript No.
(will be inserted by the editor)
A non-normal mode marginal state of convection in
a porous rectangle
Peder A. Tyvand · Jonas Kristiansen
Nøland · Leiv Storesletten
Received: date / Accepted: date
Abstract The 4th order Darcy-B´enard eigenvalue problem for onset of ther-
mal convection in a 2D rectangular porous box is investigated. The conven-
tional type of solution has normal-mode dependency in at least one of the
two spatial directions. The present eigenfunctions are of non-normal mode
type both in the horizontal and the vertical direction. A numerical solution is
found by the finite element method, since no analytical method is known for
this non-degenerate fourth-order eigenvalue problem. All four boundaries of
the rectangle are impermeable. The thermal conditions are hand-picked to be
incompatible with normal modes: The lower boundary and the right-hand wall
are heat conductors. The upper boundary has given heat flux. The left-hand
wall is thermally insulating. The computed eigenfunctions have novel types of
complicated cell structures, with intricate internal cell walls.
1 Introduction
The onset of convection in a horizontal porous layer was first studied by Horton
and Rogers (1945) and Lapwood (1948). The reputation of this HRL problem
P. A. Tyvand
Faculty of Mathematical Sciences and Technology
Norwegian University of Life Sciences
1432
˚
As, Norway
Tel.: +47-67231564
E-mail: Peder.Tyvand@nmbu.no
J. K. Nøland
Faculty of Information Technology and Electrical Engineering
Norwegian University of Science and Technology
E-mail: Jonas.K.Noland@ntnu.no
L. Storesletten
Department of Mathematics
University of Agder
E-mail: Leiv.Storesletten@uia.no
2 Peder A. Tyvand et al.
is that it is the simplest mathematical problem of thermomechanical insta-
bility. Still there are mathematical challenges, especially those related to the
fact that the eigenvalue problem is of fourth order in space. Since the bihar-
monic operator does not separate in orthogonal coordinate systems, there is no
general closed-form analytical eigenfunction available, even for a rectangular
geometry.
In the literature on the HRL eigenvalue problem, the boundary conditions
have tacitly been restricted to make analytical solutions possible. Wooding
(1959) circumvented the restrictions of the non-separability of the biharmonic
operator for vertical porous cylinders, by a normal-mode assumption that re-
stricted the cylinder wall conditions to be equivalent to internal cell walls.
Tyvand and Storesletten (2018) verified Wooding’s normal-mode assumption
from first principles.
A normal mode is the spatial dependency of free vibrations according to
the linear wave equation. Inserting the time dependency of a single oscilla-
tory frequency changes the wave equation to a Helmholtz eigenvalue equation
for the free vibrations, with the wave number as the eigenvalue. This is the
equation valid for free vibrations of strings in 1D, of elastic membranes in
2D and for sound waves in 3D. Normal modes are thus linked to differential
equations that are of second order in space, where any choice of homogeneous
boundary conditions may fit automatically. This is not the case for higher-
order systems, where the full set of independent boundary conditions prevents
the general validity of normal modes. Still the normal modes are in common
use for analytical eigenfunctions of higher-order systems. This can only be
justified by applying degenerate boundary conditions, as was demonstrated
by Wooding (1959) for convection in a vertical porous cylinder. The details
of Wooding’s theory were carried out by Beck (1972) and Zebib (1978), for
rectangular and circular cylinders, respectively.
With normal modes valid over the horizontal cylinder cross-section, there
is no need for normal modes in the third (vertical) direction in order to de-
rive analytical eigenfunctions. This fact was demonstrated by Nield (1968, Ap-
pendix), who solved all the Dirichlet and Neumann type fourth-order problems
onset of convection in a porous medium between two horizontal planes. Wang
(1998, 1999) exemplified how the cases solved by Nield (1968) can be adjusted
to be valid for cylinders with with normal-mode compatible wall conditions.
The wave number in Nield’s solutions will then appear as the eigenvalue of
the Helmholtz equation that applies to the cross-section of the cylinder. There
are two classes of normal-mode compatible eigenvalue problems for cylinders:
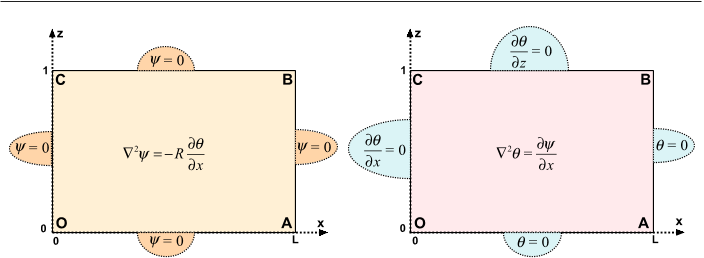
The Neumann type of impermeable/insulating conditions (Wooding 1959) and
Dirichlet type of conducting walls that are open to inflow/outflow. Barletta
and Storesletten (2015) solved the cylinder problem with these Dirichlet con-
ditions, both for a circular cross-section and an elliptical cross-section.
Non-normal modes in the horizontal direction is an interesting possibility
that was first explored by Nilsen and Storesletten (1990). Lyubimov (1975)
had suggested but not derived such solutions. To solve the problem analyt-
ically requires normal modes in the vertical direction, following Horton and
A non-normal mode marginal state of convection in a porous rectangle 3
Rogers (1945). A non-normal mode solution for a full 3D problem was given
by Haugen and Tyvand (2003), for a circular cylinder with conducting walls.
In the tangential direction, continuity and periodicity gives normal modes in
terms of the azimuthal angle coordinate. Again the analysis rested on normal
modes in the vertical direction.
What will happen to the HRL eigenvalue problem for a rectangular box
when the set of boundary conditions fails to be compatible with normal modes,
in the horizontal as well as in the vertical direction? This is the topic of the
present paper, and for simplicity we consider only a 2D rectangular box. We
hand-pick the boundary conditions so that two out of four boundaries have
conditions that are compatible with normal modes, only to be overruled by the
other boundaries that prevent normal modes from contributing to the solution.
The resulting eigenfunction is a fully non-normal mode solution in 2D, and it
can only be determined numerically, since no analytical methods are known.
When we study non-normal mode convection cells, we search for qualitative
features of the cells: The shapes of the internal cell walls, the recirculation
patterns and the relationships between streamlines and isotherms. We expect
more complicated cell patterns than the well-known HRL cell, which has a full
normal-mode type sinusoidal spatial dependency.
Earlier analytical work on the onset of convection in homogeneous and
isotropic porous rectangles has not been able to identify flow cells that have
irregular curved shapes of the internal cell walls. A tacit assumption has been
a normal-mode type of behavior either in the horizontal or vertical direction.
Thereby the cells are forced to have vertical internal cell walls, as well as
horizontal internal cell walls when higher vertical modes are taken into con-
sideration. The literature on the topic tends to assume that internal cell walls
in a marginal linearized state of convection onset in 2D rectangular porous
rectangles will always have rectangular internal cell walls, parallel to the ex-
ternal rectangular boundaries. However, this assumption has has never been
proven, and in the present paper we will demonstrate that it is incorrect.
In linearized theory of convection onset, one looks for the critical Rayleigh
number and the corresponding preferred cell width. The present numerical
solutions will produce precise Rayleigh numbers, but there will be no precise
concept of cell width. The shapes of the internal flow cells and thermal cells
will differ from one another, and their internal cell walls may have complicated
curved shapes that defy the wave number concept.
2 Mathematical formulation
A porous medium is considered, with 2D flow in the x, z plane. Physically this
corresponds to a 3D porous medium with impermeable and insulating walls
y = 0 and y = b, where the distance b is sufficiently small compared with
the vertical length scale, implying that the preferred mode of free convection
will be 2D. The z axis is directed vertically upwards. The porous medium is
homogeneous and isotropic. The assumption of 2D flow in the x, z plane is
4 Peder A. Tyvand et al.
valid also for a 3D porous medium with thickness b in the y direction, if two
constraints are met: (i) The thermomechanical wall conditions at y = 0 and
y = b are those of impermeable and thermally insulating walls. (ii) The cell
width in the x direction must be sufficiently large compared with b.
From now on we assume these conditions for 2D flow in the x, z plane to
be met without specifying them further. Storesletten and Tveitereid (1991)
investigated a problem where the range of validity of this assumption of 2D
flow has been scrutinized.
The velocity vector v has Cartesian components (u, w). The temperature
field is T (x, z, t), with t denoting time. The undisturbed motionless state has
uniform vertical temperature gradient. The gravitational acceleration g is writ-
ten in vector form as g.
The standard Darcy-Boussinesq equations for convection in a homogeneous
and isotropic porous medium can be written
∇p +
µ
K
v + ρ
0
β (T − T
0
)g = 0, (1)
∇ · v = 0, (2)
(ρc
p
)
m
∂T
∂t
+ (ρc
p
)
f
v · ∇T = λ
m
∇
2
T. (3)
In these equations, p is the dynamic pressure, β is the coefficient of thermal
expansion, ρ = ρ
0
is the fluid density at the reference temperature T
0
, µ
is the dynamic viscosity of the saturating fluid, K is the permeability, c
p
is
the specific heat at constant pressure, and λ
m
is the thermal conductivity of
the saturated porous medium. The subscript m refers to an average over the
solid/fluid mixture, while the subscript f refers to the saturating fluid alone.
We consider a 2D porous medium with a rectangular shape, bounded by
the four sides
x = 0, x = l, z = 0, z = h. (4)
The lower boundary is taken to be impermeable and perfectly heat-conducting
w = 0, T − T
0
= 0, at z = 0, (5)
while the upper boundary is taken to be impermeable and with constant uni-
form heat flux
w = 0,
∂T
∂z
= −
∆T
h
, at z = h, (6)
where ∆T is the temperature difference across the layer in its undisturbed
state. T
0
is a reference temperature The left-hand boundary is assumed to be
impermeable and thermally insulating
u = 0,
∂T
∂x
= 0, at x = 0, (7)
while the right-hand boundary is assumed to be impermeable and perfectly
conducting
u = 0, T − T
0
= −
∆T
h
z, at x = l. (8)
A non-normal mode marginal state of convection in a porous rectangle 5
These four boundary conditions are hand-picked to violate in a mild way
the requirements for normal mode solutions, both in the horizontal and the
vertical direction. These conditions are designed to be as simple as possible.
The lower and the left-hand boundary condition alone are in themselves com-
patible with normal modes. The violation of normal modes is due to the upper
boundary condition as far as the vertical dependency of the eigenfunction is
concerned. The violation of normal modes in due to the right-hand boundary
condition as far as the horizontal dependency is concerned.
The upper right-hand corner (l, h) is thus the troublesome corner where
two non-normal mode type of conditions meet. Not surprising, we will discover
small convergence problems near the upper-right hand corner, and we will ap-
ply a finer numerical grid around this corner than elsewhere in the rectangular
fluid domain.
2.1 Dimensionless equations
From now on we work with dimensionless variables. We reformulate the math-
ematical problem in dimensionless form by means of the transformations
1
h
(x, z) → (x, z),
h
κ
m
(u, w) → (u, w), h∇ → ∇,
1
∆T
(T − T
0
) → T,
K
µκ
m
(p − p
0
) → p,
(ρc
p
)
f
κ
m
(ρc
p
)
m
H
2
t → t,
(9)
where κ
m
= λ
m
/(ρ
0
c
p
)
f
is the thermal diffusivity of the saturated porous
medium. We denote the vertical unit vector by k, directed upwards.
The dimensionless governing equations can then be written
v + ∇p − R T k = 0. (10)
∇ · v = 0 (11)
∂T
∂t
+ v · ∇T = ∇
2
T, (12)
with the boundary conditions at the lower and upper boundaries
w = T = 0, z = 0, (13)
w =
∂T
∂z
+ 1 = 0, z = 1. (14)
The boundary conditions at the sidewalls are
∂T
∂x
= u = 0, x = 0, (15)
T = u = 0, x = l/h. (16)
We have introduced the Rayleigh number R defined as
R =
ρ
0
gβK∆T h
µκ
m
. (17)