HAL Id: hal-01219051
https://hal.archives-ouvertes.fr/hal-01219051
Submitted on 27 Oct 2015
HAL is a multi-disciplinary open access
archive for the deposit and dissemination of sci-
entic research documents, whether they are pub-
lished or not. The documents may come from
teaching and research institutions in France or
abroad, or from public or private research centers.
L’archive ouverte pluridisciplinaire HAL, est
destinée au dépôt et à la diusion de documents
scientiques de niveau recherche, publiés ou non,
émanant des établissements d’enseignement et de
recherche français ou étrangers, des laboratoires
publics ou privés.
A Posteriori Error Bounds for Reduced-Basis
Approximation of Parametrized Noncoercive and
Nonlinear Elliptic Partial Dierential Equations
Karen Veroy, Christophe Prud’Homme, Dimitrios V. Rovas, Anthony T.
Patera
To cite this version:
Karen Veroy, Christophe Prud’Homme, Dimitrios V. Rovas, Anthony T. Patera. A Posteriori Error
Bounds for Reduced-Basis Approximation of Parametrized Noncoercive and Nonlinear Elliptic Partial
Dierential Equations. 16th AIAA Computational Fluid Dynamics Conference, 2003, Orlando, United
States. �hal-01219051�

A Posteriori Error Bounds fo r Reduced-Basis
Approximation of Parametr ized Noncoercive
and Nonlinear Elliptic Partial Differential
Equations
K. Veroy
∗
Massachusetts Institute of Technology, Cambridge, MA 02139
C. Prud’homme
∗
D.V. Rovas
†
University of Illinois – Urbana-Champaign, Urbana, IL 61801
and A.T. Patera
∗
We present a technique for the rapid and reliable prediction of linear–functional out-
puts of elliptic partial differential equations with affine parameter dependence. The
essential components are (i ) rapidly convergent global reduced–basis approximations —
(Galerkin) projection onto a space W
N
spanned by solutions of the governing partial dif-
ferential equation at N selected points in parameter space; (ii ) a posteriori error estimation
— relaxations of the error-residual equation that provide inexpensive yet sharp bounds
for the error in the outputs of interest; and (iii ) off-line/on-line computational procedures
— methods which decouple the generation and projection stages of the approximation
process. The operation count for the on–line stage — in which, given a new parameter
value, we calculate the output of interest and associated error bound — depends only on
N (typically very small) and the parametric complexity of t he problem.
In this paper we develop new a posteriori error estimation procedures for noncoercive
linear, and certain nonlinear, problems that yield rigorous and sharp error statements for
all N . We consider three particular examples: the Helmholtz (reduced-wave) equation; a
cubically nonlinear Poisson equation; and Burgers equation — a model for incompressible
Navier-Stokes. The Helmholtz (and Burgers) example introduce our new lower bound
constructions for the requisite inf-sup (singular value) stability factor; the cubic nonlin-
earity exercises symmetry factorization procedures necessary for treatment of high-order
Galerkin summations in the (say) r esidual dual-norm calculation; and the Burgers equa-
tion illustrates our accommodation of potentially multiple solution branches in our a
posteriori error statement. Numerical results are presented that demonstrate the rigor,
sharpness, and efficiency of our proposed error bounds, and the application of these
bounds to adaptive (optimal) approximation.
1 Introduction
The optimization, control, and characterization of
an engineering component or system requires the pre-
diction of certain “quantities of interest,” or per-
formance metrics, which we shall denote outputs —
for example deflections, heat transfer rates, or drags.
These outputs are typically expressed as functionals
of field variables associated with a parametrized par-
tial differential equation which describes the physical
behavior of the component or system. The parame-
∗
Department of Mechanical Engine ering , Room 3-264
†
Department of Mechanical and Industrial Engineering, MC
244
Copyright
c
2003 by the American Institute of Aeronautics and
Astronautics, Inc. No copyright is asserted in the Uni ted States
under Title 17, U.S. Code. The U.S. Government has a royalty-
free license to exercise all rights under the copyright claimed herein
for Governmental Purposes. All other rights are reserved by the
copyright owner.
ters, which we shall denote inputs, serve to identify a
particular “configuration” of the component. We thus
arrive at an implicit input-output relationship, eval-
uation of which demands solution of the underlying
partial differential equation.
Our goal is the development of computational meth-
ods that permit rapid and reliable evaluation of this
partial-differential-equation-induced input-output re-
lationship in the limit of many queries — that is,
in the design, optimization, control, and character-
ization contexts. Our particular approach is based
on the reduced-basis method, first introduced in the
late 1970s for nonlinear structural analysis,
1, 11
and
subsequently developed more broadly in the 1980s
and 1990s.
2–4, 12, 13, 17
The reduced-basis method rec-
ognizes that the field variable is not, in fact, some
arbitrary member of the infinite-dimensional solution
space associated with the partial differential equation;
1 of 18
American Institute of Aeronautics and Astronautics Paper 2003-3847

rather, it resides, or “evolves,” on a much lower-
dimensional manifold induced by the parametric de-
pendence.
The reduced-basis approach as earlier articulated is
local in parameter space in both practice and theory.
4
As a result, the computational improvements — rela-
tive to conventional (say) finite element approximation
— are often quite modest.
13
Our work
6, 8, 9, 14, 15, 20
differs from these earlier efforts in several important
ways: first, we develop global approximation spaces;
second, we introduce rigorous a posteriori error esti-
mators; and third, we exploit off-line/on-line compu-
tational decompositions (see
2
for an earlier application
of this strategy.) These three ingredients allow us —
for the restricted but important class of “parameter-
affine” problems — to reliably decouple the generation
and projection stages of reduced-basis approximation,
thereby effecting computational economies of several
orders of magnitude.
In this paper we develop new a posteriori error esti-
mation procedures for noncoercive linear, and certain
nonlinear, problems that — unlike our earlier “asymp-
totic” techniques
8, 15
— yield rigorous error statements
for all N. We consider three particular examples: the
Helmholtz (reduced-wave) equation (Section 2); a cu-
bically nonlinear Poisson equation (Section 3); and
Burgers equation (Section 4) — a model for incom-
pressible Navier-Stokes. The Helmholtz (and Burgers)
example introduce our new lower bound constructions
for the requisite inf-sup (singular value) stability fac-
tor; the cubic nonlinearity exercises symmetry factor-
ization procedures necessary for treatment of high-
order Galerkin summations in the (say) residual dual-
norm calculation; and the Burgers equation illustrates
our accommodation of potentially multiple solution
branches in our a posteriori error statement. Numer-
ical results are presented that demonstrate the rigor,
sharpness, and efficiency of our proposed error bounds,
and the application of these bounds to adaptive (opti-
mal) approximation.
2 Noncoercive Linear Problems:
Helmholtz Equation
2.1 Preliminaries
We consider a suitably regular domain Ω ⊂ R
d
,
1 ≤ d ≤ 3, with boundary ∂Ω. We then intro-
duce a Hilbert space Y with associated inner product,
( · , · )
Y
, and induced norm, k · k
Y
. We shall assume
that H
1
0
(Ω) ⊂ Y ⊂ H
1
(Ω), where H
1
(Ω) ≡ {v ∈
L
2
(Ω), ∇v ∈ (L
2
(Ω))
d
}, H
1
0
≡ {v ∈ H
1
(Ω)|v|
∂Ω
= 0},
and L
2
(Ω) is the space of square-integrable functions
over Ω. We shall further assume that
( ·, · )
Y
= ( ·, · )
H
1
(Ω)
,
k ·k
Y
= k ·k
H
1
(Ω)
,
(1)
where
(w, v)
H
1
(Ω)
≡
Z
Ω
∇w · ∇v + wv, ∀ w, v ∈ H
1
(Ω) ,
kvk
H
1
(Ω)
≡
Z
Ω
|∇v|
2
+ v
2
, ∀v ∈ H
1
(Ω) .
(2)
More general inner products and norms can (and
should) be considered, as discussed in Section 2.4.2.
We shall denote by Y
0
the dual space of Y . For a
g ∈ Y
0
, the dual norm is given by
kgk
Y
0
= sup
v ∈Y
g(v)
kvk
Y
. (3)
If we introduce the “representation” operator Y: Y
0
→
Y such that, for any g ∈ Y
0
,
(Yg, v)
Y
= g(v) , (4)
then
kgk
Y
0
= kYgk
Y
; (5)
this is simply a statement of the Riesz representation
theorem.
We now introduce our parametrized bilinear form.
We first define a parameter set D
µ
⊂ R
P
, a typical
point in which — our input P -tuple — shall be denoted
µ; we can then define, for any µ ∈ D
µ
, our bilinear
form a( · , · ; µ): Y × Y → R. We shall assume that
a satisfies a continuity and inf-sup condition for all
µ ∈ D, as we now state more precisely.
It shall prove convenient to state our hypotheses in
terms of a “supremizing” op e rator T
µ
: Y → Y . In
particular, for any given µ ∈ D
µ
, and any w ∈ Y ,
(T
µ
w, v)
Y
= a(w, v; µ), ∀ v ∈ Y ; (6)
it is readily shown that
T
µ
w = arg sup
v ∈Y
a(w, v; µ)
kvk
Y
. (7)
Furthermore, if we define the inf-sup (singular value)
and continuity c onstants as
β(µ) ≡ inf
w∈Y
sup
v ∈Y
a(w, v; µ)
kwk
Y
kvk
Y
(8)
and
γ(µ) ≡ sup
w∈Y
sup
v ∈Y
a(w, v; µ)
kwk
Y
kvk
Y
, (9)
then,
β(µ) = inf
w∈Y
σ(w; µ) , (10)
γ(µ) = sup
w∈Y
σ(w; µ) , (11)
where
σ(w; µ) ≡
kT
µ
wk
Y
kwk
Y
. (12)
2 of 18
American Institute of Aeronautics and Astronautics Paper 2003-3847

Our assumptions are then: for some positive constant
ε
s
, ε
s
≤ β(µ) ≤ γ(µ) < ∞, ∀ µ ∈ D
µ
.
We next define the bilinear form b(·, ·; µ): Y ×Y →
R as
b(w, v; µ) = (T
µ
w, T
µ
v)
Y
, ∀w, v ∈ Y . (13)
We then introduce the eigenproblem: Given µ ∈ D
µ
,
find χ
i
(µ) ∈ Y, λ
i
(µ) ∈ R, i = 1, . . . , ∞, such that
b(χ
i
(µ), v; µ) = λ
i
(µ)(χ
i
(µ), v)
Y
, ∀ v ∈ Y , (14)
kχ
i
(µ)k
Y
= 1 . (15)
We shall, for convenience, assume that the spectrum
is discrete (in actual practice we require only that the
first few modes belong to the discrete component). In
that case, we may assume that
b(χ
i
(µ), χ
j
(µ); µ) = λ
i
(µ)(χ
i
(µ), χ
j
(µ))
Y
= λ
i
(µ)δ
ij
,
(16)
where δ
ij
is the Kronecker-delta symbol; that 0 <
λ
1
(µ) ≤ λ
2
(µ) ≤ ···; and that Y = span {χ
i
(µ), i =
1, . . . , ∞}. Note that, from (10)-(14), β(µ) =
p
λ
1
(µ);
furthermore, γ(µ) is an upper bound for the spectrum.
We shall make the further assumption that a is
“affine in the parameter” in the sense that, for some
finite Q,
a(w, v; µ) =
Q
X
q=1
Θ
q
(µ) a
q
(w, v) , (17)
where Θ: D
µ
→ R
Q
are differentiable parameter-
dependent coefficient functions, and the a
q
: Y × Y →
R, 1 ≤ q ≤ Q, are parameter-independent bilinear
forms. We define, for future reference,
D
qp
= max
µ∈D
µ
∂Θ
q
∂µ
p
(µ)
, (18)
for 1 ≤ q ≤ Q, 1 ≤ p ≤ P . Furthermore, we as sume
that the a
q
are continuous in the sense that there exist
positive finite constants Γ
q
, 1 ≤ q ≤ Q, such that
|a
q
(w, v)| ≤ Γ
q
|w|
q
|v|
q
; (19)
here | ·|
q
: H
1
(Ω) → R are seminorms that satisfy
Q
X
q=1
|v|
2
q
!
1/2
≤ C
1/2
Y
kvk
Y
, ∀v ∈ Y , (20)
where C
Y
is a finite constant.
Finally, it directly follows from (6) and (17) that,
for any w ∈ Y , T
µ
w ∈ Y may be expressed as
T
µ
w =
Q
X
q=1
Θ
q
(µ) T
q
w , (21)
where, for any w ∈ Y , T
q
w, 1 ≤ q ≤ Q, is given by
(T
q
w, v)
Y
= a
q
(w, v), ∀ v ∈ Y . (22)
Note that the operators T
q
: Y → Y are independent
of the parameter µ.
2.2 Problem Formulation
2.2.1 Weak Statement
We introduce an output functional ` ∈ Y
0
and
“data” functional f ∈ Y
0
. Our weak statement of the
partial differential equation is then: Given µ ∈ D
µ
,
find
s = `(u(µ)) , (23)
where u(µ) ∈ Y satisfies
a(u(µ), v; µ) = f(v), ∀v ∈ Y . (24)
In the language of the introduction, s(µ) is our output,
and u(µ) is our field variable.
In actual practice, we shall replace (23)–(24) with a
truth approximation: Given µ ∈ D
µ
, find
s
N
(µ) = `(u
N
(µ)) ,
where u
N
(µ) ∈ Y
N
⊂ Y satisfies
a(u
N
(µ), v; µ) = f(v), ∀v ∈ Y
N
, (25)
and Y
N
is a finite element approximation subspace.
We assume that N is chosen sufficiently large that
s
N
(µ) and u
N
(µ) may be effectively equated with
s(µ) and u(µ), respectively. We shall thus distinguish
between Y
N
and Y only in our discussion of compu-
tational complexity. (Note that issues associated with
a possible continuous component to the spectrum of
(14) may be addressed by considering Y as the limit
of Y
N
, N → ∞.)
2.2.2 Reduced-Basis Approximation
The focus of the current paper is a posteriori error
estimation. We shall thus take our reduced-basis ap-
proximation as given. In particular, we assume that
we are provided with a reduced-basis approximation
to u(µ), u
N
(µ) ∈ W
N
, where
W
N
= span {ζ
n
≡ u(µ
n
), 1 ≤ n ≤ N} , (26)
S
N
= {µ
1
∈ D
µ
, . . . , µ
N
∈ D
µ
}, and u(µ
n
) satisfies
(24) (in practice, (25)) for µ = µ
n
. It follows that
u
N
(µ) may be expressed as
u
N
(µ) =
N
X
n=1
u
Nn
(µ) ζ
n
. (27)
The reduced-basis approximation to the output s(µ),
s
N
(µ), is given by s
N
(µ) = `(u
N
(µ)).
For the purposes of this paper, we shall consider only
standard Galerkin projections: a(u
N
(µ), v; µ) = f(v ),
∀ v ∈ W
N
. Howe ver, the discrete inf-sup param-
eter associated with the latter may not be “good,”
with corresponding detriment to the accuracy of u
N
(µ)
and hence s
N
(µ). More s ophisticated minimum-
residual
8, 18
and in particular Petrov-Galerkin
7, 18
ap-
proaches restore (guaranteed) stability, albeit at some
additional c omplexity and cost.
3 of 18
American Institute of Aeronautics and Astronautics Paper 2003-3847

2.2.3 Error Estimation: Objective
We now wish to develop a posteriori error bounds
∆
N
(µ) and ∆
s
N
(µ) such that
ke(µ)k
H
1
(Ω)
≤ ∆
N
(µ) , (28)
and
|s(µ) −s
N
(µ)| = |`(e(µ))| ≤ ∆
s
N
(µ) , (29)
where e(µ) ≡ u(µ) − u
N
(µ). For the purposes
of this paper, we shall focus on the H
1
(Ω) bound,
∆
N
(µ), in terms of which ∆
s
N
(µ) can be expressed as
kY`k
Y
∆
N
(µ); the latter may be significantly improved
by the introduction of adjoint techniques.
5, 15
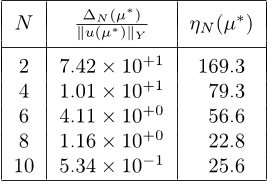
It shall prove convenient to introduce the notion of
effectivity, defined (here) as
η
N
(µ) ≡
∆
N
(µ)
ke(µ)k
H
1
(Ω)
. (30)
Our certainty requirement (28) may be stated as
η
N
(µ) ≥ 1, ∀ µ ∈ D
µ
. However, for efficiency, we
must also require η
N
(µ) ≤ C
η
, where C
η
≥ 1 is a con-
stant independent of N and µ; preferably, C
η
is close to
unity, thus ensuring that we cho os e the smallest N —
and hence most economical — reduced-basis approxi-
mation consistent with the specified error tolerance.
2.3 A Posteriori Error Estimation
2.3.1 Error Bound
We assume that we are given a
ˆ
β(µ) such that, for
the given inner product ( ·, ·)
Y
≡ (·, ·)
H
1
(Ω)
(which in
our previous papers
14, 2 0
would be denoted a “bound
conditioner”),
β(µ) ≥
ˆ
β(µ) ≥ (1 − τ) ε
s
, ∀µ ∈ D
µ
, (31)
where τ ∈ ]0, 1[ . We then define our error bound as
∆
N
(µ) ≡
kYr( · ; µ)k
Y
ˆ
β(µ)
, (32)
where
r(v; µ) = f(v) − a(u
N
(µ), v; µ), ∀ v ∈ Y , (33)
is the residual associated with u
N
(µ). Note it follows
from (24) that (33) may be restated as
a(e(µ), v; µ) = r(v; µ), ∀ v ∈ Y , (34)
where we recall that e(µ) ≡ u(µ) −u
N
(µ).
We can then state
Proposition 1 For the error bound ∆
N
(µ) of (32),
the effectivity satisfies
1 ≤ η
N
(µ) ≤
γ(µ)
(1 −τ ) ε
s
, ∀ µ ∈ D , (35)
for all N ∈ N.
Proof It follows from (4), (6), and (34) that
kYr( · ; µ)k
Y
= kT
µ
e(µ)k
Y
. (36)
Furthermore, from (12) we know that
ke(µ)k
Y
=
kT
µ
e(µ)k
Y
σ(e(µ); µ)
, (37)
and hence from (1), (30), (32), (36), and (37)
η
N
(µ) =
σ(e(µ); µ)
ˆ
β(µ)
. (38)
The result then directly follows from (10), (11), (31),
and (38).
We note that our proof (or bound) does not exploit
any special properties of e(µ) (or u
N
(µ)).
It remains to develop our lower bound construc-
tion,
ˆ
β(µ), and to demonstrate that both
ˆ
β(µ) and
kYr( · ; µ)k
Y
may be computed efficiently (that is, in
complexity independent of N).
2.3.2 Inf-Sup Lower Bound Construction
Many of the most obvious eigenvalue approximation
concepts are not relevant here, since we require a lower,
not upper, bound. We thus develop a construction
particularly s uited to our context.
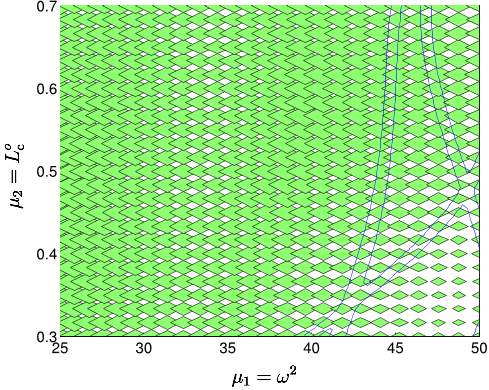
We assume that we are given a set of J parameter
points, L
J
≡ {µ
1
∈ D
µ
, . . . , µ
J
∈ D
µ
}, and associated
set of polygonal regions R
µ
j
,τ
, 1 ≤ j ≤ J, where
R
µ,τ
≡ {µ ∈ D
µ
|B
µ
q
(µ) ≤
τ
C
Y
β(µ), 1 ≤ q ≤ Q} ,
(39)
and
B
µ
q
(µ) = Γ
q
P
X
p=1
D
qp
|µ
p
− µ
p
| ; (40)
we further ass ume that
J
[
j=1
R
µ
j
,τ
= D
µ
. (41)
We then define J : D
µ
→ {1, . . . , J} such that, for a
given µ, R
µ
J (µ)
,τ
is that region (or a selected region)
which contains µ.
Our lower bound is then: Given µ ∈ D
µ
,
ˆ
β(µ) = β(µ
J (µ)
) −C
Y
B
µ
J (µ)
max
(µ) , (42)
where
B
µ
max
(µ) = max
q∈{1 ,. ..,Q}
B
µ
q
(µ) (43)
for B
µ
q
(µ) defined in (40).
We can now state
Proposition 2 The construction
ˆ
β(µ) of (42) satis-
fies the inequality (31).
4 of 18
American Institute of Aeronautics and Astronautics Paper 2003-3847