
“© 2013 IEEE. Personal use of this material is permitted. Permission from IEEE must be
obtained for all other uses, in any current or future media, including
reprinting/republishing this material for advertising or promotional purposes, creating
new collective works, for resale or redistribution to servers or lists, or reuse of any
copyrighted component of this work in other works.”


method and assumptions and in section IV and V respectively
performance metrics and result are presented. Finally in section
VI, conclusion and possible future work are presented.
II. RELATED WORK
A large proportion of relocation and movement algorithms
in the literature [3], [6], [7], [8], [9], [10], [11], [12], [13],
[14], [15] are devoted to currently deployed nodes in or-
der to give the network more flexibility, swiftness to react
autonomously in the environments where centralized control
and supervision are not feasible. Each of these algorithms
are aimed at different and overlapping goals such as network
connectivity [13], lifetime [12], re-alignment of unbalanced
deployments [7], coverage increase [7], recovery of small
and large scale coverage holes [6], [9], [14]. However, these
algorithms more or less would be able achieve other than their
primary objectives. Thus, the performance and efficacy of these
algorithms should also be investigated for applications other
than their primary design goals. As most algorithms partially
inspired and evolved from each other, it is hard to draw fine
line between them. They can be mainly classified into virtual
force-based (radial [7], [16] or angular [13]), voronoi-based
[14] and flip-based [6] movement algorithms. Among these
algorithms in WSNs, the amount of unnecessary movements,
oscillations and power exhaustion of nodes with local interac-
tions in the distributed relocation algorithms especially with a
harsh and hostile environments with lack of central supervision
and operation should be reduced as possible. In order to
save nodes’ power and to localize movement to a specific
area in the network, relocation algorithm can be applied to
a selected set of nodes [17], [18], fully or partially to avoid
unnecessary node oscillations or energy consumption caused
by careless movement strategies. Reduction in overhead and
delay of centralized relocation paradigm comes at the price
of increased uncertainty among autonomous nodes who have
local interactions within their ranges.
Although fuzzy logic relocation model shown to be candi-
date solution to address such a uncertainty for the autonomous
moving nodes [10], among indefinite choices, proper and
justifiable fuzzy parameters and membership functions should
be selected. In proposed model, the proper fuzzy parameters
in fuzzy logic relocation model can be obtained by applying
PSO technique locally with different ranges and globally over
the given deployed area. similar to [10] with different angular,
boundary conditions and movement strategies, the efficiency
and performance of the given model in terms of coverage,
uniformity and movement are also compared with distributed
Self-Spreading Algorithm (DSSA) [7] which benefited from
expected global node density.
III. M
ETHODS AND ASSUMPTIONS
With the given sensing range R
s
and transmission range
R
c
, sensor nodes are modeled as unite disk graphs (UDG)
and are bi-directionally connected when they reside within
their one another’s ranges. Nodes are randomly deployed in
2D rectangular field of [x
min
x
max
] × [y
min
y
max
] with the
uniform distribution. Nodes’ locations are known by either
centralized or distributed localization algorithms [19], [20].
Circular zone around the node is defined as a circle with radius
of R
zone
(R
zone
= k · R
c
) with the node in the center of
circle and are used to obtain the fuzzy parameters from nodes’
neighbours residing in the given zone via PSO.
TABLE I: Fuzzy Rules [10]
(a) Pair Radial Force
System
Distance Pressure
Very Far No Action(0)
Far Pull hard(-1)
Moderate Pull(-0.5)
Close Push(0.5)
Too Close Push Hard(1)
(b) Pair Angular Force Sys-
tem
Distance Pressure
Very Far Hard(1)
Far Medium(0.75)
Moderate Slow(0.5)
Close Very Slow(0.25)
Too Close Nothing (0)
TABLE II: Membership Functions
z-function
f
z
(x; a, b) =
1, x ≤ a
1 − 2
x−a
b−a
2
, a ≤ x ≤
a+b
2
2
x−b
b−a
2
,
a+b
2
≤ x ≤ b
0, x ≥ b
Symmetric Gaussian function
f
g
(x; σ, µ) = e
−(x−µ)
2
2σ
2
s-function
f
s
(x; c, d) =
0, x ≤ c
2
x−c
d−c
2
, c ≤ x ≤
c+d
2
1 − 2
x−d
d−c
2
,
c+d
2
≤ x ≤ d
1, x ≥ d
A. Fuzzy Logic Parameters
Fuzzy rule-based systems are applied in a variety of
research areas [21], [22]. For fuzzy control problems Takagi-
Sugeno (TS) [21] rule based systems briefly are described as
follows:
Rule R
j
: if x
1
is A
j1
and · · · and x
n
is A
jn
then y
j
= a
0j
+ a
1j
x
1
+ · · · + a
nj
x
n
(1)
where x = (x
1
, x
2
, ..., x
n
) is an n-dimensional input, A
nj
is
a fuzzy membership and y is a non-fuzzy output. Fuzzy rule
base system’s output is calculated from the following equation,
y =
p
j=1
µ
j
(x) · y
j
N
j=1
µ
j
(x)
, (2)
µ
j
(x) = µ
1j
(x) ⊗ µ
2j
(x) ⊗ · · · ⊗ µ
nj
(x) (3)
p is the total number of rules. Similar to [10] two different
fuzzy inference systems are used: fuzzy radial pair force
and fuzzy angular force. Both fuzzy radial pair force system
and fuzzy angular force system have one input as distance
with 3 gaussian functions, one z-function and one s-function
memberships (Table II) and one crisp output, pressure which
can take the fuzzy values push hard, push, no action, pull
and pull hard. The rules of these systems are listed in Table
I. Membership function parameters a, b, c, d, µ, σ computed
using particle swarm optimization. Figure 1 is brought as the
example of respectively tuned radial and angular membership
functions for angular strategy A
1
, boundary condition B
2
and
movement strategy F RAM. Hence, fuzzy parameters can be
tuned using particle swarm optimization with regard to linear
weighted combinations of metrics in terms of percentage of
coverage, uniformity, and average movement equation 4.
F
∗
= argmax
F
{w
1
· C(F ) − w
2
· U (F ) − w
3
· M (F )} (4)
w
1
, w
2
, w
3
are respectively weights for coverage (C), unifor-
mity (U), and average movement (M ). F is a set of fuzzy
parameters tuned by PSO with regard to the performance
weights. Thus, parameters can be tuned based on one or linear
combination of the metrics. The negative and positive signs

0 5 10 15
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Radial Distance(m)
Angular Strategy=1, Boundary Condition= 2, Movement Algs.= FARM, Rzone: 1Rc
Too Close
Close
Moderate
Far
Very Far
(a) Radial Membership
0 50 100 150 200 250 300 350
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Angle(degree)
Angular Strategy= 1, Boundary Conditions= 2, Movement Algs.= FRAM, Rzone= 1Rc
Too Close
Close
Moderate
Far
Very Far
(b) Angular Membership
Fig. 1: Radial and Angular Membership function
used where performance metrics should be minimized (i.e.
movement, uniformity) or maximized (i.e. coverage) respec-
tively. In order to tune parameters PSO is applied in two
different global and local zone range which are as follows:
In global range, PSO applied on all deployed nodes over
whole 2D rectangular field ([x
min
x
max
]×[y
min
y
max
]) while
in local zone-range, proportion of nodes N
sel
from set of
deployed nodes N
total
(N
sel
≤ N
total
) are randomly selected
with uniform distribution. PSO is applied for each selected
node with a zone-range of R
zone
(R
zone
= k · R
c
) around
selected node by taking account node’s neighbours residing
within its R
zone
range. It should be noted that in both local and
global ranges, boundary conditions are considered in tuning
fuzzy parameters.
B. PSO structures
In this paper, the constriction coefficient PSO used similar
to the [23]. Thus,in this approach the velocity update equation
is as follows:
υ
ij(t+1)
= χ
υ
ij(t)
+ φ
1
y
ij(t)
− x
ij(t)
+ φ
2
ˆy
ij(t)
− x
ij(t)
(5)
y
ij
is the particle best and ˆy
ij
is the global best particles and,
χ =
2k
2 − φ −
φ(φ − 4)
(6)
with φ = φ
1
+ φ
2
, φ
i
= c
i
r
i
i = 1, 2. Equation 6 is
used under the constraint that φ ≥ 4 and k, r
i
∈ [0, 1]. The
parameter k in the equation 6 controls the exploration and
exploitation. For k ∼ 0, fast convergence is expected and for
k ∼ 1 we can expect slow convergence with high degree of
exploration [23]. Each particle consists of two arrays, which
one is related to the memberships of the pair force fuzzy
systems and another one is related to the memberships of
the angular force fuzzy systems. Each fuzzy system has 5
memberships and each membership is specified by its mean
and variance, therefore each array has 10 cells.
C. Boundary Strategies
In relocation algorithm, behaviour of moving nodes while
approaching to the given area’s boundaries (i.e. [x
min
, x
max
]×
Iteration i
Iteration i+1
Angular Force
Radial Force
Fig. 2: Fuzzy Node Movement Algorithms [10]
[y
min
, y
max
]) with respect to different boundary conditions
should be taken into account. Boundary strategies applied
in [10] are adopted here which are non-stop at boundary,
stop at boundary, wrap around. (B
1
)-In non-stop at boundary,
regardless of boundaries of given area, nodes relocate towards
their new locations without limit. (B
2
)-In stop at boundary,
nodes stop at boundaries of given area and their movements
are limited if their new computed locations are beyond the
area boundaries. (B
3
)-In wrap around, according to toroidal
surface, nodes are wrapped around to other (opposite) sides if
new computed locations go beyond the area boundaries.
D. Angular Force Strategies
Force exerting node n
fv
is considered as vertex of angle
α = (n
1
, n
fv
, n
2
) (0 < α ≤ 180
◦
) with each pair of
its neighbours n
1
,n
2
. Angular force strategies in [10] based
on exerted forces from node’s neighbours can be considered
as:(A
1
)-Smallest Angular Movement Strategy, among exerted
angular forces from node’s neighbours, the one is selected
that causes smallest node angular movement. (A
2
)-Closest
Neighbour Movement Strategy, among exerted angular forces
from nodes’ neighbours, the closest neighbour is selected as
the exerting angular nodes.
E. Fuzzy Node Movement Algorithms
In our model, similar to [10], fuzzy node movement
algorithms are as: Fuzzy radial movement (FRM)- Nodes are
mutually affected by radial force from their neighbours. The
amount of node movement is related to overall push/pull virtual
forces from their in-range neighbours. Fuzzy angular Move-
ment (FAM)- Nodes exert a force to their in-range neighbours
depending on aforementioned angular force strategies. FRM
then FAM (FRAM)- FAM is applied to result of FRM in
consecutive iterations. (Figure 2). FAM then FRM (FARM)-
FRM is applied to the result of FAM in consecutive iterations
(Figure 2).
IV. P
ERFORMANCE METRICS
The performance metrics presented are: Percentage
of Coverage(C)-Suppose that a 2-D rectangular area of
[x
min
, x
max
] × [y
min
, y
max
] is divided into grid cells. The
coverage of the given grid cells is defined as the number
of nodes covering the cells’ corner coordinates z
i
=(x
i
, y
i
).
Thus, percentage of 1-coverage is defined as the ratio of
grid cells within range of at least one sensor node to the
total number of area’s grid cells. This metric illustrates how
an efficient relocation algorithms are able to cover the given
area. Uniformity (U )-The measure of nodes being uniformly

0 50 100 150 200 250 300 350 400 450 500
80
81
82
83
84
85
86
87
88
89
90
Number of Iterations
Percentage of 1−Coverage(100%)
# Experiments = 500, Boundary Condition = 2, Angular Strategy = 1
Movement Algorithm = FRM , [ω
1
ω
2
ω
3
] = [0 0 1]
DSSA
Global
R
zone
= 1R
c
R
zone
= 2R
c
R
zone
= 4R
c
(a) Percentage of 1-Coverage,(A
1
,B
2
,FRM)
0 50 100 150 200 250 300 350 400 450 500
10
−15
10
−10
10
−5
10
0
Number of Iterations
Uniformity
# Experiments = 500, Boundary Condition = 2, Angular Strategy = 1
Movement Algorithm = FRM , [ω
1
ω
2
ω
3
] = [0 0 1]
DSSA
Global
R
zone
= 1R
c
R
zone
= 2R
c
R
zone
= 4R
c
(b) Uniformity,(A
1
,B
2
,FRM)
0 50 100 150 200 250 300 350 400 450 500
10
−15
10
−10
10
−5
10
0
Number of Iterations
Average Movement(m)
# Experiments = 500, Boundary Condition = 2, Angular Strategy = 1
Movement Algorithm = FRM , [ω
1
ω
2
ω
3
] = [0 0 1]
DSSA
Global
R
zone
= 1R
c
R
zone
= 2R
c
R
zone
= 4R
c
(c) Average Movement,(A
1
,B
2
,FRM)
Fig. 3: Performance Comparison of Relocation Algorithm for
globally and locally (R
zone
={1,2,4}·R
c
) Tuned fuzzy param-
eters
distributed is defined in [7]. U is defined as the average local
standard deviation of internodal distances [7].
U
i
=
k
i
j=1
(D
i,j
− M
i
)
2
k
i
1/2
, U =
N
i=1
U
i
N
, (7)
where N is the total number of nodes, k
i
is number of
neighbours of the ith node, D
i,j
is the distance between the ith
and jth nodes, and M
i
is the mean internodal distance between
the ith node and its neighbours [7]. Average Movement (M )
- It is defined as total movement of nodes in each iteration
over the number of nodes in the given iteration. As movement
is related to amount of node’s consumed energy, average
0 50 100 150 200 250 300 350 400 450 500
80
82
84
86
88
90
92
Number of Iterations
Percentage of 1−Coverage(100%)
# Experiments = 500, Boundary Condition = 2, Angular Strategy = 1
R
zone
= 1R
c
, [ω
1
ω
2
ω
3
] = [0 0 1]
DSSA
FRM
FAM
FRAM
FARM
(a) Percentage of 1-Coverage
0 50 100 150 200 250 300 350 400 450 500
10
−15
10
−10
10
−5
10
0
Number of Iterations
Uniformity
# Experiments = 500, Boundary Condition = 2, Angular Strategy = 1
R
zone
= 1R
c
, [ω
1
ω
2
ω
3
] = [0 0 1]
DSSA
FRM
FAM
FRAM
FARM
(b) Uniformity
0 50 100 150 200 250 300 350 400 450 500
10
−15
10
−10
10
−5
10
0
Number of Iterations
Average Movement(m)
# Experiments = 500, Boundary Condition = 2, Angular Strategy = 1
R
zone
= 1R
c
, [ω
1
ω
2
ω
3
] = [0 0 1]
DSSA
FRM
FAM
FRAM
FARM
(c) Average Movement
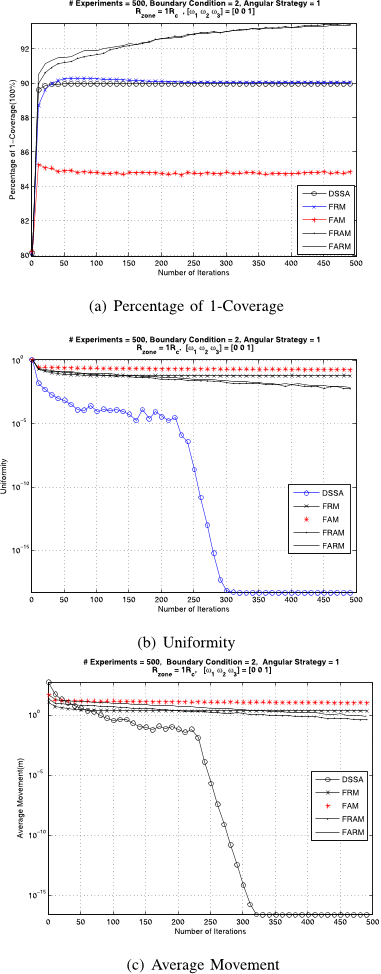
Fig. 4: Performance of Different Movement Strategies with
Boundary condition B
2
and Angular Force Strategy A
1
movement of nodes in each iteration represent a suitable metric
for comparison of various node relocation algorithms in the
context of energy efficiency.
V. RESULTS
The proposed node relocation algorithm was simulated
by Matlab and N =100 nodes with the transmission and
sensing range of R
c
=R
s
=15 are distributed uniformly in
the rectangular 2-D space of [−100 100] × [−100 100]m
2
.
The fuzzy parameters are obtained locally as N
sel
= 30 of
total deployed nodes N
tot
= 100 are randomly selected with
zone ranges of R
zone
=(1, 2, 4)·R
c
. The fuzzy parameters are
tuned via particle swarm optimization (k = 0.5, c
1
= 3,
c
2
= 3 equation 6) with boundary conditions of B
1
, B
2
,
B
3
and angular strategies of A
1
and A
2
. The membership
parameters are also obtained globally in rectangular field of

![TABLE I: Fuzzy Rules [10]](/figures/table-i-fuzzy-rules-10-fg7rtkq3.png)


![Fig. 2: Fuzzy Node Movement Algorithms [10]](/figures/fig-2-fuzzy-node-movement-algorithms-10-392czm8g.png)