The Astrophysical Journal, 754:36 (17pp), 2012 July 20 doi:10.1088/0004-637X/754/1/36
C
2012. The American Astronomical Society. All rights reserved. Printed in the U.S.A.
ACCURATE SIMULATIONS OF BINARY BLACK HOLE MERGERS IN FORCE-FREE ELECTRODYNAMICS
Daniela Alic
1
, Philipp Moesta
1,2
, Luciano Rezzolla
1,3
, Olindo Zanotti
4
,andJos
´
e Luis Jaramillo
1
1
Max-Planck-Institut f
¨
ur Gravitationsphysik, Albert-Einstein-Institut, Potsdam, Germany
2
TAPIR, MC 350-17, California Institute of Technology, Pasadena, CA 91125, USA
3
Department of Physics and Astronomy, Louisiana State University, Baton Rouge, LA, USA
4
Laboratory of Applied Mathematics, University of Trento, Via Mesiano 77, 38123 Trento, Italy
Received 2012 April 7; accepted 2012 May 9; published 2012 July 3
ABSTRACT
We provide additional information on our recent study of the electromagnetic emission produced during the inspiral
and merger of supermassive black holes when these are immersed in a force-free plasma threaded by a uniform
magnetic field. As anticipated in a recent letter, our results show that although a dual-jet structure is present, the
associated luminosity is ∼100 times smaller than the total one, which is predominantly quadrupolar. Here we discuss
the details of our implementation of the equations in which the force-free condition is not implemented at a discrete
level, but rather obtained via a damping scheme which drives the solution to satisfy the correct condition. We show
that this is important for a correct and accurate description of the current sheets that can develop in the course of the
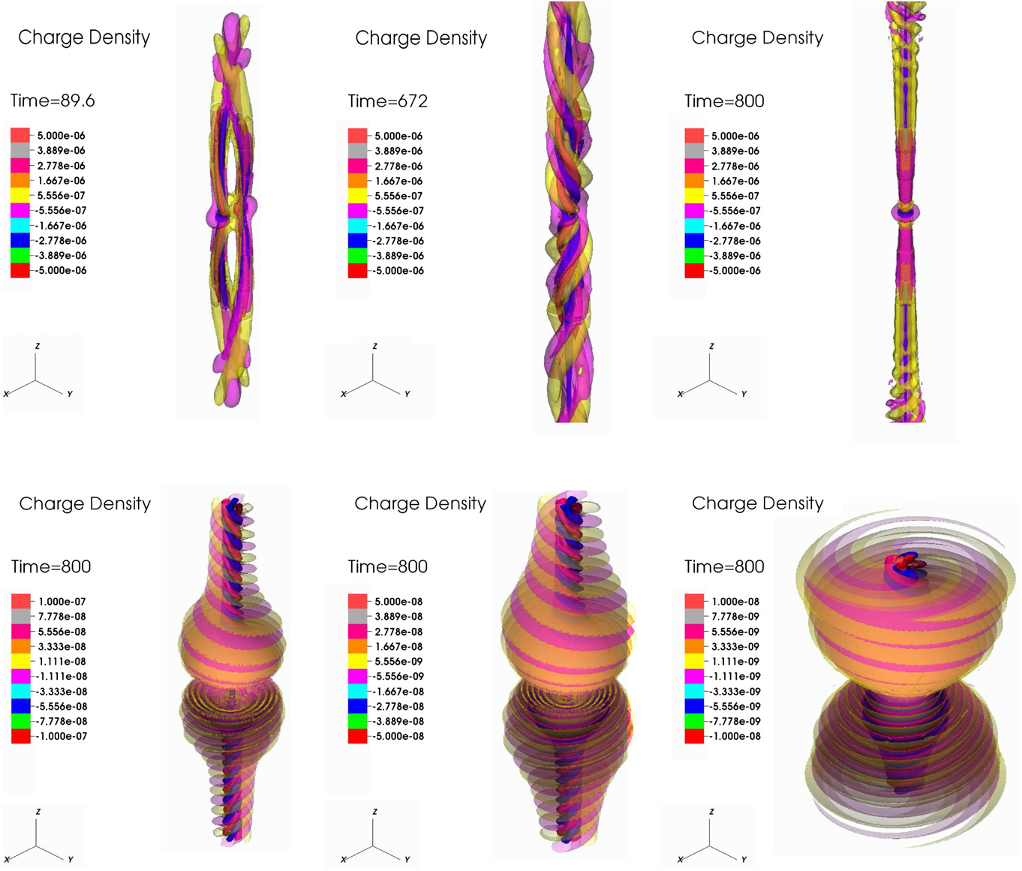
simulation. We also study in greater detail the three-dimensional charge distribution produced as a consequence of
the inspiral and show that during the inspiral it possesses a complex but ordered structure which traces the motion
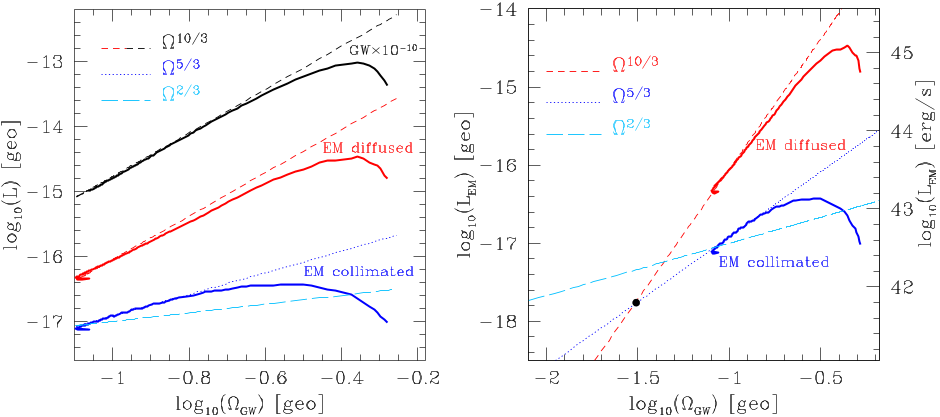
of the two black holes. Finally, we provide quantitative estimates of the scaling of the electromagnetic emission
with frequency, with the diffused part having a dependence that is the same as the gravitational-wave one and that
scales as L
non-coll
EM
≈ Ω
10/3−8/3
, while the collimated one scales as L
coll
EM
≈ Ω
5/3−6/3
, thus with a steeper dependence
than previously estimated. We discuss the impact of these results on the potential detectability of dual jets from
supermassive black holes and the steps necessary for more accurate estimates.
Key words: binaries: close – galaxies: jets – gravitation – magnetic fields – plasmas – relativistic processes
Online-only material: color figures
1. INTRODUCTION
The gravitational interaction among galaxies, most of which
are supposed to host a supermassive black hole (BH), with
M 10
6
M
(Shankar et al. 2004; Lou & Jiang 2008), is a
well-established observational fact (Gopal-Krishna et al. 2003;
Ellison et al. 2011; Mohamed & Reshetnikov 2011; Lambas
et al. 2012). Moreover, in a few documented astrophysical cases,
strong indications exist to believe that a binary merger among
supermassive BHs has occurred or is ongoing (Rodriguez et al.
2006; Komossa et al. 2003; Dotti et al. 2009).
A strong motivation for studying supermassive binary black
holes (SMBBHs) comes from the fact that their gravitational sig-
nal will be detected by the planned Laser Interferometric Space
Antenna (eLISA/NGO; Amaro-Seoane et al. 2012;Bin
´
etruy
et al. 2012). When combined with the usual electromagnetic
(EM) emission, the detection of gravitational waves (GW) from
these systems will provide a new tool for testing a number of fun-
damental astrophysical issues (Cornish & Porter 2007;Haiman
et al. 2009; Phinney 2009). For this reason, SMBBHs are cur-
rently attracting widespread interest, both from an observational
and a theoretical point of view (Rezzolla 2009; Reisswig et al.
2009; Kesden et al. 2010; Kocsis et al. 2011; Tanaka et al. 2012;
Sesana et al. 2012; Barausse 2012). According to the simplest
picture that has gradually emerged through a series of semi-
analytical studies and numerical simulations (Milosavlje
´
c&
Phinney 2005; MacFadyen & Milosavljevi
´
c 2008; Roedig et al.
2011; Bode et al. 2012), the accretion disk formed around the
two merging BHs, commonly referred to as the “circumbinary”
accretion disk, can follow the dynamical evolution of the system
up until the dynamical timescale for the emission of GWs, which
scales like ∼D
4
, where D is the separation of the binary, be-
comes shorter than the viscous timescale, which instead scales
like ∼D
2
. When this happens, the circumbinary accretion disk is
essentially decoupled from the binary, which rapidly enters the
final stages of the inspiral. Under these conditions, neglecting
the inertia of the accreting fluid can be regarded as a very good
approximation. In contrast, magnetic fields generated by the cir-
cumbinary accretion disk could play an important role and the
dynamics of the plasma in the inner region can then be described
within the force-free (FF) approximation. These physical con-
ditions are indeed similar to those considered in the seminal
investigations of BH electrodynamics of Blandford and Zna-
jek (Blandford & Znajek 1977), who addressed the question of
whether the rotational energy of an isolated BH can be extracted
efficiently by a magnetic field. After the first two-dimensional
investigations of Komissarov and Barkov (Komissarov 2004;
Komissarov & Barkov 2009), the numerical study of BH mag-
netospheres has now entered a mature phase in the context of
SMBBHs evolution.
In an extensive analysis, but still in the absence of currents
and charges, i.e., in electrovacuum, M
¨
osta et al. (2010)showed
that, even though the EM radiation in the lowest = 2 and
m = 2 multipole reflects the gravitational one, the energy
emitted in EM waves is ∼13 orders of magnitude smaller than
that emitted in GWs for a reference binary with mass M =
10
8
M
and a magnetic field B = 10
4
G, thus casting serious
doubts about a direct detection of the two different signals.
However, a series of more recent numerical simulations in which
currents and charges are taken into account have suggested the
intriguing possibility that a mechanism similar to the original
one proposed by Blandford and Znajek may be activated in the
case of binaries (Palenzuela et al. 2009a, 2010a, 2010b, 2010c;
Moesta et al. 2012; note that Palenzuela et al. 2010a, 2010b;
1

The Astrophysical Journal, 754:36 (17pp), 2012 July 20 Alic et al.
Moesta et al. 2012 also make use of an FF approximation).
In particular, the Blandford–Znajek mechanism is likely to be
valid under rather general conditions, namely even if stationarity
and axisymmetry are relaxed and even if a non-spinning BH is
simply boosted through a uniform magnetic field. Moreover,
for such uniform magnetic field, the emitted EM flux shows a
high degree of collimation, making the EM counterpart more
easily detectable. A less optimistic view has emerged recently
in Moesta et al. (2012, hereafter Paper I), where we have shown,
through independent calculations in which the EM emission
was extracted at much larger radii, that the dual-jet structure
is indeed present but energetically subdominant with respect to
the non-collimated and predominantly quadrupolar emission. In
particular, even if the total luminosity at merger is ∼100 times
larger than in Palenzuela et al. (2010b), the energy flux is
only ∼8–2 times larger near the jets, thus yielding a collimated
luminosity that is ∼100 times smaller than the total one. As a
result, Paper I indicated that the detection of the dual jets at the
merger is difficult if not unlikely.
Here we provide additional information on the results pre-
sented in Paper I and discuss the details of our implementation of
the equations in which the FF condition is obtained via a damp-
ing scheme which drives the solution to satisfy the correct con-
dition. We show that this is important for a correct and accurate
description of the current sheets that can develop in the course
of the simulation. We also study in greater detail the three-
dimensional charge distribution produced as a consequence of
the inspiral and show that during the inspiral it has a complex
structure tracing the motion of the two BHs. Finally, we provide
quantitative estimates of the scaling of the EM emission with
frequency, with the diffused part having a dependence that is
the same as the GW one and that scales as L
non-coll
EM
≈ Ω
10/3−8/3
,
while the collimated one scales as L
coll
EM
≈ Ω
5/3−6/3
, thus with
a steeper dependence than previously estimated by Palenzuela
et al. (2010b).
This paper is organized as follows. In Section 2 we describe
the system of equations considered in our analysis, with par-
ticular emphasis on the treatment of the FF condition, while in
Section 3 we discuss the different routes to the calculation of the
EM radiated quantities. In Section 4 we present the astrophysical
setup of a BH binary merger, while Section 5 compares different
approaches for the enforcement of the FF condition. Section 6
is devoted to the presentation of the results, and, in particular,
to the computation of the luminosity. Finally, Section 7 presents
the conclusion of our work and the prospects for the detection
of an EM counterpart to SMBBHs.
In the rest of the paper, we set c = G = 1, adopt the standard
convention for the summation over repeated indices with Greek
indices running from 0 to 3, Latin indices from 1 to 3, and make
use of the Lorentz–Heaviside notation for the EM quantities, in
which all
√
4π factors disappear.
2. EVOLUTION EQUATIONS
We solve the combined system defined by the Einstein and
Maxwell equations and model either an isolated rotating BH or
a BH binary inspiralling in quasi-circular orbits. In both cases
we assume that there is an external FF magnetic field. More
specifically, we solve the Einstein equations
R
μν
−
1
2
Rg
μν
= 8πT
μν
, (1)
where R
μν
, g
μν
, and T
μν
are the Ricci, the metric, and the
stress-energy tensors, respectively. In addition, we solve the
following extended set of Maxwell equations (Komissarov
2007; Palenzuela et al. 2009b):
∇
μ
(F
μν
+ g
μν
Ψ) = I
ν
− κn
ν
Ψ, (2)
∇
μ
(
∗
F
μν
+ g
μν
Φ) =−κn
ν
Φ, (3)
where F
μν
is the Faraday tensor,
∗
F
μν
is its dual, I
μ
is the four-
current, and we have introduced a 3+1 slicing of spacetime, with
n
μ
being the unit (future oriented) timelike vector associated
with a generic normal observer to the spatial hypersurfaces.
The set of Maxwell Equations (2) and (3)isreferredtoas
“extended” because it incorporates the so-called divergence-
cleaning approach, originally presented in Dedner et al. (2002)
in flat spacetime, and which amounts to introducing two
additional scalar fields, Ψ and Φ, that propagate away the
deviations of the divergences of the electric and of the magnetic
fields from the values prescribed by Maxwell equations. Such
scalar fields are initialized to zero, but are driven into evolution
as soon as violations of the EM constraints are produced. The
total stress-energy tensor is composed of a term corresponding
to the EM field:
T
μν
f
≡ F
μ
λ
F
νλ
−
1
4
(F
λκ
F
λκ
)g
μν
, (4)
and of a term due to matter, T
μν
m
. However, because the EM field
is assumed to be FF, T
μν
f
T
μν
m
, and the total stress-energy
tensor is then assumed to be given entirely by Equation (4),
namely T
μν
≈ T
μν
f
. In the rest of our discussion we will use the
expression “electrovacuum” to denote the case when currents
and charges of the Maxwell equations are zero. Such a scenario
was extensively studied in M
¨
osta et al. (2010) and it will be used
here as an important reference. In the following we discuss in
more detail our strategy for the solution of the Einstein equations
and of the Maxwell system in an FF regime.
2.1. The Einstein Equations
For the solution of the Einstein equations we make use
of a three-dimensional finite-differencing code that adopts
a conformal-traceless “3 + 1” BSSNOK formulation of the
equations (see Pollney et al. 2007 for the full expressions in
vacuum and Baiotti et al. 2008 for the case of a spacetime with
matter). The code is based on the Cactus Computational Toolkit
(Allen et al. 2000) and employs adaptive mesh-refinement
techniques via the Carpet-driver (Schnetter et al. 2004). For
compactness we will not report here the details regarding the
adopted formulation of the Einstein equations and the gauge
conditions used, which can, however, be found in Pollney et al.
(2007, 2011).
We also note that recent developments, such as the use of
eighth-order finite-difference operators or the adoption of a
multiblock structure to extend the size of the wave zone, have
been recently presented in Pollney et al. (2009, 2011). Here,
however, in order to limit the computational costs and because
a very high accuracy in the waveforms is not needed, the multi-
block structure was not used and we have used a fourth-order
finite-difference operator with a third-order Implicit-Explicit
Runge–Kutta (RKIMEX) integration in time (see Section 2.3).
2

The Astrophysical Journal, 754:36 (17pp), 2012 July 20 Alic et al.
2.2. The Maxwell Equations
The Maxwell Equations (2) and (3) take a more familiar form
when expressed in terms of the standard electric and magnetic
fields as defined by the following decomposition of the Faraday
tensor in a 3+1 foliation:
F
μν
= n
μ
E
ν
− n
ν
E
μ
+
μναβ
B
α
n
β
, (5)
∗
F
μν
= n
μ
B
ν
− n
ν
B
μ
−
μναβ
E
α
n
β
, (6)
where the vectors E
μ
and B
μ
are purely spatial (i.e., E
μ
n
μ
=
B
μ
n
μ
= 0) and correspond to the electric and magnetic fields
measured by the normal (Eulerian) observers. The two extra
scalar fields Ψ and Φ introduced in the extended set of Maxwell
equations lead to two evolution equations for the EM constraints,
which, we recall, are given by the divergence equations
∇
i
E
i
= q, (7)
∇
i
B
i
= 0, (8)
where the electric current has been decomposed in the electric
charge density q ≡−n
μ
I
μ
and the spatial current J
i
≡ I
i
.
More specifically, these evolution equations describe damped
wave equations and have the effect of dynamically controlling
the possible growth of the violations of the constraints and of
propagating them away from the problematic regions of the
computational domain where they are produced.
In terms of E
μ
and B
μ
, the 3 + 1 formulation of Equations (2)
and (3) becomes (Palenzuela et al. 2010a)
D
t
E
i
−
ij k
∇
j
( αB
k
)+αγ
ij
∇
j
Ψ = αKE
i
− αJ
i
, (9)
D
t
B
i
+
ij k
∇
j
( αE
k
)+αγ
ij
∇
j
Φ = αKB
i
, (10)
D
t
Ψ + α ∇
i
E
i
= αq− ακ Ψ, (11)
D
t
Φ + α ∇
i
B
i
=−ακ Φ, (12)
D
t
q + ∇
i
( αJ
i
) = αKq, (13)
where
D
t
≡ (∂
t
− L
β
) and L
β
is the Lie derivative along the
shift vector β and K is the trace of the extrinsic curvature. The
charge density q can be computed either through the evolution
(Equation (13)) or by inverting the constraint (Equation (7)). For
simplicity, we choose the latter approach, which ensures that the
constraint (12) is automatically satisfied if Ψ = 0 initially and
effectively removes the need for the potential Ψ.
Exploiting now that the covariant derivative in the second term
of Equations (10) and (11) reduces to a partial derivative, i.e.,
ij k
∇
j
B
k
=
ij k
(∂
j
B
k
+ Γ
l
jk
B
l
) =
ij k
∂
j
B
k
, (14)
and using a standard conformal decomposition of the spatial
3-metric
˜γ
ij
= e
4φ
γ
ij
,φ=
1
12
ln γ, (15)
we obtain the final expressions for the extended Maxwell equa-
tions that we actually evolve
D
t
E
i
−
ij k
e
4φ
[(∂
j
α ) ˜γ
ck
B
c
+ α (4 ˜γ
ck
∂
j
φ + ∂
j
˜γ
ck
) B
c
+ α ˜γ
ck
∂
j
B
c
] = αKE
i
− αJ
i
, (16)
D
t
B
i
+
ij k
e
4φ
[(∂
j
α ) ˜γ
ck
E
c
+ α (4 ˜γ
ck
∂
j
φ + ∂
j
˜γ
ck
) E
c
+ α ˜γ
ck
∂
j
E
c
]+αe
−4φ
˜γ
ij
∇
j
Φ = αKB
i
, (17)
D
t
Φ + α ∇
i
B
i
=−ακ Φ. (18)
Clearly, the standard Maxwell equations in a curved background
are recovered for Φ = 0, so that the Φ scalar can then be con-
sidered as the normal-time integral of the standard divergence
constraint (8), which propagates at the speed of light and is
damped during the evolution.
As mentioned above, the coupling of the Einstein to the
Maxwell equations takes place via the inclusion of a nonzero
stress-energy tensor for the EM fields which is built in terms of
the Faraday tensor as dictated by Equation (4). More specifically,
the relevant components of the stress-energy tensor can be
obtained in terms of the electric and magnetic fields, that is as
τ ≡ n
μ
n
ν
T
μν
=
1
8π
(E
2
+ B
2
), (19)
S
i
≡−n
μ
T
μ
i
=
1
4π
ij k
E
j
B
k
, (20)
S
ij
≡ T
ij
=
1
4π
−E
i
E
j
− B
i
B
j
+
1
2
γ
ij
(E
2
+ B
2
)
, (21)
where E
2
≡ E
k
E
k
and B
2
≡ B
k
B
k
. The scalar function τ can
be identified with the energy density of the EM field, while the
energy flux S
i
is the Poynting vector.
As already discussed in the Introduction, we remark again
that the EM energies that will be considered here are so small
when compared with the gravitational binding ones that the
contributions of the stress-energy tensor to the right-hand side
of the Einstein Equations (1) are effectively negligible and thus
can be set to zero, reducing the computational costs. The fully
coupled set of the Einstein–Maxwell equations was considered
in Palenzuela et al. (2009a, 2010c) and the comparison with the
results obtained here suggests that for the fields below 10
8
G,
the use of the test-field approximation is fully justified.
2.3. Numerical Treatment of the Force-free Conditions
As noted before, within an FF approximation the stress-
energy tensor is dominated by the EM part and the contribution
coming from the matter can be considered zero. Following
Palenzuela et al. (2010a), the conservation of energy and
momentum, ∇
ν
T
μν
= 0, implies that also the Lorentz force
is negligible, i.e.,
0 =∇
ν
T
μν
≈∇
ν
T
μν
f
=−F
μν
I
ν
, (22)
which can also be written equivalently in terms of quantities
measured by Eulerian observers as
E
k
J
k
= 0, (23)
3

The Astrophysical Journal, 754:36 (17pp), 2012 July 20 Alic et al.
qE
i
+
ij k
J
j
B
k
= 0. (24)
Computing the scalar and vector product of the equations above
with the magnetic field B
i
, we obtain
E
k
B
k
= 0, (25)
J
i
= q
ij k
E
j
B
k
B
2
+ J
B
B
i
B
2
. (26)
The first relation (25) implies that the electric and magnetic
fields are orthogonal, while expression (26) defines the current,
whose component parallel to the magnetic field, namely J
B
≡
J
i
B
i
, needs to be defined via a suitable Ohm law. From the
numerical point of view, specific strategies must be adopted in
order to enforce the FF constraints expressed by Equations (25)
and (26). In fact, even though such constraints are exactly
satisfied at time t = 0, there is no guarantee that they will
remain so during the evolution of the system.
The approach introduced by Palenzuela et al. (2010a)to
enforce the constraints (25) and (26) consists in a modification
of the system at the discrete level, by redefining the electric field
after each timestep in order to remove any component parallel to
the magnetic field. In other words, after each timestep the newly
computed electric field is “cleaned” by imposing the following
transformation (Palenzuela et al. 2010a)
E
i
→ E
i
− (E
k
B
k
)
B
i
B
2
. (27)
In addition, the current is computed from Equation (26)af-
ter setting J
B
= 0. An alternative approach, introduced in
Komissarov (2011) and then in Lyutikov (2011), uses the
Maxwell equations to compute
D
t
(E
k
B
k
), which has to van-
ish according to Equation (25). Using Equations (10) and (11)
it is then easy to obtain the following prescription for J
B
:
J
B
=
1
α
[B
i
ij k
∇
j
(αB
k
) − E
i
ij k
∇
j
(αE
k
)]. (28)
Without further modifications, however, this approach leads to
large violations of the FF constraint (25) in long-term numerical
simulations, as it does not provide a mechanism for imposing
the constraint at later times.
As we will show later on, both approaches (27) and (28)
are not fully satisfactory and, as a consequence, here we
present an alternative method, which takes inspiration from the
treatment of currents (and related stiff source terms) in resistive
magnetohydrodynamics. The idea of introducing a suitable Ohm
law was proposed in Komissarov (2004) and then in Palenzuela
et al. (2010a), but it has not been used so far in numerical
simulations, due to the presence of stiff terms which appear as a
result. In practice, our continuum approach is equivalent to the
insertion of suitable driver terms, so that the parallel component
J
B
is computed from an Ohm law of the type
J
B
= σ
B
E
k
B
k
, (29)
where σ
B
is the anisotropic conductivity along the magnetic-
field lines. This additional term in the current acts like a damping
term in the evolution ∂
t
(E
k
B
k
), and enforces the constraint (25)
on a timescale 1/σ
B
.Forσ
B
sufficiently large, one can ensure
that the FF constraint (25) is always satisfied. In the simulations
presented in this paper, we choose σ
B
> 1/Δt, where Δt is the
timestep on the finest refinement level. The resulting hyperbolic
system with stiff terms is solved using a third-order RKIMEX
time integration method with the technical implementation
following the one discussed in Palenzuela et al. (2009b) and
with additional details presented in the Appendix.
An additional problem in the numerical treatment of the
FF approach is represented by the development of current sheets,
namely of regions where the electric field becomes larger than
the magnetic field, such that the condition
B
2
− E
2
> 0 (30)
is violated. If this happens, and in the absence of a proper Ohm
law responsible for the resistive effects, the Alfv
´
en wave speed
becomes complex and the system of FF equations is no longer
hyperbolic (Komissarov 2004). Under realistic conditions, one
expects that in these regions an anomalous and isotropic
resistivity would restore the dominance of the magnetic field.
A solution to this problem was proposed in Komissarov (2006),
where the velocity of the drift current was modified in order
to ensure that it is always smaller than the speed of light. This
leads to the following prescription for the current:
J
i
= q
ij k
E
j
B
k
B
2
+ E
2
+ J
B
B
i
B
2
, (31)
which should be compared with Equation (26) and has the net
result of underestimating the value of the current.
An alternative solution to the numerical treatment of current
sheets consists in a modification of the system again at the
discrete level (Palenzuela et al. 2010a). In practice, after each
timestep a correction is applied “by hand” to the magnitude of
the electric field in order to keep it smaller than the magnetic
field, i.e.,
E
i
→ E
i
(1 − Θ)+Θ
B
2
E
2
, (32)
with Θ = 1 when B
2
− E
2
< 0 and Θ = 0 otherwise.
Our strategy, however, differs from both the previous ones
and follows the same philosophy behind the choice of the driver
defined by Equation (29). We therefore introduce a second
driver in Ohm law, which will act as a damping term for the
electric field in those cases when E
2
>B
2
. This additional
term, combined with the prescription for the parallel part of the
current (29), leads to the following effective Ohm law:
J
i
= q
ij k
E
j
B
k
B
2
+ σ
B
(E
k
B
k
)
B
i
B
2
− σ
B
(B
2
− E
2
)E
i
E
2
B
2
.
(33)
Expression (33) shows therefore that in normal conditions, i.e.,
when B
2
− E
2
0, the last term introduces a very small
and negative current along the direction of the electric field.
However, should a violation of the condition (30) take place, a
positive current is introduced, which reduces the strength of the
electric field and restores the magnetic dominance.
In Section 5 we will compare the different prescriptions for
the enforcement of the FF condition and show that, in contrast to
recipes (27) and (32), our suggestions (29) and (33) yield both
and accurate and a smooth distribution of the EM currents.
4

The Astrophysical Journal, 754:36 (17pp), 2012 July 20 Alic et al.
3. ANALYSIS OF RADIATED QUANTITIES
The calculation of the EM and gravitational radiation gen-
erated during the inspiral, merger, and ringdown is an impor-
tant aspect of this work as it allows us to measure the amount
correlation between the two forms of radiation. We compute
the gravitational radiation via the Newman-Penrose curvature
scalars. In practice, we define an orthonormal basis in the three-
dimensional space (
ˆ
r,
ˆ
θ,
ˆ
φ), with poles along ˆz. Using the nor-
mal to the slice as timelike vector
ˆ
t, we construct the null or-
thonormal tetrad {l , n, m,
m}:
l =
1
√
2
(
ˆ
t +
ˆ
r), n =
1
√
2
(
ˆ
t −
ˆ
r), m =
1
√
2
(
ˆ
θ + i
ˆ
φ), (34)
with the bar indicating a complex conjugate. Adopting this
tetrad, we project the Weyl curvature tensor C
αβγ δ
to obtain
Ψ
4
≡ C
αβγ δ
n
α
¯m
β
n
γ
¯m
δ
, that measures, ideally at null infinity,
the outgoing gravitational radiation. For the EM emission, on the
other hand, we use two equivalent approaches to cross-validate
our measures. The first one uses the Newman-Penrose scalars
Φ
0
(for the ingoing EM radiation) and Φ
2
(for the outgoing
EM radiation), defined using the same tetrad (Teukolsky 1973):
Φ
0
≡ F
μν
l
ν
m
μ
, Φ
2
≡ F
μν
m
μ
n
ν
. (35)
By construction, the Newman-Penrose scalars Ψ
4
, Φ
0
, Φ
2
are
dependent on the null tetrad (34), so that truly unambiguous
scalars are measured only at very large distances from the
sources, where inertial observers provide preferred choices. Any
measure of these quantities in the strong-field region is therefore
subject to ambiguity and risks producing misleading results. As
an example, the EM energy flux does not show the expected
1/r
2
scaling when Φ
2
and Φ
0
are measured at distances of
r 20 M, as used in Palenzuela et al. (2010a, 2010b), which
is instead reached only for r 100 M. As we will show in
Section 6, this fact is responsible for significant differences in
the estimates of the non-collimated EM emission.
The use of a uniform magnetic field within the computational
domain has a number of drawbacks, most notably, nonzero
initial values of Φ
2
, Φ
0
. As a result, great care has to be
taken when measuring the EM radiation. Fortunately, we can
exploit the linearity in the Maxwell equations to distinguish the
genuine emission induced by the presence of the BH(s) from
the background one. Following Teukolsky (1973), we compute
the total EM luminosity as a surface integral across a 2-sphere
at a large distance:
L
EM
= lim
r→∞
1
2π
r
2
(|Φ
2
|
2
−|Φ
0
|
2
) dΩ, (36)
which results straightforwardly from the integration of the
component of EM stress-energy tensor (4) along the time-
like vector n
μ
and the normal direction to the large
2-sphere (namely, the flux of the Poynting vector in
Equation (19) through the 2-sphere). The term Φ
0
in
Equation (36) has been maintained (it disappears at null infinity)
to account for the possible presence of an ingoing component
in the radiation at finite distances. In particular, Equation (36)
shows that the net flux is obtained by adding (with the appropri-
ate sign) the respective contributions of the outgoing and ingoing
fluxes. More specifically, in terms of the complex scalars Φ
2
and
Φ
0
, the outgoing net flux is obtained by subtracting the square of
their respective moduli. In the specific scenario considered here,
where a nonzero non-radiative component of the magnetic field
extends to large distances, expression (36) must be modified.
More specifically we rewrite it as
L
EM
= lim
r→∞
1
2π
r
2
(|Φ
2
−Φ
2,B
|
2
−|Φ
0
−Φ
0,B
|
2
) dΩ, (37)
where Φ
2,B
and Φ
0,B
are the values of the background scalars
induced by the asymptotically uniform magnetic-field solution
in the time-dependent spacetime produced by the binary BHs.
Under the assumption of a vanishing net ingoing radiation, i.e.,
Φ
0
≈ Φ
0,B
and of stationarity of the background field, i.e.,
Φ
2,B
≈ Φ
0,B
, expression (37) can also be rewritten as (Neilsen
et al. 2011;Ruizetal.2012)
L
EM
= lim
r→∞
1
2π
r
2
(|Φ
2
− Φ
0
|
2
) dΩ. (38)
Although Equation (38) does not represent, at least in a strict
physical and mathematical sense, a valid expression for the
emission of EM radiation in generic scenarios, it can provide a
useful recipe whenever the assumed approximations made above
are actually fulfilled. In Section 6 we will assess to what degree
this is the case for the specific scenario and model considered
here.
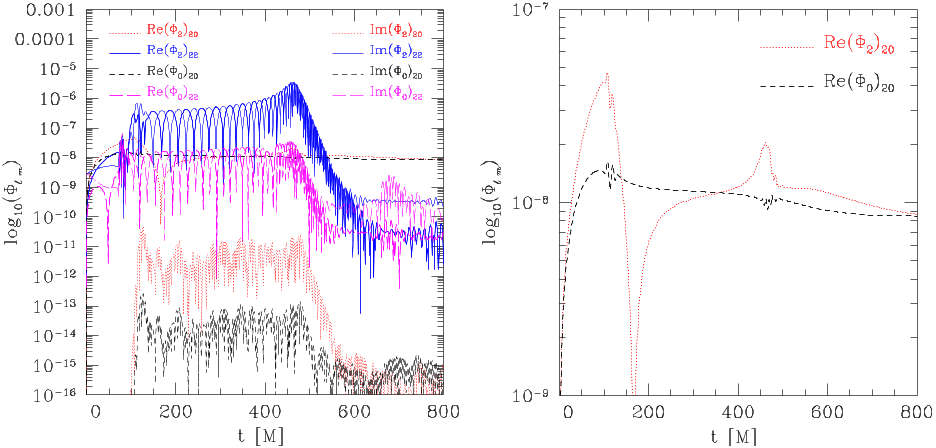
The choice of the background values of the Newman-Penrose
scalars Φ
2,B
and Φ
0,B
plays a crucial role in measuring correctly
the radiative EM emission, since these quantities are themselves
time dependent and cannot be distinguished, at least a priori,
from the purely radiative contributions. This introduces an
ambiguity in the definition of Φ
2,B
and Φ
0,B
, which can,
however, be addressed in at least two different ways. The first
one consists in assuming that the background values are given by
the initial values, and further neglecting their time dependence,
namely setting
Φ
2,B
= Φ
2
(t = 0), Φ
0,B
= Φ
0
(t = 0). (39)
Since all the m = 0 multipoles of the Newman-Penrose scalars
are not radiative, a second way to resolve the ambiguity is to
remove those multipole components from the estimates of the
scalars, namely, of defining
Φ
2,B
= (Φ
2
)
,m=0
, Φ
0,B
= (Φ
0
)
,m=0
, (40)
where (Φ
2
)
,m=0
refer to the m = 0 modes of the multipolar
decomposition of Φ
2
( 8 is sufficient to capture most of the
background). Note also that because the m = 0 background
is essentially time independent (after the initial transient),
the choice (40) is effectively equivalent to the assumption that
the background is given by the final values of the Newman-
Penrose scalars as computed in an electrovacuum evolution
of the same binary system. While apparently different, ex-
pressions (39) and (40) lead to very similar estimates (see
Section 6.1) and, more importantly, they have a simple interpre-
tation in terms of the corresponding measures that they allow.
The second approach that we have followed for the compu-
tation of the emitted luminosity is the evaluation of the flux of
the Poynting vector across a 2-sphere at large distances in terms
of the more familiar 3+1 fields E
i
and B
i
in Equation (19). Of
course, such evaluation is adequate only far from the binary.
The purpose of implementing both versions of the luminosity
calculation, which are conceptually equivalent but differ in the
technical details, is precisely to quantify the error introduced by
5