Adaptive Strategies for Dynamic Pricing Agents
Sara Ramezani, Peter A. N. Bosman, and Han La Poutr
´
e
CWI, Dutch National Institute for Mathematics and Computer Science
P.O. Box 94079, NL-1090 GB, Amsterdam, The Netherlands
Email: S.Ramezani, Peter.Bosman, Han.La.Poutre@cwi.nl
Abstract—Dynamic Pricing (DyP) is a form of Revenue
Management in which the price of a (usually) perishable good
is changed over time to increase revenue. It is an effective
method that has become even more relevant and useful with
the emergence of Internet firms and the possibility of readily
and frequently updating prices. In this paper a new approach
to DyP is presented. We design adaptive dynamic pricing
strategies and optimize their parameters with an Evolutionary
Algorithm (EA) offline while the strategies can deal with
stochastic market dynamics quickly online. We design two
adaptive heuristic dynamic pricing strategies in a duopoly
where each firm has a finite inventory of a single type of
good. We consider two cases, one in which the average of a
customer population’s stochastic valuation for each of the goods
is constant throughout the selling horizon and one in which the
average customer valuation for each good is changed according
to a random Brownian motion. We also design an agent-based
software framework for simulating various dynamic pricing
strategies in agent-based marketplaces with multiple firms
in a bounded time horizon. We use an EA to optimize the
parameters for each of the pricing strategies in each of the
settings and compare the strategies with other strategies from
the literature. We also perform sensitivity analysis and show
that the optimized strategies work well even when used in
settings with varied demand functions.
I. INTRODUCTION
Dynamic Pricing (DyP) is a form of Revenue Manage-
ment (RM) that involves changing the price of goods or ser-
vices over time with the aim of increasing revenue. Revenue
management is a much broader term that refers to various
techniques for increasing revenue of (usually) perishable
goods or services. RM particularly became popular within
the airline industry after the deregulation of the industry in
the United States in the late 1970’s [18].
Today, the Internet provides exceptional opportunities
for practicing RM and particularly DyP. This is due both
to the amount of data available and the restructuring of
price posting procedures. Thus, the Internet can facilitate
offering different prices for different customers and posting
new prices with minimum extra costs. This also allows for
the increased use of intelligent autonomous agents in e-
commerce, agents designed for automatically buying, sell-
ing, price comparison, bargaining, etc..
Most RM methods exploit the differences in different cus-
tomers’ valuations of a good or changes in these valuations
in time to boost revenue. This has led to different methods of
distinguishing between customers based on their valuation
for the goods, such as fare class distinction, capacity control,
dynamic pricing, auctions, promotions, coupons, and price
discrimination methods such as group discounts [18].
Here we focus on dynamic pricing [7]. By changing prices
in time, firms can ask for the price that yields the highest
revenue at each moment. This allows them to distinguish
between customers in cases where customers with different
utilities buy at different times, as well as exploit the changes
of valuation of the same customers in time. Many RM
methods can be categorized as dynamic pricing, be it the
end-of-season markdown of a fashion retailer, or the inflated
last-minute price of a business-class flight ticket. The main
question is when and how to change the prices in order
to obtain the most revenue. This depends on the market
structure and dynamics, most importantly, on the customer
demand rate and how it changes in time.
In this paper we study dynamic pricing of a limited supply
of goods in a competitive finite-horizon market. We design
and implement an interactive agent based marketplace where
the agents are the firms who wish to increase their revenue
using dynamic pricing strategies. We study two cases, one
in which the customers’ valuation for the products follow
the same valuation throughout the selling horizon and one
in which the average of their valuations follow a random
Brownian motion over time.
We design two adaptive pricing strategies and use learning
to optimize them. The execution of the strategies is not
computationally intensive (O(1) complexity) and they are
understandable from a practical perspective. The strategies
use only the observed market response to set new prices at
each point in time. The parameters used in each strategy
are then optimized using an Evolutionary Algorithm (EA)
[3]. A simulation software has been implemented that can
generate and simulate dynamic pricing strategies in various
oligopolistic markets. The EA uses this simulator as a black
box, and optimizes the parameters for a given strategy using
the obtained revenue as the fitness criteria. So on one hand,
the strategies are capable of very fast adaptive decision
making in run-time, and on the other hand their parameters
are optimized offline to tune them for a more specific setting.
In many real world applications, some general knowledge
of the market dynamics exists beforehand, although it may
be different from what will actually happen, both because

of inaccuracies in the estimations and predictions and unex-
pected changes to the market. Using our proposed approach,
this knowledge can be used for offline learning, to optimize
the parameters of the strategies before the actual selling
starts. Also, because of the adaptiveness of the proposed
pricing strategies, any deviations from the expected dynam-
ics of the market will be detected quickly and accounted
for by the strategy online, and thus the strategies also work
reasonably well in various market settings different from
what they have been tuned for.
In the strategies we present, the selling agents do not
assume the demand to have an a priori structure, though the
EA uses the market simulation with a particular structure to
optimize the performance of the strategy over the space of
its parameters. Thus, information of the demand structure is
passed to the selling agents implicitly through the parame-
ters. The strategies are adaptive in the sense that they detect
changes in the market and adjust their prices accordingly.
Hence they can effectively deal with market changes.
In order to evaluate our strategies’ performance, we com-
pare them to a number of strategies previously studied in
the DyP literature. We show that our strategies outperform
a fixed price (FP) strategy that is optimized offline. This
is significant, because FP strat egies perform very well in
many configurations [9]. It should be noted here that in most
other models a FP strategy is actually the optimal strategy
and DyP is used to find this optimal fixed price, but in our
case no fixed price is optimal due to the combination of
competition, finite inventory, and a finite time horizon. This
can also be shown by the fact that our strategies outperform
the offline-optimized FP (that is very close to the actual best
possible fixed price). The same features make the analytical
computation of the best solution in our model intractable,
requiring experimentation to evaluate our strategies. In fact,
a benefit of using simulations is that we are able to tackle
more complicated models that are too difficult to approach
theoretically.
Furthermore, the strategies also perform better than the
optimized versions of the derivative follower (DF) learn-
ing algorithm that change the price in the same direction
(increasing or decreasing) as long as the revenue keeps
increasing, and then changes the price change direction.
Such algorithms have previously been used successfully in
DyP settings [4], [6], [14]. Our proposed strategies are also
compared to the Goal Directed (GD) strategy of [6] which is
particularly similar to one of our strategies. Both strategies
outperform the GD strategy for which the only parameter,
the initial price, is optimized for the given setting.
Finally, we show that optimized adaptive strategies still
perform reasonably well when various changes are made
to the market configuration after the learning phase. For
this means, we evaluate the performance of a strategy
with parameters optimized for a given configuration, on a
stochastically varied configuration. The obtained revenue
is then compared with the revenue obtained by using the
same strategy with parameters optimized for the varied
setting. This can give us the regret of wrongly estimating
the market structure. The variations in configuration that we
study include altering the demand function by changing the
customer/good ratio.
II. RELATED WORK
DyP has been a very active research area in recent
years. Many studies try to learn the demand structure, or
the parameters for a known demand function, on the fly.
They typically use part of the selling horizon for exploring
the market, trying out the demand rate for different prices
in a systematic way, and another portion of the time for
exploiting the market, using the best price(s) based on their
estimates [2], [8]. Others use statistical learning methods and
heuristics based on mathematical estimations of the optimal
price [1]. While most DyP models are monopolies, there
are some that model competitors in the marketplace as well
[14], [15], [16]. In this work we deal with a duopoly market,
though the firm does not model a competitor explicitly.
Works that are similar to ours in experimenting with
heuristic strategies by simulation are fewer. The Information
Economics group at IBM has investigated the effect of
interacting pricing agents which they call pricebots in a
number of works (see [14] for a survey). In some, they use
use game-theoretic analysis and experiment with heuristics
that aim at achieving the optimal equilibrium price [11].
They focus on the market dynamics and pricing patterns
that arise when using these strategies against each other.
They also study shopbots [10], strategic buyer agents, and
pricing where agents may be differentiated horizontally or
vertically based on their preferences for different attributes
of a product. Some of the algorithms discussed in these
works rely on more information than can be obtained from
the market simulations only, but we have compared our work
to the FP and a few versions of the DF strategies, both of
which are used in these works.
Multi-attribute DyP is also discussed in [5] and [13]. In
[13] a heuristic method for dynamic pricing is presented
which consists of a preference elicitation algorithm and a
dynamic pricing algorithm. The method is then compared to
a DF algorithm and the GD algorithm from [6], their model
differs from the one we use in the existence of multiple
attributes (we consider a single attribute here, the price) and
also because they have a finite number of identifiable buyers
(compared to our infinite population of one-time buyers).
Their algorithms, although similar to ours in fast online
decision making and the use of simulation for the evaluation,
were not directly comparable to the strategies in our current
model due to the strong dependence on these differences,
the simplification of which would significantly undermine
the strengths of their strategies.

In [4], a heuristic Model Optimizer (MO) method is
designed and compared to a DF pricing strategy. The MO
strategy uses information from the previous time intervals
for a more detailed model of the demand, and solves a
non-linear equation in each time step using a simplex hill-
climbing approach. This heuristic strategy differs from ours
in its online computational complexity, which is much higher
than ours due to the online optimization.
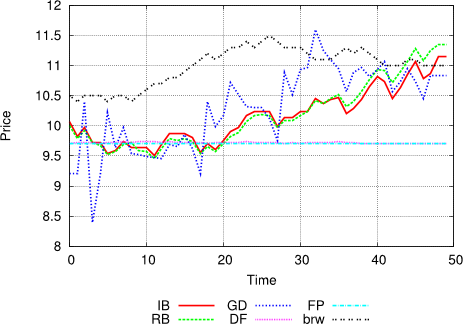
In [6] a DF algorithm and an inventory-based GD algo-
rithm are used in a number of simulations to show how they
actually behave in a market and in which scenarios each
one is useful. We compare our strategies with both of these
strategies, because they are both compatible with our model
and comparable with our strategies in their computational
intensity and the information they use.
In [17], a few different EA methods are used to solve a
dynamic pricing problem. Their approach is not comparable
to ours since they use their optimizer to optimize actual
prices for a dynamic pricing model for a small number
(less than 10) of time steps. A method similar to [17]
is not useful in our stochastic model because optimizing
prices using an EA would lead to an over-fitted solution
that works better than the adaptive strategies only for the
instances (see definition 2 in section IV) it is optimized for
and considerably worse on average. It is also far more time-
consuming when considering a larger number of time steps.
III. MODEL
We have a market with two competing firms. The revenue
(sum of price of items sold) of one of the firms is optimized
using DyP. Each firm can change the price of its goods at
the start of equi-distant time intervals.
A. Firms
We have a finite number, m, of firms, {0, 1, . . . , m − 1}.
We refer to firm j’s good type as g
j
. The firm starts off with
an initial inventory Y
j
of its product and the capacity left of
the good at time t is denoted by y
j
(t) (the t can be omitted
if there is no chance of ambiguity).
The model is a finite horizon model, the goods left at the
end of each time step are transferred into the next and all
goods are lost at the end of the whole time span. Each firm
announces a selling price, p
j
(t), for each good type in each
time interval t. A cost for each good type, cr
j
, serves as a
reserve price for goods of that type.
B. Customers
1) Preferences: The customers specify their preferences
using non-negative cardinal utilities that are exchangeable
with monetary payments. Each customer has a valuation
function that determines these utilities. Customers are unit-
demand, they only have preferences on sets consisting of one
item, so their valuation functions are defined as v : G → R
+
.
Thus, customers have to specify only a single number for
each good type and its valuation for getting more than one
item is always zero. Thus, a customer’s utility for getting an
item is equal to the difference between its valuation for the
item and the item’s price, which is u
j
(t) = v(g
j
) − p
j
(t)
for firm j’s good at time t.
2) Population: We model the customer populations as an
unbounded population. This means that the distribution of
customers does not change after an item is sold. Also, the
valuations of all of the customers for each unit of each of the
good types follow the same distribution. This distribution,
which is denoted by P r
j,t
for firm j’s good at time t, may
or may not change in time.
These distributions are all normal distributions. We con-
sider two settings, in the first setting the normal distribution
is the same for each good type and customer segment
pair throughout the time horizon (so the t can be omitted
from P r
j,t
). In the second setting, which we refer to as
the Brownian setting, the mean of the each of the P r
j,t
distributions changes over time, following a basic model
of Brownian motion: the mean increases by a constant
amount (b), decreases by the same constant amount, or does
not change, each of these cases happening with equal (
1
3
)
probability. This allows for some structured dynamism in
the demand pattern in the model.
3) Customer arrival: The number of customers that ar-
rive in each time step follows a Poisson process with a con-
stant intensity a. The firms may be aware of the parameter
of this process when making their pricing decisions. In each
time interval, the customers arrive consecutively after the
firms have set their prices. They may or may not buy a
product based on their choice function and, in any case,
leave the market afterwards.
4) Choice Model: At any time t that a customer has to
make a purchase decision, it will buy one of good g
∗
offered
by firm f
∗
∈ arg max
j
{u
j
(t)|u
j
(t) > 0}, if it exists, i.e.
the item for which it has the highest utility if all items are
not priced higher than he is willing to pay, with probability
1 − λ and does not purchase anything with probability λ.
The λ factor is to model a general chance for a purchase not
occurring, this is close to the natural behavior of customers
in many contexts. Note that the effect of the λ can also be
achieved by changing the arrival rate when we are using
a Poisson arrival process, but it is not so with all arrival
models. If g
∗
does not exist, the customer will not make a
purchase. Ties are broken randomly.
As is evident from the model, the customers are myopic
(greedy) and purchase only based on current utilities, not
any prediction of what will happen next.
C. Modeling Time
In any dynamic pricing model, by definition, the firms
should be able to adjust their prices in time. While changing
prices at any particular moment may become more plausible,
particularly with internet firms, it is still more common in

the literature for the change of prices to occur in fixed
time intervals. We suppose that there are T time intervals,
numbered from 1 to T successively. At the start of each time
interval, all firms set the prices for their goods.
IV. MARKET SIMULATION
We have developed software for simulating a marketplace
described in the previous section. The software uses an event
queue to keep track of two types of events: pricing events,
firms setting the price for each of their item types at the
beginning of each time period, and customer arrival events.
Some notation that helps describe the experiments in the
following section is defined here.
Definition 1 (Configuration): A configuration is a model
where all parameters are set. These parameters consist of the
properties of the firms (costs of goods, initial stock, etc.) and
the valuation distributions and arrival rate of the customers.
Definition 2 (Instance): An instance of the problem is
a specific configuration together with samplings for the
stochastic variables (i.e. a fixed random seed for the pseudo
random generator in the software).
Definition 3 (Pricing Strategy): A pricing strategy, or
simply strategy, is a function that given a fixed number of
parameters, sets a new price for a unit of the firm’s good in
each time step. The function can also depend on the previous
events that have occurred in the market. We assume here that
the firm is aware of the previous customers’ behavior and
previous prices, and that the firm knows the customer arrival
rate, but nothing about the customers’ valuation functions.
All strategies are deterministic.
Based on the above definitions, an instance of the problem
is deterministic given the firms’ strategies, i.e. will yield the
same results when the firms use the same strategies, while
a configuration alone does not contain enough information
to determine an outcome.
Definition 4 (Simulation): By a simulation, we designate
a single execution of a particular instance of the problem
with fixed strategies for the firms.
Definition 5 (Batch run): By a batch run, or simply
batch, consisting of n simulations, we mean the simulation
of n different instances of the problem that share the same
configuration and use the same strategy for each of the firms
throughout the n instances.
V. ADAPTIVE HEURISTIC STRATEGIES
We present two heuristic pricing strategies in this section.
A. The Inventory Based (IB) Strategy
The first strategy is one that adaptively adjusts the prices
for a firm based on the number of goods it has left and
the number of goods that it has sold in the previous time
interval, we call it the Inventory Based (IB) strategy.
In each time step, the strategy retains the previous price
if the rate of items sold in the previous time interval is
Algorithm 1 InventoryBasedStrategy(initialPrice,
noChangeThreshUp, noChangeThreshDown, maxIncPer-
cent, maxDecPercent)
1: if time = 0 then
2: price ← initialP rice
3: return price
4: if numLeft = 0 then
5: return lastP rice
6: if pastCustomers = 0 then
7: pastCustomers ← 1
8: pastSold ← pastSold ×
aveCustomers
pastCustomers
9: α ←
pastSold×timeLeft
numGoodsLeft
10: if α < 1 then
11: ∆ = α − 1
12: else
13: ∆ = 1 −
1
α
14: if |∆| < 0 then
15: if ∆ < noChangeT hreshDown then
16: price ← lastP rice
17: else
18: price ← lastP rice(1 + ∆ × maxDecP ercent)
19: else
20: if ∆ < noChangeT hreshUp then
21: price ← lastP rice
22: else
23: price ← lastP rice(1 + ∆ × maxIncP ercent)
24: return price
close to the rate needed to sell all the items by the end of
the time horizon (this “closeness” is controlled by the pa-
rameters noChangeT hreshUp noChangeT hreshDown).
It increases the price if too many items have been sold
in the previous interval and decreases it if too little have
been sold. The maxDecP ercent and maxIncP ercent
parameters along with the distance that the sales rate has
from the expected sales rate control the amount of change
in price in each time step. The other parameter used in this
strategy is intialP rice, the price the firm uses in the first
time interval. The details of the algorithm of this strategy
can be seen in algorithm 1.
In algorithm 1, pastSold is the number of items sold
in previous time step, and numGoodsLef t is the number
of items left in the inventory. timeLef t is the number of
time steps left in the selling horizon, and pastP rice is
the price of a unit of the good in the previous time step.
Finally, pastCustomers is the total number of customers
in the previous time step and aveCustomers is the average
number of customers per time step (same as a).
In line 8, the number of items sold in the past time interval
is normalized by the average number of customers arriving
in each time step and the number of goods left to factor
out the stochasticity as much as possible. Note that this is

a dynamic indicator updated in the beginning of each time
step, so it will take into account the current state of the
agent. In line 9, α is defined as an indicator for determining
how fast the inventory would be exhausted if the sales would
go on with the current rate. If α is smaller than one, then
the sales rate is too slow, and if it is larger than one, the
the inventory would be exhausted sooner than the end of
the time horizon, so there is an opportunity for increasing
the price. The parameter ∆ is then (in the if-then statement
starting from line 10) defined as a normalized version of α
that is negative if the sales rate is too low and positive if it is
too high. The if-then statement starting from line 14 is where
the final pricing decision is made. If the absolute value of
∆ is smaller than the respective threshold for positive or
negative threshold parameter, i.e. if the sales rate is close
enough to the desired rate, then the price is not changed
otherwise it is changed proportional to ∆, and with regards
to the maximum allowable change rate.
B. The Revenue Based (RB) Strategy
The Revenue Based (RB) strategy uses an estimation of
a desirable price to estimate the price in each time step.
It uses the revenue per customer (RPC) criterion (which
considers all customers, even the ones that did not buy
from the firm) to assess the revenue obtained when using
a particular price and compares that to the RPC needed to
finish the inventory by the end of the selling horizon. The
algorithm for this strategy can be seen in algorithm 2. The
additional parameters used in this strategy are expP rice,
the expected price used in the estimation of the expected
RPC, and the maximum amount the price can change per
time step. These variables are also used: RP , the revenue
per customer in the previous time step, and the expected
RPC, used as a control parameter, expRP C.
Algorithm 2 RevenueBasedStrategy(initialPrice, expPrice,
maxDelta)
1: if time = 0 then
2: price ← initialP rice
3: return price
4: expRP C ←
numGoodsLeft×expP rice
timeLeft×aveCustomers
5: if numLeft = 0 then
6: return lastP rice
7: if pastCustomers = 0 then
8: pastCustomers ← 1
9: RP C ←
pastSold×lastP rice
pastCustomers
10: α ←
RP C
expRP C
11: if α ≤ 1 then
12: ∆ ← α − 1
13: else
14: ∆ ← 1 −
1
α
15: price ← lastP rice + ∆ × maxDelta
16: return price
In this algorithm, the expRP C (defined in line 4) variable
is the expected revenue per customer for the rest of the
selling horizon, provided that the firm sells with the ex-
pected price, expP rice, that is one of the input parameters.
Then the RP C parameter is the revenue obtained for each
customer in the previous time step (regardless of whether
they make a purchase or not). In this algorithm, α is defined
as the ratio between the expected RPC and the RPC from
the previous time step. Here, also, ∆ is a normalization of
α, positive if the expected revenue is higher than expected
and negative if it is lower (line 11), and the price changes
proportional to the magnitude of ∆. Note that here the lower
than expected revenue is attributed to a price that is too high,
thus prohibiting many customers form making a purchase.
This is not always the case though, but this can be a safe
assumption when the initial price and expected price are
chosen properly, as we can see from the experimental results.
Note that both strategies depend only on information from
the sales in one previous time step. Also, the parameters
are designed as to sustain a certain amount of stability in
the price. This is both a means to control the effects of the
stochastic noise causing sudden jumps in the price (specially
since the changes depend on one previous time step only),
and because too much price fluctuation is not desirable from
the customers’ perspective. Also, in all strategies reported
in this work, the previous price is kept if there are no
more goods to be sold. This has no effect on the simulation
because customers will not be given the option to buy from
firms that have no goods left.
C. Computing the Parameters
We want to have settings for the parameters of the strate-
gies that we have defined such that the strategies perform
well. The numerical optimization task associated with this is
generally not easy because it is the outcome of a non-trivial
simulation that we want to optimize. The problem at hand
can thus be seen as a black-box optimization problem with
unknown difficulty. We therefore need black-box optimiza-
tion algorithms that are capable of tackling a large class of
problems effectively. The algorithm of our choice is called
AMaLGaM. AMaLGaM is essentially an Evolutionary Al-
gorithm (EA) in which a normal distribution is estimated
from the better, selected solutions and subsequently adapted
to be aligned favorably with the local structure of the search
space. New solutions are then constructed by sampling the
normal distribution. A parameter-free version of AMaLGaM
exists that can easily be applied to solve any optimization
problem. This version was recently found to be among the
most competent black-box optimization algorithms [3], [12].
In order to tune the experiments for the EA, which is
not designed to handle stochasticity on one hand, and not
to over-fit a single instance of the problem on the other,
we use the following method. The fitness used in the EA
is the average revenue obtained from a batch run of 100