




read more









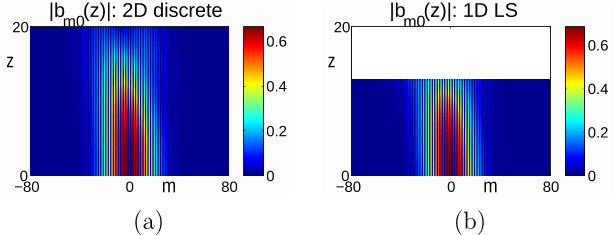

Due to the z-dependence of the coefficients of the NLS equation, the edge soliton exhibits slow modulation in its amplitude and width.
As with the traditional, constant coefficient, focusing NLS equation, nonlinearity balances dispersion to produce nonlinear edge solitons.
The waveguides play the role of a pseudomagnetic field, and in certain parameter regimes, the edge waves are found to be nearly immune to backscattering.
The authors also note that after dropping primes, the dimensionless variables x, y, z, ψ are used; these dimensionless variables should not be confused with the dimensional variables in Eq. (1).
A nonconstant coefficient (‘time’-dependent) one-dimensional nonlinear Schrödinger (NLS) equation governing the envelope of the edge modes is derived and is found to be an effective description of nonlinear traveling edge modes.
However when edges and a ‘pseudo-field’ are present, remarkable changes occur and long lived, persistent linear and nonlinear traveling edge waves with little backscatter appear.
4. Thus the localization interval IZ(ω) corresponds to the vertical slice through the shaded region at fixed ω, and the existence interval Ip = (ω−, ω+) of pure edge modes is bounded by the two solid white lines.
For the pseudo-field Eq. (6)A = (A1(z), A2(z)) = κ(sinΩz,− cosΩz) = κ(sinZ,− cosZ), Z = ǫz,taking Ωz∗ = ǫ where ǫ = 0.1 leads to Ω = 14.8 rad/m and the period T = 2π Ω = 42 cm.
Taking a discrete Fourier transform in m, i.e. letting amn = ane imω and bmn = bne imω, yields the simplified systemi∂zan + e id·AL−bn + σ|an|2an = 0, (12) i∂zbn + e −id·AL+an + σ|bn|2bn = 0, (13)whereL−bn = (bn + ργ∗(z;ω)bn−1) (14) L+an = (an + ργ(z;ω)an+1) (15)γ(z;ω) = 2eiϕ+(z) cos(ϕ−(z)− ω) andϕ+(z) = (θ2(z) + θ1(z))/2, ϕ−(z) = (θ2(z)− θ1(z))/2.Since γ(z;ω + π) = −γ(z;ω), if (an(z), bn(z)) is a solution of Eqs. (12–13) at any given ω, then (−1)n(an(z), bn(z)) is a solution of Eqs. (12–13) at ω + π.
the dispersion relation of edge modes in Fig. 2(a) breaks up into multiple segments near ω = 0, π. Also, in Fig. 2(b) there are scattered eigenvalues near α = 0 for ω immediately outside Ip = (ω−, ω+).
In the rapidly varying case [28], the associated NLS equation had constant coefficients, and so the authors see adiabatic variation introduces new dynamics into the nonlinear evolution of edge modes.
The authors note that since no pure edge mode exists for any range of frequencies ω in Case (III), this case will be omitted in the following discussion of pure edge modes.
Quasi-edge modes do not exist in the rapidly varying case studied in [28], and so the authors have shown adiabatic variation of the pseudo-field allows for new dynamics even at the linear level.