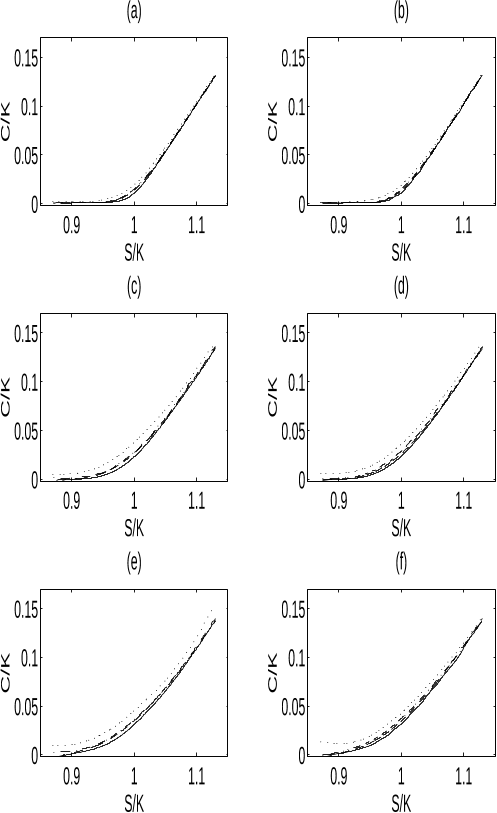
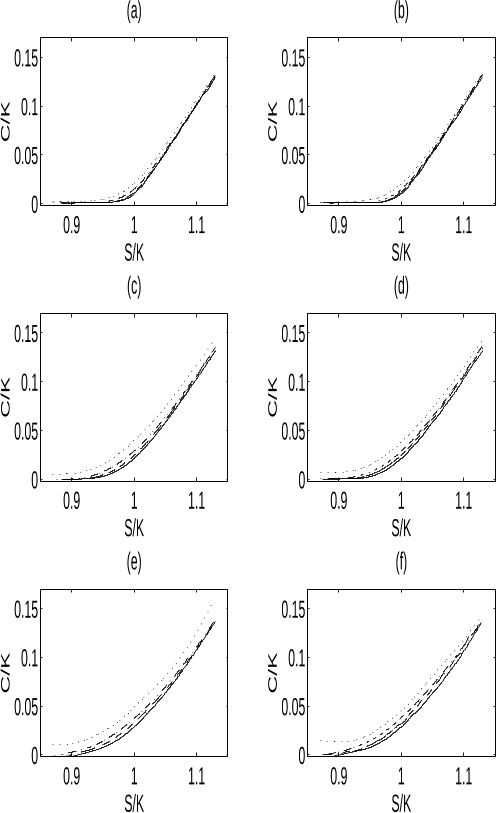
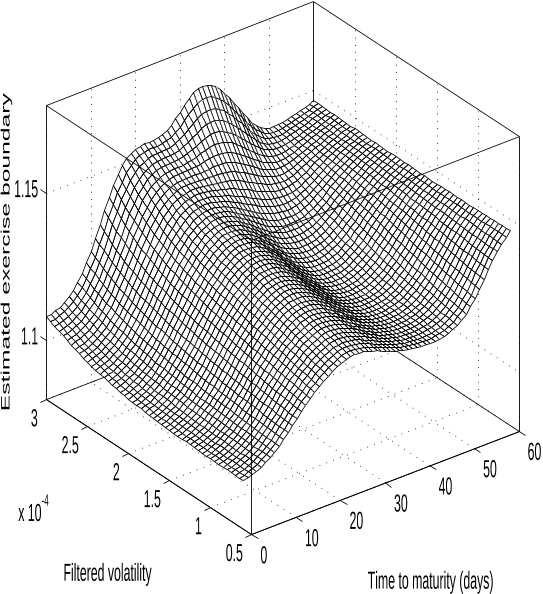
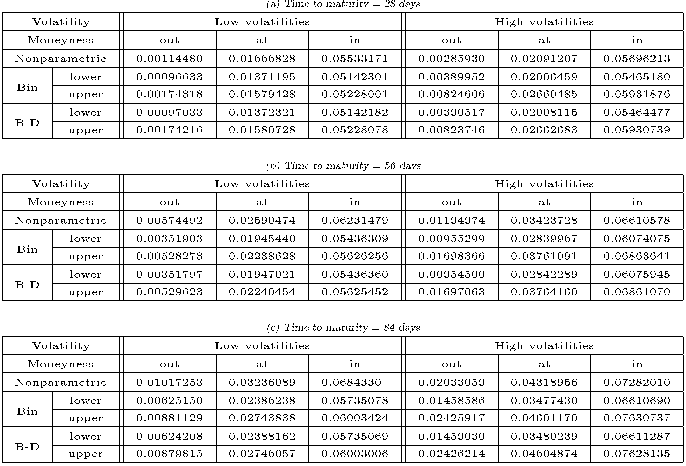
Abstract: 1 Martingales, Stopping Times, and Filtrations.- 1.1. Stochastic Processes and ?-Fields.- 1.2. Stopping Times.- 1.3. Continuous-Time Martingales.- A. Fundamental inequalities.- B. Convergence results.- C. The optional sampling theorem.- 1.4. The Doob-Meyer Decomposition.- 1.5. Continuous, Square-Integrable Martingales.- 1.6. Solutions to Selected Problems.- 1.7. Notes.- 2 Brownian Motion.- 2.1. Introduction.- 2.2. First Construction of Brownian Motion.- A. The consistency theorem.- B. The Kolmogorov-?entsov theorem.- 2.3. Second Construction of Brownian Motion.- 2.4. The SpaceC[0, ?), Weak Convergence, and Wiener Measure.- A. Weak convergence.- B. Tightness.- C. Convergence of finite-dimensional distributions.- D. The invariance principle and the Wiener measure.- 2.5. The Markov Property.- A. Brownian motion in several dimensions.- B. Markov processes and Markov families.- C. Equivalent formulations of the Markov property.- 2.6. The Strong Markov Property and the Reflection Principle.- A. The reflection principle.- B. Strong Markov processes and families.- C. The strong Markov property for Brownian motion.- 2.7. Brownian Filtrations.- A. Right-continuity of the augmented filtration for a strong Markov process.- B. A "universal" filtration.- C. The Blumenthal zero-one law.- 2.8. Computations Based on Passage Times.- A. Brownian motion and its running maximum.- B. Brownian motion on a half-line.- C. Brownian motion on a finite interval.- D. Distributions involving last exit times.- 2.9. The Brownian Sample Paths.- A. Elementary properties.- B. The zero set and the quadratic variation.- C. Local maxima and points of increase.- D. Nowhere differentiability.- E. Law of the iterated logarithm.- F. Modulus of continuity.- 2.10. Solutions to Selected Problems.- 2.11. Notes.- 3 Stochastic Integration.- 3.1. Introduction.- 3.2. Construction of the Stochastic Integral.- A. Simple processes and approximations.- B. Construction and elementary properties of the integral.- C. A characterization of the integral.- D. Integration with respect to continuous, local martingales.- 3.3. The Change-of-Variable Formula.- A. The Ito rule.- B. Martingale characterization of Brownian motion.- C. Bessel processes, questions of recurrence.- D. Martingale moment inequalities.- E. Supplementary exercises.- 3.4. Representations of Continuous Martingales in Terms of Brownian Motion.- A. Continuous local martingales as stochastic integrals with respect to Brownian motion.- B. Continuous local martingales as time-changed Brownian motions.- C. A theorem of F. B. Knight.- D. Brownian martingales as stochastic integrals.- E. Brownian functionals as stochastic integrals.- 3.5. The Girsanov Theorem.- A. The basic result.- B. Proof and ramifications.- C. Brownian motion with drift.- D. The Novikov condition.- 3.6. Local Time and a Generalized Ito Rule for Brownian Motion.- A. Definition of local time and the Tanaka formula.- B. The Trotter existence theorem.- C. Reflected Brownian motion and the Skorohod equation.- D. A generalized Ito rule for convex functions.- E. The Engelbert-Schmidt zero-one law.- 3.7. Local Time for Continuous Semimartingales.- 3.8. Solutions to Selected Problems.- 3.9. Notes.- 4 Brownian Motion and Partial Differential Equations.- 4.1. Introduction.- 4.2. Harmonic Functions and the Dirichlet Problem.- A. The mean-value property.- B. The Dirichlet problem.- C. Conditions for regularity.- D. Integral formulas of Poisson.- E. Supplementary exercises.- 4.3. The One-Dimensional Heat Equation.- A. The Tychonoff uniqueness theorem.- B. Nonnegative solutions of the heat equation.- C. Boundary crossing probabilities for Brownian motion.- D. Mixed initial/boundary value problems.- 4.4. The Formulas of Feynman and Kac.- A. The multidimensional formula.- B. The one-dimensional formula.- 4.5. Solutions to selected problems.- 4.6. Notes.- 5 Stochastic Differential Equations.- 5.1. Introduction.- 5.2. Strong Solutions.- A. Definitions.- B. The Ito theory.- C. Comparison results and other refinements.- D. Approximations of stochastic differential equations.- E. Supplementary exercises.- 5.3. Weak Solutions.- A. Two notions of uniqueness.- B. Weak solutions by means of the Girsanov theorem.- C. A digression on regular conditional probabilities.- D. Results of Yamada and Watanabe on weak and strong solutions.- 5.4. The Martingale Problem of Stroock and Varadhan.- A. Some fundamental martingales.- B. Weak solutions and martingale problems.- C. Well-posedness and the strong Markov property.- D. Questions of existence.- E. Questions of uniqueness.- F. Supplementary exercises.- 5.5. A Study of the One-Dimensional Case.- A. The method of time change.- B. The method of removal of drift.- C. Feller's test for explosions.- D. Supplementary exercises.- 5.6. Linear Equations.- A. Gauss-Markov processes.- B. Brownian bridge.- C. The general, one-dimensional, linear equation.- D. Supplementary exercises.- 5.7. Connections with Partial Differential Equations.- A. The Dirichlet problem.- B. The Cauchy problem and a Feynman-Kac representation.- C. Supplementary exercises.- 5.8. Applications to Economics.- A. Portfolio and consumption processes.- B. Option pricing.- C. Optimal consumption and investment (general theory).- D. Optimal consumption and investment (constant coefficients).- 5.9. Solutions to Selected Problems.- 5.10. Notes.- 6 P. Levy's Theory of Brownian Local Time.- 6.1. Introduction.- 6.2. Alternate Representations of Brownian Local Time.- A. The process of passage times.- B. Poisson random measures.- C. Subordinators.- D. The process of passage times revisited.- E. The excursion and downcrossing representations of local time.- 6.3. Two Independent Reflected Brownian Motions.- A. The positive and negative parts of a Brownian motion.- B. The first formula of D. Williams.- C. The joint density of (W(t), L(t), ? +(t)).- 6.4. Elastic Brownian Motion.- A. The Feynman-Kac formulas for elastic Brownian motion.- B. The Ray-Knight description of local time.- C. The second formula of D. Williams.- 6.5. An Application: Transition Probabilities of Brownian Motion with Two-Valued Drift.- 6.6. Solutions to Selected Problems.- 6.7. Notes.