



Did you find this useful? Give us your feedback









26 citations
20 citations
...In particular, the KdV equation is not only used to serve as a model to study surface water waves, acoustic-gravity waves in a compressible heavy fluid, axisymmetric waves in rubber cords, and hydromagnetic waves in a cold plasma, but also has been used recently to serve as a model to study blood pressure waves in large arteries [11–14, 30, 39]....
[...]
18 citations
13 citations
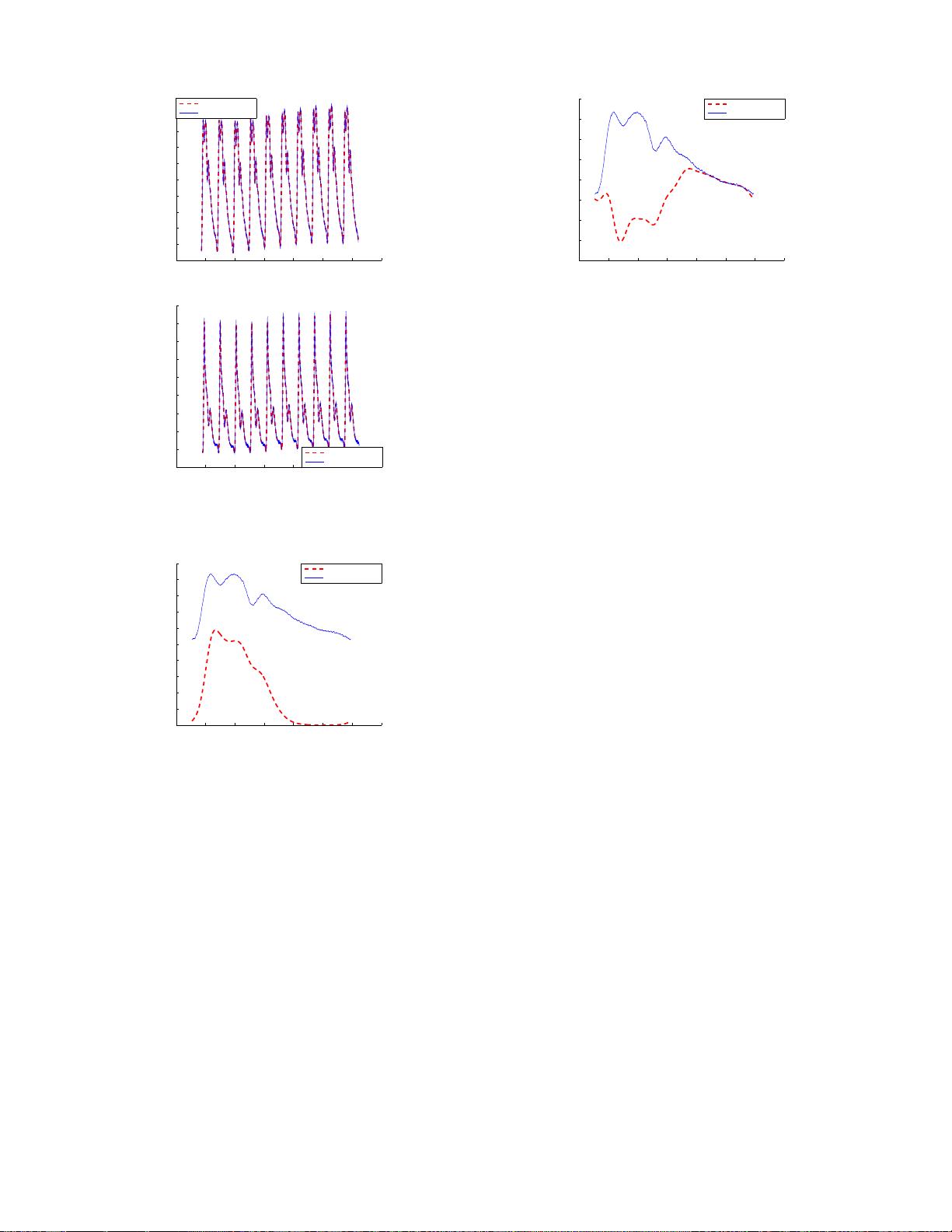
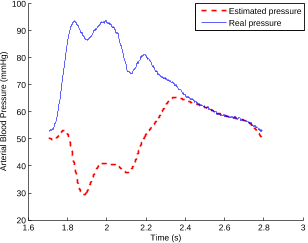
...We refer to [10], [11], [12] where for instance it is shown for λ = 0 how these quantities permit to discriminate between different pathological or physiological situations and also to provide some information on cardiovascular parameters of great interest....
[...]
...These quantities enable for example the discrimination between different pathological and physiological situations [12] and also provide information on some cardiovascular parameters of great interest as for example the stroke volume [11]....
[...]
19,846 citations
...The potential V is a well of variable depth which is determined by c. The number of the negative eigenvalues N(c) is a nondecreasing function of c and there is an infinite unbounded sequence of values of c at which N(c) is incremented by one, the new eigenvalue being born from the continuous spectrum [ 7 ], [10], [14]....
[...]
5,955 citations
3,461 citations
...This third order nonlinear partial derivative equation (NPDE) includes both nonlinear and dispersive effects and solitons result here from a stable equilibrium between these effects [20], [25]....
[...]
1,595 citations
The spectrum of this operator has two components : a continuous spectrum including positive eigenvalues and a discrete spectrum with negative eigenvalues [1], [4], [5], [6], [12].
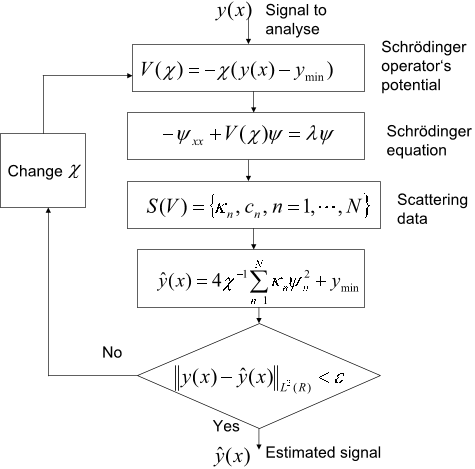
The main idea is then to find the parameter χ such that the signal y is well approximated by the reflectionless part of the potential which can be written then using equation (7) :ŷ = 4χ−1 N∑ n=1 κnψ2n + ymin, (9)where −κ2n and ψn, n = 1, · · · ,N are respectively the N negative eigenvalues and the corresponding L2-normalized eigenfunctions for the potential V , determined by the DST.
Denoting the positive eigenvalues by λ = k2, the continuous spectrum is characterized by the following asymptotic boundary conditions where T (k) and R(k) are respectively the transmission and the reflection coefficients associated to V :ψ(x,k)→ T (k)exp(−ikx), x→−∞, (2) ψ(x,k)→ exp(−ikx)+R(k)exp(ikx), x→+∞. (3)Conservation of energy leads to |T (k)|2 + |R(k)|2 = 1.
Determining the parameter χ determines the number N(χ) of negative eigenvalues and hence the number of solitons components required for a satisfying approximation of the signal y. Fig. 1 summarizes the SBSA method.
In this study the authors suppose that the function V belongs to the Schwartz space S (R) of regular and rapidly decreasing functions on R.The DST of the potential V is the solution of the spectral problem for L(V ).
This approach is based on the scattering transform and deals with the solution of the spectral problem of a perturbed Schrödinger operator for a given potential.