




Did you find this useful? Give us your feedback













3 citations
...We impose the same natural partial ordering on Ur as in [4]: first the singletons in lexicographic ordering, second the pairs in lexicographic ordering, then the triplets etc....
[...]
3 citations
1,290 citations
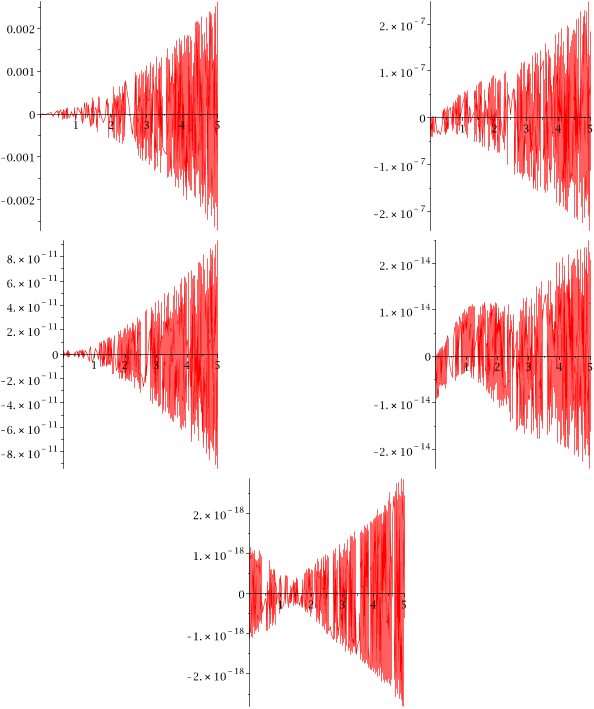
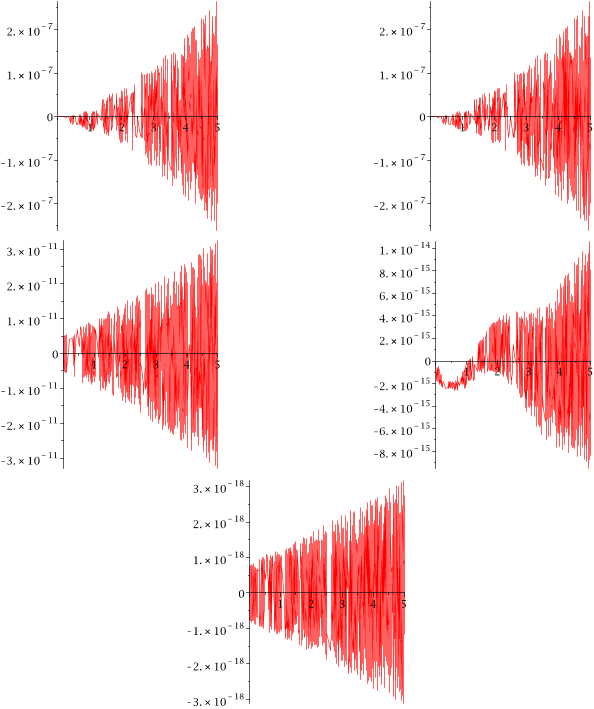
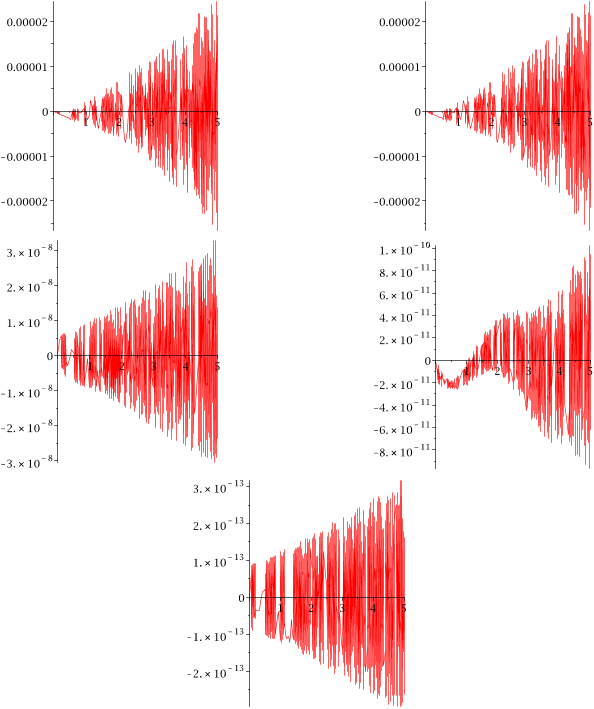
...Comment 1: As we increase levels r, we are increasingly likely to encounter the well-known phenomenon of small denominators (Verhulst 1990): unless κm = cψm, m = 1, · · · ,M , where all the ψms are rational (in which case, replacing ω by its product with the least common denominator of the ψms, we…...
[...]
...This is intended to prevent the occurrence of small denominators, familiar from asymptotic theory (Verhulst 1990)....
[...]
1,219 citations
...There is a measure of redundancy in the last expression: for example there are two terms in I2,3, namely (1,2) and (2,1), but they produce identical expressions....
[...]
...Since I1,2 = {2} and I2,2 = {(1, 1)}, we have from (3....
[...]
...Next to U3 = {0, 1, 2, 3, (1, 1), (1, 2), (1, 3), (2, 2), (2, 3), (3, 3)}, with σ1,1 = 2, σ1,2 = 1 + √ 2, σ1,3 = − √ 2, σ2,2 = 2 √ 2, σ2,3 = −1 and σ3,3 = −2− 2 √ 2....
[...]
...For example, in the case r = 3 we have I1,3 = {3}, I2,3 = {(1, 2)}, I3,3 = {(1, 1, 1)}, θ3 = θ1,1,1 = 1, θ1,2 = 2, while U3 = {0, 1, · · · ,M}∪{(m1,m2) : m1 ≤ m2, κm1+κm2 6= κm, ∀m = 0, · · · ,M}....
[...]
...…all the ψms are rational (in which case, replacing ω by its product with the least common denominator of the ψms, we are back to the case (1.2) of frequencies being integer multiples of ω) and positive, the set of all finite-length linear combinations of the κms is dense in R (Besicovitch 1932)....
[...]
810 citations
78 citations
...It is justified by important applications, not least in the modelling of nonlinear circuits (Giannini and Leuzzi 2004, Ramı́rez, Suárez, Lizarraga and Collantes 2010)....
[...]
72 citations