




Did you find this useful? Give us your feedback

















41 citations
28 citations
...Number of Modes Required for the 3MD Distribution In previous work, it has been reported that three modes are sufficient to accurately model amplitude distributions from spaceborne SAR data [17], airborne SETHI SAR data, and airborne INGARA real aperture sea clutter data [26]....
[...]
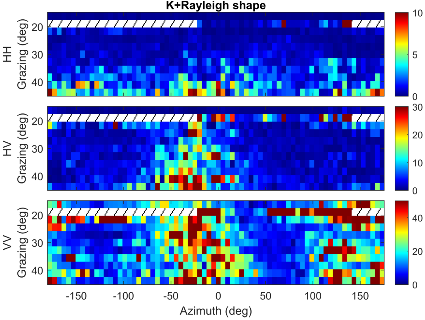
...Although not shown here, this result matches where the KR shape value is lowest indicating the spikiest clutter [26]....
[...]
...Among the 12 datasets (monostatic and bistatic), 7 need 2 or 3 modes (which is in agreement with [17] and [26]), but we find that 5 datasets need 4 or 5 modes....
[...]
...In previous work, it has been reported that three modes are sufficient to accurately model amplitude distributions from spaceborne SAR data [17], airborne SETHI SAR data, and airborne INGARA real aperture sea clutter data [26]....
[...]
...Among the 12 datasets (monostatic and bistatic), 7 need 2 or 3 modes (which is in agreement with [17,26]), but we find that 5 datasets need 4 or 5 modes....
[...]
8 citations
...Since then, 3MD has been successfully applied to a very diverse set of airborne and space-based radar data and SAR imagery in different frequency bands and polarizations as well as EO/IR data, see [51]–[53]....
[...]
6 citations
...The parameters may be estimated with a nonlinear LS fit to the data CCDF [9], [10], [19]....
[...]
...Rosenberg and Angelliaume [9] applied the 3MD model to sea clutter data from real and synthetic aperture radars, finding that the model was able to represent the clutter statistics well in all cases....
[...]
...In [9] and [10], the 3MD parameters were estimated with a nonlinear LS fit of the CCDF to the data....
[...]
1 citations
...3MD Distribution: Number of Modes It has previously been reported that I=3 modes are sufficient to accurately model amplitude distributions of high spatial resolution sea clutter data collected by spaceborne SAR sensors [10] as well as airborne RAR and SAR instruments [11]....
[...]
...This paper builds on that work by studying the same NetRAD monostatic and bistatic dataset with two newer proposed sea clutter distributions from the literature: the K+Rayleigh [9] and the tri-modal (3MD) distributions [10]-[11]....
[...]
...Among the 12 datasets (monostatic and bistatic), 7 need 2 or 3 modes (which is in agreement with [10] and [11]) but we find that 5 datasets need 4 or 5 modes....
[...]
606 citations
...The K+noise distribution has also been extended to a K+Rayleigh [8] distribution by taking into account any extra Rayleigh scattering not captured by the thermal noise....
[...]
...Compound distribution models include the K or K+noise [2], KA [2], KK [3], Pareto or Pareto+noise [4]–[7] and the K+Rayleigh [8]....
[...]
...The most commonly used PDF model for sea-clutter in both real and synthetic aperture radar is the K-distribution, or K+noise when thermal noise is included....
[...]
401 citations
202 citations
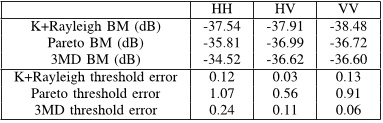
...However, the threshold errors which focus on the distribution tail, reveal that the K+Rayleigh and Pareto+noise models have a similar fitting error, while the 3MD model is significantly lower....
[...]
...The BD results focus on the overall fit and show that the K+Rayleigh model is slightly worse than the Pareto+noise and 3MD models....
[...]
...K+Rayleigh, magenta - Pareto+noise, black - 3MD. IV....
[...]
...When focusing on the tail of the distribution, low threshold errors are observed for both the K+Rayleigh and 3MD distributions, while the Pareto+noise model has a greater mismatch....
[...]
...[4] and later by others at US Naval Research Laboratory (NRL) and DST Group [5]–[7]....
[...]
118 citations
116 citations
...It was first used for seaclutter modelling by Balleri et al. [4] and later by others at US Naval Research Laboratory (NRL) and DST Group [5]–[7]....
[...]
...[4] and later by others at US Naval Research Laboratory (NRL) and DST Group [5]–[7]....
[...]
...In this paper, the 3MD model has been explored using data from the DST Group Ingara radar and the ONERA SETHI SAR....
[...]
...A. Ingara real beam data Ingara is a polarimetric radar system maintained and operated within the DST Group in Australia [14]....
[...]
One of the consequences of this discretisation is that spatial and longtime correlation cannot be modelled as part of the texture, and hence the model is less suitable for clutter simulation.
The most commonly used PDF model for sea-clutter in both real and synthetic aperture radar is the K-distribution, or K+noise when thermal noise is included.
For the Pareto distribution, the texture has an inverse gamma distributionP (x) = caΓ(a) x−a−1 exp [−c/x] , a > 1, c > 0 (4)where a is the shape and c = σ2c (a− 1) is the scale.
For a frequency agile or scanning radar with sufficient time between looks, a common method to improve the detection performance is to sum a number of looks.
To include the texture component which modulates the speckle, the authors integrate over the speckle mean power,P (z) = ∫ ∞ 0 P (z|x)P (x)dx (2)where P (x) is the distribution of the texture component.
During the ocean backscatter collections in 2004 and 2006, it was operated at X-band in a circular spotlight-mode where the aircraft flew a circular orbit in an anti-clockwise direction (as seen from above) around a nominated point of interest.
The K+Rayleigh model uses a gamma distribution for the texture,P (xr|νr, br) = bνrrΓ(νr) xνr−1r exp [−brxr] , 0 ≤ xr ≤ ∞ (3)where νr is the shape and br = νr/σ2c is the scale with the mean clutter power, σ2c .
It was first used for seaclutter modelling by Balleri et al. [4] and later by others atUS Naval Research Laboratory (NRL) and DST Group [5]–[7].
To calculate the compound distribution in (2), the integration is then performed with the modified speckle mean level, xr instead of the total speckle x.
Similarly to the K+Rayleigh model, the distribution parameters can be estimated using method of moments, the 〈z log z〉 method or least squares minimisation.
The compound models in the literature all assume a continuous texture distribution function which suggests a small probability of infinite texture values.
The SAR imagery has range resolutions of 0.5 m and 1.0 m for the X and L-bands respectively, and the imaged area is processed with an azimuth (alongtrack) resolution equal to the range resolution.
The K+Rayleigh, Pareto+noise and 3MD models have been fitted to the data with the model parameters shown in Tables III and IV for the X-band and L-band data sets.
The Pareto model is described by only two parameters (shape and scale), yet can reasonably model the long tails present in sea-clutter distributions.
Similarly to the Ingara data analysis, the authors observe that the third mode is required less for the VV polarisation, while the HH and HV polarisations nearly always require 3 modes, which is not the case for the Ingara dataset.