IEEE TRANSACTIONS ON WIRELESS COMMUNICATIONS, VOL. 8, NO. 6, JUNE 2009 2755
Co-ordinate Interleaved Spatial Multiplexing with
Channel State Information
K. V. Srinivas, Student Member, IEEE, R. D. Koilpillai, Member, IEEE, Srikrishna Bhashyam, Member, IEEE,
and K. Giridhar, Member, IEEE
Abstract—Performance of spatial multiplexing multiple-input
multiple-output (MIMO) wireless systems can be improved with
channel state information (CSI) at both ends of the link. This
paper proposes a new linear diagonal MIMO transceiver, re-
ferred to as co-ordinate interleaved spatial multiplexing (CISM).
With CSI at transmitter and receiver, CISM diagonalizes the
MIMO channel and interleaves the co-ordinates of the input
symbols (from rotated QAM constellations) transmitted over
different eigenmodes. The analytical and simulation results show
that with co-ordinate interleaving across two eigenmodes, the
diversity gain of the data stream transmitted ov er the weaker
eigenmode becomes equal to that of the data transmitted on the
stronger eigenmode, resulting in a significant improvement in the
overall diversity. The diversity-multiplexing tradeoff (DMT) is
analyzed for CISM and is shown that it achieves higher diversity
gain at all positive multiplexing gains compared to existing
diagonal transceivers. Over rank n MIMO channels, with input
symbols from rotated n-dimensional constellations, the DMT of
CISM is a straight line connecting the endpoints (0,N
t
N
r
) and
(min{N
t
,N
r
}, 0),whereN
t
and N
r
are the number of transmit
and recei ve antennas, respectively.
Index Terms—MIMO, spatial multiplexing, diversity,
beamforming, co-ordinate interleaving, precoding, diversity-
multiplexing gain tradeoff.
I. INTRODUCTION
M
ULTIPLE-INPUT multiple-output (MIMO) wireless
systems employing multiple antennas at each end have
the potential to improve data throughput over time varying
fading channels [1]. In rich scattering environments, MIMO
channels provide multiple paths for data transmission and offer
multiple degrees of freedom to communicate [2] . Multiple
paths can be exploited to obtain diversity gain by transmitting
the same symbol over all th e paths, and multiple degrees of
freedom can be used to increase the data rate through spatial
multiplexing [3].
Early spatial m ultiplexing systems were developed assum-
ing channel state information (CSI) only at the receiver. With
CSI at both ends, the transmit and receive algorithms can be
jointly designed to pre-process the data in a channel-dependent
way such that the system performance is further improved.
This is commonly known as transceiver design/optimization
Manuscript received April 19, 2005; revised January 11, 2007; accepted
October 23, 2008. The associate editor coordinating the review of this letter
and approving it for publication was X.-G. Xia.
The authors are with the Department of Electrical Engineering, Indian
Institute of Technology Madras, Chennai, india, 600036 (e-mail: {kvsri,
koilpillai, skrishna, giri}@tenet.res.in).
This work was financially supported by Centre of Excellence in Wireless
Technology (CEWiT), Chennai, India.
Part of this work was presented at IEEE Intl. Conf. Acoustics, Speech, and
Signal Processing, (ICASSP) 2006, Toulouse, France.
Digital Object Identifier 10.1109/TWC.2009.071391
and many emerging wireless standards are actively considering
such concepts.
Several optimality criteria have been used fo r designing
MIMO transceivers with CSI at both ends. Some of them
include, minimizing the sum of the mean square error (MSE)
of all data streams under an average power constraint [4],
minimizing the weighted sum of MSEs [5], minimizing the
product of MSEs with a peak power constraint [6] and
maximizing the minimum Euclidean distance between the
received signal points [ 7]. All these linear transceivers diago-
nalize the MIMO channel as it simplifies the solution through
scalarization. Optimality of diagonal MIMO structures has
been investigated in [8], where the authors have proposed a
unified framework for designing diagonal MIMO transceivers
according to a variety of optimality criterion including mini-
mizing the average (or, overall) error probability. The uniform
channel decomposition (UCD) scheme of [9], refer red as
UCD-VBLAST, is a non-linear transceiver that decomposes
the MIMO channel into mu ltiple identical sub-channels and
equalizes the MSEs of all the data streams.
Diagonalizing the MIMO channel through singular value
decomposition (SVD) and transmitting multiple data streams
over the resulting parallel eigen sub-channels or eigenmodes,
is a well known and simple linear diagonal MIMO transceiver.
It is referred to as SVD transceiver (SVDTR) in rest of the
paper. The overall error rate performance of SVDTR, as well
as the more advanced diagonal transceivers such as those
proposed in [8], is degraded by the lower diversity gains of
weaker eigenmodes [10]. Most o f the sophisticated diagonal
transceivers proposed in the literature improve coding gain
(compared to SVDTR) but not the diversity gain. Often, to
improve the diversity gain, data is transmitted only on the
stronger eigenmodes but this would render the remaining
degrees of freedom un-used.
In this paper, we propose a new linear diagonal transceiver,
referred to as co-ordinate interleaved spatial mu ltiplexing
(CISM) that improves the diversity gain of weaker eigen-
modes. CISM diagonalizes the MIMO channel through SVD
and interleaves the co-ordinates of the symbols (chosen from
rotated QAM constellations) transmitted over stro ng and weak
eigenmodes. Analytical results presented in the paper show
that co-ordinate interleaving across eigenmodes k and l,hav-
ing diversity gains g
d
(k) and g
d
(l), respectively, results in a di-
versity gain of max{g
d
(k),g
d
(l)} on both the channels. Thus,
CISM significantly improves overall error rate performance
without necessarily leaving out the weak eigenmodes. Further,
the diversity-multiplexing tradeoff is analyzed for CISM to
show that it achieves higher diversity gain at all multiplexing
1536-1276/09$25.00
c
2009 IEEE
Authorized licensed use limited to: INDIAN INSTITUTE OF TECHNOLOGY MADRAS. Downloaded on July 17, 2009 at 02:07 from IEEE Xplore. Restrictions apply.
2756 IEEE TRANSACTIONS ON WIRELESS COMMUNICATIONS, VOL. 8, NO. 6, JUNE 2009
gains compared to existing diagonal transceivers.
Notation: Bold upper case and lower case letters denote
matrices and vectors, respectively. a
kl
denotes (k, l)
th
entry
of matrix A and b
k
denotes k
th
element in vector b. x and
x are real and imaginary parts of x and :=
√
−1. I
N
, (·)
T
and (·)
H
denotes N × N identity matrix, transposition and
conjugate transposition, respectively. Pr{·},E[·] and ·
denote the pro bability of the event in brackets, expectation
and L
2
-norm of a vector, respectively. a indicates largest
integer less than or equal to a.
II. SYSTEM MODEL
Consider a N
t
× N
r
MIMO system with N
t
transmit and
N
r
receive antennas. The discrete time baseband input-output
relation of the MIMO channel is
y = Hs + n, (1)
where s ∈ C
N
t
×1
and y ∈ C
N
r
×1
are transmit and receive
symbol vectors, respectively, H ∈ C
N
r
×N
t
is the channel
matrix, and n ∈ C
N
r
×1
is the additive noise vector with
n
i
∼CN(0,σ
2
) and E[nn
H
]=σ
2
I
N
r
. The channel gains
{h
ij
} are assumed to be independent, frequency-flat Rayleigh
fading and hence, {h
ij
} are i.i.d with h
ij
∼CN(0, 1).We
define m := max{N
t
,N
r
},n:= min{N
t
,N
r
} and W :=
HH
H
when N
r
≤ N
t
and W := H
H
H when N
r
>N
t
,
and consider a slow-fading environment. For uncorrelated
Rayleigh MIMO channels, rank(H)=n =min{N
t
,N
r
}.
Let the SVD of H be H = UΛV
H
, where U ∈ C
N
r
×N
r
and V ∈ C
N
t
×N
t
are unitary matrices, and Λ ∈ R
N
r
×N
t
is a
diagonal matrix with
√
λ
k
∈ R
+
,thek
th
largest singular value
of H, as its k
th
diagonal element [11]. Let x ∈ C
K×1
,K≤
n, be the symbol vector with x
k
∈X
k
, 1 ≤ k ≤ K,whereX
k
is a unit energy QAM signal set employed on the k
th
eigen
sub-channel, and E[xx
H
]=I
K
. By transmitting s = V
K
Px,
where V
K
contains the first K columns of V, and by pre-
multiplying the received vector y with U
H
K
,weget
r = Λ
K
Px + w (2)
where r = U
H
K
y, w = U
H
K
n and Λ
K
= diag
{
√
λ
k
}
K
k=1
.
P = diag
{
√
p
k
}
K
k=1
where p
k
≥ 0 is the power allocated
to the k
th
data stream. The transmit power is constrained such
that
K
k=1
p
k
≤ P ,andSNR := P/σ
2
is the average SNR at
each receive antenna.
K denotes the number of active eigenmodes or eigen sub-
channels and the transmission scheme discussed above is
referred to as SVD transceiver (SVDTR) in rest of the paper.
It is also called multiple beamforming [12], and maximum
eigenmode beamforming (MEBF) corresponds to K =1.
A. Performance Measures: Diversity gain and Diversity-
Multiplexing Tradeoff
At high SNR, the average symbol error probability (SEP),
denoted by P
s
, can be approximated as P
s
≈ (g
c
SNR)
−g
d
,
where g
c
is the coding gain and g
d
is referred to as the
diversity gain [13]. The diversity gain g
d
(k) of k
th
eigen sub-
channel has been determined in [10] as
g
d
(k)=(m − k +1)(n − k +1),k=1,...,n (3)
and was also shown that g
d
(k) does not improve with spatial
power allocation. With K active eigenmodes, the overall
diversity gain of SVDTR is g
d
=min
k=1,...,K
{g
d
(k)}. Diversity
gains of most of the advanced diagonal transceivers are same
as that of SVDTR [10].
The diversity-m ultiplexing tradeoff (DMT) [2] is a mor e
fundamental performance measure o f a MIMO transceiver
in slow-fading scenario as it captures diversity gain and
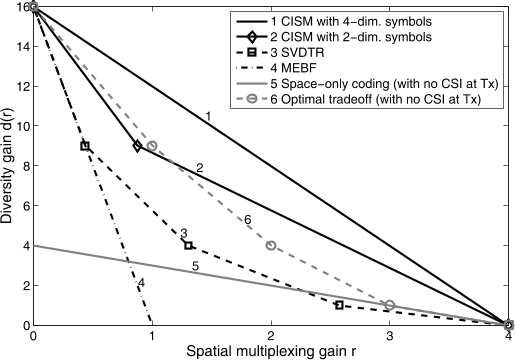
multiplexing gain. A diversity gain d(r) is achieved at a
multiplexing gain r, if the data rate scales as R = r log SNR
b/s/Hz and the SEP is
P
s
(r log SNR)
.
= SNR
−d(r)
(4)
where
.
= denotes exponential equality [2]. Note that g
d
is the
diversity gain for fixed input data rate (i.e., g
d
= d(0)), and
to distiguish from d(r), it is referred to as classical diversity
gain [14] wherever necessary. The DMT for SVDTR has been
evaluated in [12]. We derive the DMT of CISM in section V.
III. C
O-ORDINATE INTERLEAVED SPATIAL MULTIPLEXING
In this sectio n, co-ordinate interleaved spatial multiplexing
(CISM) is described. The proposed scheme is based on co-
ordinate interleaving (CI), a technique which was originally
proposed to exploit the co-ordinate,or,component level di-
versity for single antenna transmission over Rayleigh fading
channels [15], [16]. The idea is to interleave the real an d
imaginary parts of the complex symbols at the transmitter
such that they go through independently fading channels. For
CI to be effective, no two signal points in the signal set X
should have the same co-ordinate. This condition can be met
by rotating the standard M -QAM signal sets [15], [16]. In
the following, we assume that the signal sets {X
k
}
K
k=1
are
appropriately rotated. The effect of rotation angle and the
optimal angle of rotation are discussed in subsequent sections.
A. CISM Transceiver
• Interleave real and imaginary parts of {x
k
}
K
k=1
(K ≤ n)
to obtain {˜x
k
}
K
k=1
,where,
˜x
k
= x
k
+ x
K−(k−1)
(5)
• Transmit s = V
K
P˜x,where˜x =[˜x
1
˜x
2
...˜x
K
]
T
•
Receive ˜y = Hs + n = HV
K
P˜x + n
• Obtain ˜r = U
H
K
˜y = Λ
K
P˜x + w,whereΛ
K
=
diag
{
√
λ
k
}
K
k=1
and w = U
H
K
n.
⇒ ˜r
k
=
λ
k
p
k
˜x
k
+ w
k
,k=1,...,K
• De-interleave ˜r
k
to obtain r
k
:
r
k
= ˜r
k
+ ˜r
K−(k−1)
,k=1,...,K (6)
⇒ r
k
=
λ
k
p
k
x
k
+
λ
K−(k−1)
p
K−(k−1)
x
k
+ w
k
+ w
K−(k−1)
(7)
• Estimate x
k
,k=1,...,K :
ˆx
k
=arg min
x
k
∈X
k
r
k
−
λ
k
p
k
x
k
+
λ
K−(k−1)
p
K−(k−1)
x
k
2
(8)
Authorized licensed use limited to: INDIAN INSTITUTE OF TECHNOLOGY MADRAS. Downloaded on July 17, 2009 at 02:07 from IEEE Xplore. Restrictions apply.
IEEE TRANSACTIONS ON WIRELESS COMMUNICATIONS, VOL. 8, NO. 6, JUNE 2009 2757
As can be seen from (7), the received signals gets decoupled
and hence can be decoded by single-symbol maximum likeli-
hood (ML) decoding. It is easy to verify that the received
signal power on the interleaved k
th
and (K − (k − 1))
th
eigenmodes is the same and hence, X
k
and X
K−(k−1)
are
assumed to be the same. Among the K eigenmodes used
for transmission, the two symbols transmitted on strongest
and weakest eigenmodes are interleaved and the two sym-
bols transmitted on second strongest and second weakest
eigenmodes are interleaved and so on. When K is an odd
number, symbols transmitted on
K+1
2
th
eigenmode will not
get affected by the interleaving.
IV. D
IVERSITY GAIN OF CISM
The error rate performance of CISM, in particular, the
diversity gain, is analyzed in this section. We consider uncoded
transmission over K ≤ n eigenmodes with
1
p
k
= P/K, k =
1,...,K, and assume X
k
= X
K−(k−1)
. MIMO channels
with rank(H)=2are considered in the foolowing and
rank(H) > 2 case is deferred to section V.
A. MIMO Channels with rank(H)=2
Consider H ∈ C
N
r
×N
t
with n =min{N
t
,N
r
} =2.When
{h
ij
} are i.i.d and h
ij
∼CN(0, 1),rank(H)=n =2with
probability one. For illustrative purpose, we consider 4-QAM
signaling and analysis for any M-QAM can be done in a
similar way.
Let X
1
= X
2
= X = {x
A
,x
B
,x
C
,x
D
} where x
A
=
e
jθ
(
1
2
+
1
2
),x
B
= e
jθ
(−
1
2
+
1
2
),x
C
= −x
A
and x
D
= −x
B
.
Let P
4-QAM
s,k
denote the SEP on k
th
eigenmode and P
4-QAM
s
be
the average SEP, averaged over both the eigenmodes.
Result 1: P
4-QAM
s,1
= P
4-QAM
s,2
= P
4-QAM
s
and
P
4-QAM
s
≤ Pr{x
A
→ x
B
} + Pr{x
A
→ x
C
} + Pr{x
A
→ x
D
}
(9)
where
Pr{x
A
→ x
B
} = Pr{x
A
→ x
D
} =
m
2π
π
2
0
1
(1 +
SNR
8sin
2
t
cos
2
θ)
m+1
(1 +
SNR
8sin
2
t
sin
2
θ)
m−1
dt
+
m
2π
π
2
0
1
(1 +
SNR
8sin
2
t
cos
2
θ)
m−1
(1 +
SNR
8sin
2
t
sin
2
θ)
m+1
dt
−
m − 1
π
π
2
0
1
(1 +
SNR
8sin
2
t
cos
2
θ)
m
(1 +
SNR
8sin
2
t
sin
2
θ)
m
dt
(10)
and
Pr{x
A
→ x
C
} =
m
2π
π
2
0
1
(1 +
SNR
8sin
2
t
ψ
1
)
m+1
(1 +
SNR
8sin
2
t
ψ
2
)
m−1
dt
+
m
2π
π
2
0
1
(1 +
SNR
8sin
2
t
ψ
1
)
m−1
(1 +
SNR
8sin
2
t
ψ
2
)
m+1
dt
−
m − 1
π
π
2
0
1
(1 +
SNR
8sin
2
t
ψ
1
)
m
(1 +
SNR
8sin
2
t
ψ
2
)
m
dt (11)
1
As power allocation effects only the coding gain but not the diversity
gain [10], we consider uniform power allocation.
where ψ
1
=1−sin 2θ and ψ
2
=1+sin2θ.
Proof: See Appendix A.
At high SNR, assuming sin 2θ =0and |sin 2θ| =1,
the pairwise error probabilities (PEPs) given above can be
approximated as follows.
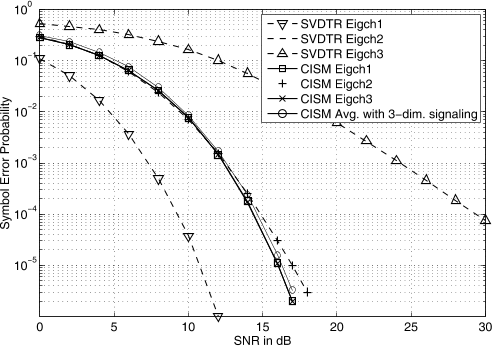
Pr{x
A
→ x
B
}≈κC
AB
SNR
−2m
(12)
where κ =
8
2m
m
4
4m−1
4m
4m−3
4m−2
···
1
2
and
C
AB
=
1
(cos
2
θ)
m+1
(sin
2
θ)
m−1
+
1
(cos
2
θ)
m−1
(sin
2
θ)
m+1
−
2(m − 1)
m
1
(cos
2
θ sin
2
θ)
m
(13)
Similarly,
Pr{x
A
→ x
C
}≈κC
AD
SNR
−2m
(14)
where
C
AD
=
1
ψ
m+1
1
ψ
m−1
2
+
1
ψ
m−1
1
ψ
m+1
2
−
2(m − 1)
m
1
(ψ
1
ψ
2
)
m
(15)
Hence, at high SNRs,
P
4-QAM
s
≤ κ(2C
AB
+ C
AD
)SNR
−2m
(16)
θ
opt
, the optimal rotation angle, is computed by maximizing
the coding gain (2C
AB
+ C
AD
). For example, when m =2,
θ
opt
=27.9
o
and for m =4, θ
opt
=29.15
o
.
P
s,1
is lower bounded by the PEP corresponding to confus-
ing x
A
with its nearest n eighbor.
Pr{x
A
→ x
B
} <P
4-QAM
s,1
≤
Union bound on P
4-QAM
s,1
From (12) and (14), we see that,
κC
AB
SNR
−2m
<P
4-QAM
s,1
≤ κ (C
AB
+ C
AC
+ C
AD
) SNR
−2m
As both the upper bound and lower bound on P
4-QAM
s,1
have the
same SNR exponent, it follows that data transmitted on first
eigenmode has a diversity gain of 2m. By a similar argument,
we can show that P
4-QAM
s,2
decays as SNR
−2m
and hence
the overall diversity gain is 2m. SEP analysis for any M-
QAM can be carried out in a similar way to show that CISM
always achieves the maximum diversity gain 2m offered by
the channel when rank(H)=2.
When the input symbols are from rotated BPSK, i.e., when
X
1
= X
2
= X = {e
θ
, −e
θ
}, we compute exact SEP without
resorting to union bound and is given below.
P
BPSK
s,1
= P
BPSK
s,2
= P
BPSK
s
=
m
2π
π
2
0
1
(1 +
SNR
4sin
2
t
cos
2
θ)
m+1
(1 +
SNR
4sin
2
t
sin
2
θ)
m−1
dt
+
m
2!π
π
2
0
1
(1 +
SNR
4sin
2
t
cos
2
θ)
m−1
(1 +
SNR
4sin
2
t
sin
2
θ)
m+1
dt
−
m − 1
π
π
2
0
1
(1 +
SNR
4sin
2
t
cos
2
θ)
m
(1 +
SNR
4sin
2
t
sin
2
θ)
m
dt
(17)
Numerical evaluation of θ
opt
results in θ
opt
=45
o
, ∀m ∈ N.
Authorized licensed use limited to: INDIAN INSTITUTE OF TECHNOLOGY MADRAS. Downloaded on July 17, 2009 at 02:07 from IEEE Xplore. Restrictions apply.
2758 IEEE TRANSACTIONS ON WIRELESS COMMUNICATIONS, VOL. 8, NO. 6, JUNE 2009
V. D IVERSITY-MULTIPLEXING TRADEOFF OF CISM
In the following, we compute the SEP P
s,k
when R
k
,data
rate on k
th
eigenmode, scales with SNR as R
k
= r
k
log SNR
b/s/Hz, r
k
∈ [0, 1], and obtain the DMT o f CISM.
Result 2: The sy mbol error prob a bility of k
th
eigenmode at
a multiplexing gain of r is given by
P
s,k
.
= SNR
−g
CISM
d
(k)(1−r
k
)
r
k
∈ [0, 1] (18)
where
g
CISM
d
(k)=max{g
d
(k),g
d
(K − (k − 1))} (19)
and g
d
(k)=(m −k +1)(n − k +1).
Proof: See Appendix B.
The classical diversity gain of k
th
data stream can be obtained
by making r
k
=0in (18).
Remark 1: The (classical) diversity gain of k
th
data stream
in CISM is given by
g
CISM
d
(k)=(m − i +1)(n − i +1),k=1,...,K (20)
where i =min{k, K −(k −1)}. It follows from (3) and (19).
Note that g
CISM
d
(k)=g
CISM
d
(K − (k − 1)). Letting n =2and
K =2, it can be noticed that remark 1 is consistent with
the results obtained in section IV. Remark 1 shows that, co-
ordinate interleaving two data streams transmitted over two
eigenmodes having different diversity gains would make the
diversity gain of both the streams equal to the diversity gain of
stronger eigenmode. Thus, CISM improves the diversity gains
of the weaker eigenmodes resulting in a significant gain in the
overall diversity, as shown by the following remark.
Remark 2: The overall (classical) diversity gain of CISM
with K ≤ n is given by
g
CISM
d
=
m −
K +1
2
+1
n −
K +1
2
+1
(21)
SVDTR, as well as many advanced diagonal transceivers such
as those proposed in [8], have an overall diversity gain of g
d
=
(m−K +1)(n−K+1)[10]. Hence, for any choice of K, 1 <
K ≤ n, CISM results in a significantly higher diversity gain
than existing diagonal transceivers. When K =1, both CISM
and SVDTR reduces to MEBF. Now, we proceed to determine
the DMT achieved b y CISM.
When K = n =2, P
s,1
.
= SNR
−2m(1−r
1
)
and P
s,2
.
=
SNR
−2m(1−r
2
)
. Dividing the total input data rate R =
r log SNR,r∈ [0, 2], equally between the two eigenmodes
results in the following.
Remark 3:Overrank2 MIMO channels, CISM achieves
the DMT given b y,
d
CISM
(r)=2m(1 − r/2),r∈ [0, 2] (22)
Fig. 1 shows the DMT for 4 × 2 MIMO channel. The
tradeoff for SVDTR (or, mu ltiple beamforming), and MEBF
are derived in [12]. The figur e also shows the optimal tradeoff
of the MIMO channel with coding across space and time
(“Optimal tradeoff”) and “space-only coding” without CSI at
the transmitter, derived in [2]. The UCD-VBLAST transceiver
achieves the optimal open-loop tradeoff [9] and hence, the
“Optimal tradeoff” curve also shows the DMT of UCD-
VBLAST. Note that CISM is space-only coding with CSI at
the transmitter.
012
0
1
2
3
4
5
6
7
8
Spatial multiplexing gain r
Diversity gain d(r)
1 CISM
2 SVDTR
3 MEBF
4 Space−only coding (with no CSI at Tx)
5 Optimal tradeo (with no CSI at Tx)
1
2
3
4
5
Fig. 1. Diversity-Multiplexing tradeof f comparisons of different schemes
over 4 × 2 MIMO channel.
When n>2 and K>2, CISM results in un-equal
diversity gains {g
CISM
d
(k)}
K
k=1
and the overall diversity gain
is determined by min{g
CISM
d
(k)}
K
k=1
. With uniform rate allo-
cation (r
k
= r/K, k =1,...,K) across all the K active
eigenmodes,
d
CISM
(r)=g
CISM
d
(i)(1 − r/K),r∈ [0,K] (23)
where i =
K+1
2
and g
CISM
d
(i) is given by (20). The tradeoff
can be improved by finding the optimal number of active
eigenmodes (K
∗
) for each input rate r, and by optimally
distributing the rate across the active modes. We note that,
a similar analysis has been repor ted in [12] for multiple
beamforming. Define G
CISM
d
(2k − 1) := g
CISM
d
(k) for k =
1,...,
n+1
2
and G
CISM
d
(2k):=g
CISM
d
(k) for k =1,...,
n
2
and G
CISM
d
(n +1) := 0.LetD(K, r)=G
CISM
d
(1)(1 − r
1
)=
··· = G
CISM
d
(K)(1 − r
K
),K≤ n. We need to find K
∗
=
max
K
D(K, r) subject to the constraint
K
∗
k=1
r
k
= r.This
results in
K
∗
=argmax
K
D(K, r) = arg max
K
K − r
K
i=1
(1/G
CISM
d
(i))
(24)
with optim al rate allocatio n given by
r
k
=1−
D(K
∗
,r)
G
CISM
d
(k)
,k=1,...,K
∗
(25)
Connecting the points (r(k), d(k)),where
r(k)=
⎧
⎪
⎨
⎪
⎩
0 k =0
k − G
CISM
d
(k +1)
k
i=1
1/G
CISM
d
(i)
0 <k<n
nk= n
(26)
and
d(k)=G
CISM
d
(k +1) k =0,...,n (27)
gives the DMT curve. Transition points are obtained by
equating D(i, r(i)) = D(i +1, r(i)),i=1,...,n− 1.
Authorized licensed use limited to: INDIAN INSTITUTE OF TECHNOLOGY MADRAS. Downloaded on July 17, 2009 at 02:07 from IEEE Xplore. Restrictions apply.
IEEE TRANSACTIONS ON WIRELESS COMMUNICATIONS, VOL. 8, NO. 6, JUNE 2009 2759
0 1 2 3 4
0
2
4
6
8
10
12
14
16
Spatial multiplexing gain r
Diversity gain d(r)
1
2
3
4
5
6
1 CISM with 4−dim. symbols
2 CISM with 2−dim. symbols
3 SVDTR
4 MEBF
5 Space−only coding (with no CSI at Tx)
6 Optimal tradeoff (with no CSI at Tx)
Fig. 2. Dive rsity-Multiplexing tradeoff comparisons of different schemes
over 4 × 4 MIMO channel.
A. CISM with multi-dimensional signaling
Intrigued by (22), we investigate the DMT of CISM over
rank n MIMO channels when the input symbols are from
rotated n-dimensional QAM constellations. An n-dimensional
QAM signal set is obtained as the Cartesian product o f n/2
two-dimensional QAM signal sets [16]. To send b bits in
n-dimensions, the n-dimensional constellation will have (at
least) 2
b
points. A symbol vector from a rotated n-dimensional
constellation is denoted by x
k
= v
k
Φ,x
k
∈ R
n
,where,
v
k
=(v
k
(1),...,v
k
(n)) ∈ Z
n
is the un-rotated n-dimensional
QAM symbol and Φ is a rotation matrix chosen such that
x
k
(i) = x
l
(i), 1 ≤ k, l ≤ 2
b
,k = l.
To achieve an overall input data rate of R = r log SNR
b/s/Hz, r ∈ [0,n], we choose two n-dimensional symbols
(say, x
1
and x
2
) carrying R/2 bits each. The symbols are
interleaved to obtain ˜x ∈ C
n
where
˜x
i
= x
1
(i)+x
2
(i),i=1,...,n (28)
The received vector ˜r =ΛP˜x + w is de-interleaved to obtain
r
1
= ˜r and r
2
= ˜r where
r
i
(j)=
λ
j
p
j
x
i
(j)+w
j
,i=1, 2; j =1,...,n (29)
ˆx
i
are obtained from r
i
through single (n-dimensional) symbol
ML decoding.
Result 3: DMT achieved by CISM over rank n MIMO
channels with input symbols from rotated n-dimensional con-
stellations is given by
d(r)=mn
1 −
r
n
,r∈ [0,n] (30)
Proof: See Appendix C.
Fig. 2 compares DMT achieved by d ifferent schemes over
4 ×4 MIMO channel. DMT of CISM with 2-dimensional sig-
naling is p lotted according to (26) and (27) and it outperforms
SVDTR and MEBF. As shown by (30), DMT achieved by
CISM with 4-dimensional input symbols is a straight line
connecting the endpoints (0, 16) and (4, 0). Note that the
improved tradeoff with n-dimensional symbols is achieved at
the cost of higher decoding complexity.
0 2 4 6 8 10 12 14 16 18 20
10
−5
10
−4
10
−3
10
−2
10
−1
10
0
SNR in dB
Symbol Error Probability
SVDTR Eigch1
SVDTR Eigch2
SVDTR Avg
CISM Eigch1
CISM Eigch2
CISM Analytical
Fig. 3. Example 1: Symbol error probability of SVDTR and CISM
over 2 × 2 MIMO channel with BPSK signaling. Note that CISM Avg =
CISM Eigch1=CISM Eigch2.
Result 3 may b e interpreted as, in MIMO channels, it is
possible to achieve a linear DMT connecting the end points
(0,mn) and (n, 0) with space-only coding with perfect CSI
at both ends. CISM achieves this with appropriate signaling.
VI. S
IMULATION RESULTS
This section reports SEP of the proposed CISM transceiver,
evaluated through Monte Carlo simulations. We consider
block-fading channel and uncoded data transmission over
K = n eigenmodes with p
k
= P/n, k =1,...,nand P =1.
Example 1: For N
t
=2and N
r
=2,theSEPof
SVDTR and CISM is plotted in Fig. 3. Data symbols are
drawn from BPSK constellation rotated by θ
opt
=45
0
.
“SVDTR Eigchk” and “CISM Eigchk” refers to k
th
eigen sub-
channel of SVDTR and CISM, respectively. “SVDTR Avg”
and “CISM Avg” denote the overall SEP of SVDTR and
CISM, respectively. In SVDTR, as shown in [10], the second
eigenmode drastically degrades the overall SEP. In CISM,
both the eigenmodes have equal SEP with 4
th
order diversity.
Analytical SEP, plotted by evaluating (17) with m =2,
matches exactly with the simulation results.
Example 2: Consider CISM over 2 × 2 MIMO channel
with data symbo ls from 4-QAM constellation rotated by
θ
opt
=27.9
o
. Note that θ
opt
is different from 31.7175
o
which is
the optimal rotation angle when bo th the channels are Rayleigh
fading channels with unit diversity gain [17]. Fig. 4 compares
the SEP obtained through simulations with the union bound
given by (9). It also shows the SEP of UCD-VBLAST which
involves unitary precoding along with optimal power alloca-
tion [9]. Both UCD-VBLAST and CISM achieve maximum
diversity gain of 4 but CISM (with un iform power allocation)
has slightly lower coding gain. “CISM+PL” denotes CISM
with power a llocation given by p
k
=
2P
K
λ
k
λ
k
+λ
K−(k−1)
,k =
1,...,K. It can be verified that this power allocation r esults
in higher received SNR compared to uniform power allocation.
The power allocation given above is a heuristic one and
determining the optimal power allocation will be considered
in the future work. Further, since the DMT of UCD-VBLAST
Authorized licensed use limited to: INDIAN INSTITUTE OF TECHNOLOGY MADRAS. Downloaded on July 17, 2009 at 02:07 from IEEE Xplore. Restrictions apply.