
Appl. Phys. Lett. 113, 243703 (2018); https://doi.org/10.1063/1.5064363 113, 243703
© 2018 Author(s).
Controlling shedding characteristics of
condensate drops using electrowetting
Cite as: Appl. Phys. Lett. 113, 243703 (2018); https://doi.org/10.1063/1.5064363
Submitted: 03 October 2018 . Accepted: 24 November 2018 . Published Online: 11 December 2018
Ranabir Dey, Jander Gilbers, Davood Baratian , Harmen Hoek, Dirk van den Ende, and Frieder Mugele
COLLECTIONS
This paper was selected as an Editor’s Pick
ARTICLES YOU MAY BE INTERESTED IN
Self-propelling Leidenfrost droplets on a variable topography surface
Applied Physics Letters 113, 243704 (2018); https://doi.org/10.1063/1.5056249
Investigation of Gilbert damping of a tetragonally distorted ultrathin Fe
0.5
Co
0.5
epitaxial film
with high magnetic anisotropy
Applied Physics Letters 113, 232406 (2018); https://doi.org/10.1063/1.5052721
Propensity for spontaneous relaxor-ferroelectric transition in quenched (Na
1/2
Bi
1/2
)TiO
3
-
BaTiO
3
compositions
Applied Physics Letters 113, 252902 (2018); https://doi.org/10.1063/1.5053989

Controlling shedding characteristics of condensate drops using
electrowetting
Ranabir Dey, Jander Gilbers, Davood Baratian, Harmen Hoek, Dirk van den Ende,
and Frieder Mugele
a)
Physics of Complex Fluids, MESAþ Institute for Nanotechnology, University of Twente, PO Box 217,
7500 AE Enschede, The Netherlands
(Received 3 October 2018; accepted 24 November 2018; published online 11 December 2018)
We show here that ac electrowetting (ac-EW) with structured electrodes can be used to control the
gravity-driven shedding of drops condensing onto flat hydrophobic surfaces. Under ac-EW with
straight interdigitated electrodes, the condensate drops shed with relatively small radii due to the ac-
EW-induced reduction of contact angle hysteresis. The smaller shedding radius, coupled with the
enhanced growth due to coalescence under EW, results in an increased shedding rate. We also show
that the condensate droplet pattern under EW can be controlled, and the coalescence can be further
enhanced, using interdigitated electrodes with zigzag edges. Such enhanced coalescence in conjunc-
tion with the electrically induced trapping effect due to the electrode geometry results in a larger
shedding radius, but a lower shedding rate. However, the shedding characteristics can be further opti-
mized by applying the electrical voltage intermittently. We finally provide an estimate of the conden-
sate volume removed per unit time in order to highlight how it is enhanced using ac-EW-controlled
dropwise condensation. Published by AIP Publishing. https://doi.org/10.1063/1.5064363
Dropwise condensation is important in a wide range of
technologies like water-harvesting systems,
1
desalination sys-
tems,
2
and heat exchangers.
3
The effectiveness of all these
technologies depends on the efficient volumetric collection
rate of the condensate and, hence, depends on the shedding of
the condensate drops from the condensing surface. The con-
tinuous drop shedding exposes the bare surface for renewed
nucleation and growth of the condensate drops culminating in
efficient vapour-to-liquid phase changes and enhanced con-
densate collection.
4
To this end, the enhanced mobility and
shedding of condensate drops have been studied on superhy-
drophobic nanostructured surfaces,
5–8
wettability-patterned
surfaces,
9
liquid impregnated textured surfaces,
10,11
and bio-
mimetic surfaces.
12
All these approaches towards enhancing
droplet mobility are passive in nature, relying solely on the
topographical and/or chemical patterning of the condensing
surface. As an alternative, recently we have demonstrated that
an alternating (ac) electric field in an electrowetting (EW)
configuration with structured electrodes can be used to
actively control the mobility of condensate drops on homoge-
neous hydrophobic surfaces.
13
The growth of the condensate
drops under EW is characterized by their migration to the
size-dependent locations of the minima in the corresponding
electrostatic energy landscapes and by enhanced coales-
cence.
13
The use of electrical forces to control condensate
droplet pattern (breath figures) evolution is—to our knowl-
edge—a completely new approach. While in our previous
study, we focused on the evolution and statistics of the con-
densate droplet pattern, the present work is devoted to the
analysis of subsequent gravity-driven shedding of condensate
drops under ac-EW. Such a study is essential for the effective
implementation of EW for technological applications involv-
ing dropwise condensation.
In this letter, we demonstrate that the gravity-driven
shedding characteristics of condensate drops can be indeed
controlled using ac-EW with structured electrodes. In gen-
eral, a condensate drop on a vertical substrate begins to shed
under gravity only when the drop reaches a certain critical
“shedding” radius R
sh
at which its weight overcomes the
inherent contact angle hysteresis force.
14
It has also been
demonstrated that ac-EW in air results in the reduction of the
effective contact angle hyste resis culminating in enhanced
mobilization of sessile drops.
15,16
We show here that under
ac-EW with straight interdigitated electrodes, the underlying
reduction in effective contact angle hysteresis and the
enhanced coalescence result in smaller R
sh
and the increased
shedding rate ðf
sh
Þ of the condensate drops, as compared to
the classical no EW case. Interestingly, the shedding charac-
teristics under ac-EW can be further altered using interdigi-
tated electrodes with zigzag edges. In this case, the enhanced
mobility of condensate drops due to the non-uniform electri-
cal force distribution and the eventual electrical trapping
effect result in larger R
sh
and lower f
sh
; however, the overall
condensate removal rate increases. Finally, we demonstrate
that the condensate shedding is further enhanced by applying
the electrical voltage intermittently instead of continuously.
The experimental setup is identical to that used in our
previous study
13
(see Sec. S1 in the supplementary material
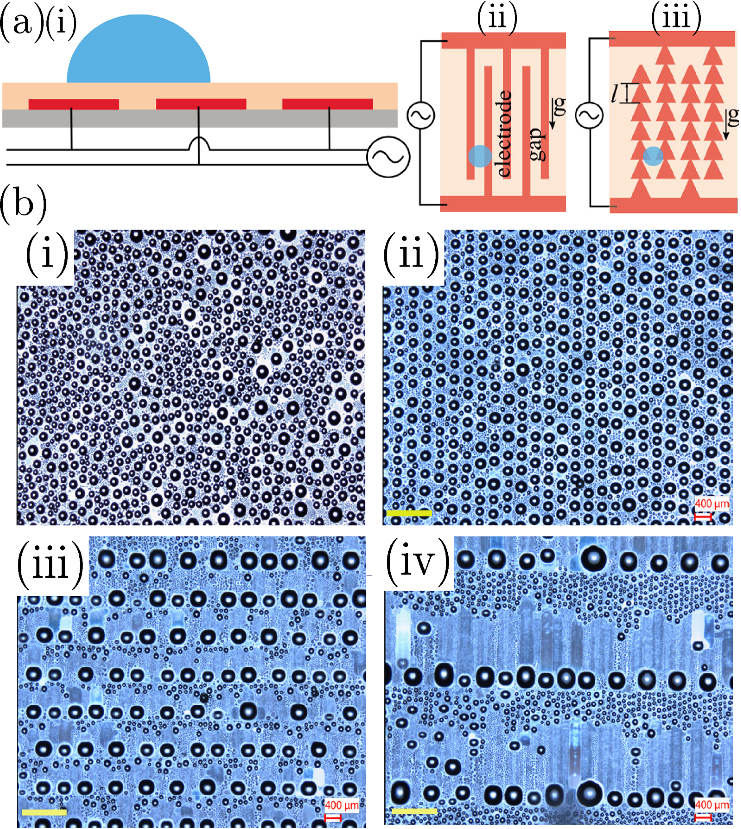
for a schematic). The condensing substrate [Fig. 1(a-i)] con-
sists of interdigitated ITO electrodes (red) on a glass sub-
strate (gray), which is coated with a hydroph obic dielectric
film (orange)—2 lm thick Parylene C layer topped with an
ultrathin layer of Cytop. For the straight interdigitated elec-
trodes [Fig. 1(a-ii)], the width of both the electrodes and the
gaps is 200 lm; for the zigzag interdigitated electrodes [Fig.
1(a-iii)], the base and the apex of each triangular element for
both electrodes and gaps are 250 lm and 50 lm wide, respec-
tively, while the distance l between the consecutive
a)
E-mail: f.mugele@utwente.nl
0003-6951/2018/113(24)/243703/5/$30.00 Published by AIP Publishing.113, 243703-1
APPLIED PHYSICS LETTERS 113, 243703 (2018)

triangular elements is varied from 500 lmto3000lm to cre-
ate different electrode designs. For EW, an ac voltage with a
frequency of f ¼ 1 kHz and a maximum magnitude of 150 V
U
rms
is applied across the electrodes [Fig. 1(a)]. Thereafter, a
stream of vapour-air mixture at a flow rate of 3.6 l/min and a
temperature of 41:8
C is passed through a condensation
chamber, in which the substrate is maintained at a temperature
of 11:5
C. Throughout the condensation process, the substrate
is kept inside the condensation chamber and the vapour-air
mixture flow rate is kept constant . Condensation experiments
are performed without EW and under ac-EW by applying dif-
ferent magnitudes of U
rms
using straight and zigzag interdigi-
tated electrodes with l ¼ 500 lm, 1000 lm, and 3000 lm. The
condensation process, including the shedding events, is moni-
tored for 5 min using a high resolution camera.
In the absence of EW (U
rms
¼ 0 V), the condensate drops
are apparently randomly distributed with smaller average
sizes [Fig. 1(b-i); Movie S1 in the supplementary material]. In
contrast, under ac-EW with straight interdigitated electrodes,
the condensate drops with diameters comparable to the gap
width are aligned along the corresponding electrostatic energy
minimum locations at the gap centres [Fig. 1(b-ii); Movie
S2]. As discussed in our earlier study,
13
this alignment pro-
cess is accompanied by a sharp increase in the average drop
size. The latter is caused by the cascades of coalescence
events triggered by the EW-induced migration of the drops.
In this study, the underlying fact that the coalescence-induced
growth of the condensate drops under EW can be further
enhanced by moving the drops in a particular direction using
non-uniform electrical forces motivated the use of the zigzag
interdigitated electrodes towards altering the final shedding
characteristics. The converging gap geometry results in a net
downward electrical force on a condensate drop which moves
it towards the gap apex. Such sweeping of condensate drops
results in enhanced coalescence culminating in increased
growth of the average drop size. However, the droplets thus
mobilized eventually accumulate at the apices of the triangu-
lar gap elements due to the electrical trapping effect at these
locations [schematic in Fig. 1(a-iii)]. Hence, the condensate
droplet pattern under EW with zigzag interdigitated electrodes
also has a periodicity along the electrodes which is given by
l [compare Figs. 1(b-ii) and 1(b-iii),or1(b-iv)]. For longer l,
the condensate drops sweep a longer distance on the condens-
ing surface, resulting in on average larger sizes of the trapped
condensate droplets and also longer periodicity along the elec-
trodes [compare Figs. 1(b-iii) and 1(b-iv); Movies S3, S4, and
S5 show the condensate droplet pattern evolution correspond-
ing to l ¼ 1000 lm, 3000 lm, and 500 lm, respectively).
The final gravity-driven shedding characteristics are
quantified here by the average shedding radius hR
sh
i of the
FIG. 1. (a-i) Schematic of the substrate
used for the condensatio n experiments.
Schematics of the interdigitated elec-
trode (electrode-gap) designs are also
shown here—(a-ii) straight interdigi-
tated electrodes and (a-iii) zigzag inter-
digitated electrodes; the distance
l between the consecutive triangular ele-
ments is varied to create different elec-
trode designs. (b) Comparison between
condensate droplet patterns (at approxi-
mately the same time instant) (i) without
EW and under EW (U
rms
¼ 150 V;
f ¼ 1 k Hz) with different electrode
designs, (ii) straight interdigitated elec-
trodes, and zigzag interdigitated electro-
des with (iii) l ¼ 1000 lm and (iv)
l ¼ 3000 lm. Gravity points from top to
bottom along the electrodes. The yellow
bars in (b) represent 1 mm.
243703-2 Dey et al. Appl. Phys. Lett. 113, 243703 (2018)

condensate drops, and the average shedding rate hf
sh
i. hR
sh
i
represents the average value of R
sh
evaluated using an average
of more than 10 shedding events corresponding to a particular
EW condition, where R
sh
is evaluated using an image analysis
procedure [Fig. 2(a); see Sec. S1 in the supplementary mate-
rial]. The typical value of the percentage error involved is
16%. hf
sh
i is evaluated by dividing the total number of
recorded shedding events with the total time required for
those starting from the opening of the vapour valve for the ini-
tiation of the condensation process. Figure 2(b) clearly shows
that hR
sh
i progressively reduces under ac-EW, with straight
interdigitated electrodes, with increasing U
rms
; hR
sh
i for U
rms
¼ 150 V is approximately 50% smaller than that observed
without EW. Note that the values of R
sh
are typically larger
than the electrode pitch, and hence, the shedding drops cover
a few electrodes. In the absence of EW, hR
sh
i canbeesti-
mated from the balance between the droplet weight and the
inherent contact angle hysteresis (CAH) force acting on the
droplet
14
—hR
sh
i
ffiffi
3
p
q
k
c
ðD cos hÞ
1=2
.Here,k
c
¼
ffiffiffiffi
c
qg
q
is the
capillary length and c and q are the surface tension and the
density of water, respectively. D cos h is the difference
between the cosines of the receding and advancing contact
angles of water drops on the condensing surface; D cos h gives
a quantitative measure of the involved CAH (see Sec. S2 in
the supplementary material). It is now established that the
effective CAH under ac-EW in air gradually decreases with
increasing ac voltage.
15–17
This reduction in CAH is due to
the depinning of the droplet contact line from the random sur-
face heterogeneities induced by the oscillatory electrical
force, which is related to the associated oscillation of the
liquid-vapour interface.
15,18
The reduction in CAH with U
rms
can be expressed as D cos hðU
rms
ÞD cos h
0
abU
2
rms
,
where D cos h
0
is the value of D cos h for U
rms
¼ 0V,b is the
ratio of the effective dielectric capacitance per unit area and
c,anda is a coefficient characterizing the efficiency of the ac-
EW induced CAH reduction mechanism (generally a 1).
15,16
In this way, ac-EW reduces hR
sh
i with U
rms
for the case of
straight interdigitated electrodes [Fig. 2(b)]; hence, the corre-
sponding voltage dependent shedding radius can be estimated
as hR
sh
i
ffiffi
3
p
q
k
c
½D cos h
0
abU
2
rms
1=2
(also see Sec. S2 in
the supplementary material). It must be noted here that CAH
does not go on decreasing with increasing U
rms
but stabilize s at
a finite, albeit smaller, value at moderate values of U
rms.
15,16
Accordingly, the reduction in hR
sh
i is insignificant for higher
values of U
rms
[Fig. 2(b);Sec.S2inthesupplementary mate-
rial]. The gradually decreasing value of hR
sh
i, coupled with the
enhanced coalescence induced droplet growth under EW,
results in the increasing value of hf
sh
i [Fig. 2(c)]. In the case of
zigzag interdigitated electrodes [Fig. 2(d)], the non-uniform
overlap area between a condensate droplet footprint [the blue
filled circle in Fig. 2(d)] and the active electrode elements
results in a net electrical force on the droplet in the direction of
the converging gap. This net force is obtained by integrating
the vertical ð
^
vÞ component of the normal electrical force per
unit length ð
~
F
el
¼ F
el
^
n bcU
2
rms
^
nÞ along the droplet contact
line length on top of the electrode elements [Fig. 2(d);alsosee
Sec. S3 in the supplementary material]. This electrical force
sweeps the condensate drops towards the gap apices, thereby
enhancing coalescence and droplet growth. However, at the
gap apex, the orientation of the net vertical electrical force
FIG. 2. (ai) Representative image of a
condensate drop (outlined in red) about
to shed under gravity. The radius of
the drop at this instant is defined as the
shedding radius R
sh
. (aii) The conse-
quent frame showing the clearing of
the surface due to the droplet shedding.
(b) Variations of the average droplet
shedding radius hR
sh
i with the applied
voltage U
rms
for different electrode
designs, i.e., straight [Fig. 1(a-ii)] and
zigzag interdigitated electrodes with
different values of l [Fig. 1(a-iii)]; the
black solid curve with the black trian-
gles represents the theoretical esti-
mates corresponding to l ¼ 3000 lm
obtained using Eq. (1). (c) Variations
of the average shedding rate hf
sh
i with
U
rms
for the different electrode
designs. (d) Schematic of a condensate
droplet during dropwise condensation
under ac-EW with zigzag interdigi-
tated electrodes of varying l. The sche-
matic is not to scale.
243703-3 Dey et al. Appl. Phys. Lett. 113, 243703 (2018)

reverses the direction (from downward to upward) due to the
electrode geometry, which consequently traps the droplet at
that location [the dashed circle in Fig. 2(d) represents the foot-
print of the trapped droplet], in a manner similar to droplet
trapping by electrically tunable defects.
19
The condensate drops
thus accumulate at the gap apices till the droplet weight over-
comes the CAH force and the additional electrical trapping
force. So, for this case, hR
sh
i can be estimated from the relation
hR
sh
i
3
3
p
k
2
c
ðD cos h
0
abU
2
rms
ÞhR
sh
iþ
1:5
p
k
2
c
bU
2
rms
Dl
h
c
;
(1)
where the last term in Eq. (1) is due to the additional electri-
cal trapping force, Dl
h
c
represents the difference between the
horizontal projections of the total droplet contact line length
on the zigzag electrode elements above the horizontal droplet
footprint diameter and of the same below it, and a here takes
care of the possible non-uniformity in the ac-EW-induced
CAH reduction mechanism due to the zigzag electrode
geometry (also see Sec. S3 in the supplementary material).
Note that Dl
h
c
< 2hR
sh
i. Considering 2hR
sh
i as a scale for
Dl
h
c
, it can be inferred from Eq. (1) that for small values of
U
rms
, the reduction in CAH force and the additional electri-
cal trapping force [last two terms on RHS in Eq. (1)] almost
balance each other. Consequently, hR
sh
i for zigzag interdigi-
tated electrodes remains relatively unchanged for small val-
ues of U
rms
[Fig. 2(b)]. However, for large values of U
rms
,
the CAH force remains constant at a small finite value, while
the magnitude of the electrical trapping force progressively
increases ð/ U
2
rms
Þ. Hence, hR
sh
i increases with higher val-
ues of U
rms
for zigzag interdigitated electrodes [Fig. 2(b)].
Furthermore, Dl
h
c
in Eq. (1) increases with increasing l due to
the longer length of the droplet contact line on top of the elec-
trode elements with longer l [dashed electrode in Fig. 2(d)].
Accordingly, the electrical trapping force increases with
increasing l; consequently, hR
sh
i increases with increasing
l for a higher value of U
rms
[Fig. 2(b)]. Equation (1) provides
a reasonable estimate for hR
sh
i under ac-EW with zigzag
interdigitated electrodes, e.g., see the black solid curve with
the black triangles in Fig. 2(b) for rough theoretical estimates
of hR
sh
i for l ¼ 3000 lm (considering D cos h
0
0:13; b
8:5 10
6
F=ðNmÞ; a 0:8; Dl
h
c
Oð2hR
sh
iÞ). Finally,
the increasing value of hR
sh
i due to the electrical trapping
effect results in the lower shedding rate for the zigzag inter-
digitated electrodes, as compared to the straight interdigitated
electrodes [Fig. 2(c)].
Ac-EW with zigzag interdigitated electrodes indeed leads
to faster growth of condensate drops at earlier stages due
to the electrically induced droplet sweeping, as shown by
the temporal variations of the area-weighted average radius
of the condensate drops ðhriðtÞ¼Rr
3
=Rr
2
Þ [Fig. 3(a)]. hri
increases with increasing l [Fig. 3(a)] because the drops
sweep larger areas of the surface and thereby undergo more
coalescence before getting trapped, as can be seen in Fig.
1(b). However, this faster growth does not translate into a
higher shedding rate because of the electrostatic trapping
effect, as described before. The effect of electrostatic trapping
can be attenuated by applying U
rms
intermittently instead of
continuously, as shown in the inset in Fig. 3(b). During the
voltage-on phases, the sweeping and enhanced coalescence of
drops promote faster growth towards a radius k
c
[note that
in the absence of EW, hR
sh
iOðk
c
Þ]. Subsequently, the
voltage-off phases facilitate the gravity-driven shedding of
the sufficiently big condensate drops by turning off the
FIG. 3. (a) Temporal variations of the
area-weighted mean radius hri of the
condensate drops under ac-EW (U
rms
¼ 150 V) with different electrode
designs. (b) Variations of the average
shedding radius hR
sh
i with U
rms
under
continuous ac-EW (circles: straight
interdigitated electrodes; diamonds:
zigzag interdigitated electrodes with
l ¼ 3000 lm) and under intermittent
ac-EW (triangles: identical zigzag
interdigitated electrodes). The inter-
mittent ac-EW is achieved by switch-
ing the applied sinusoidal voltage on
(50 s) and off (10 s) as shown in the
inset. (c) Variations of the average
shedding rate hf
sh
i with U
rms
for con-
tinuous and intermittent ac-EW. (d)
Variations of the average volumetric
condensate removal rate h
_
v i with U
rms
for the different ac-EW conditions.
The symbols in (b)–(d) represent iden-
tical EW conditions.
243703-4 Dey et al. Appl. Phys. Lett. 113, 243703 (2018)

![FIG. 2. (ai) Representative image of a condensate drop (outlined in red) about to shed under gravity. The radius of the drop at this instant is defined as the shedding radius Rsh. (aii) The consequent frame showing the clearing of the surface due to the droplet shedding. (b) Variations of the average droplet shedding radius hRshi with the applied voltage Urms for different electrode designs, i.e., straight [Fig. 1(a-ii)] and zigzag interdigitated electrodes with different values of l [Fig. 1(a-iii)]; the black solid curve with the black triangles represents the theoretical estimates corresponding to l¼ 3000 lm obtained using Eq. (1). (c) Variations of the average shedding rate hfshi with Urms for the different electrode designs. (d) Schematic of a condensate droplet during dropwise condensation under ac-EW with zigzag interdigitated electrodes of varying l. The schematic is not to scale.](/figures/fig-2-ai-representative-image-of-a-condensate-drop-outlined-9aw9gxuz.png)