




read more









Research in several directions to extend the work presented in this paper are currently under way. Combining the indirect estimation methods with direct estimation could couple their respective strengths and would be a fruitful avenue of further research into signal grouping. Constructing a multidimensional feature space by combining the separate features could add value and this would obviously benefit future research outcomes.
Color images acquired were transformed to grey scale and pixel intensity values (consisting of 640 ∗ 480 = 307200 pixels per frame) of 100 frames were analyzed using raw pixel values.
Formulating the problem in the feature level rather than signal level will remove the requirement of preserving locality of thedata source.
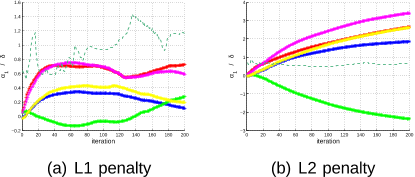
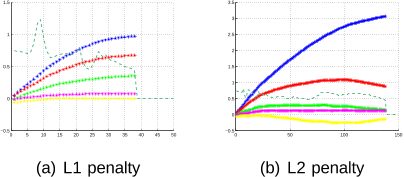
Applying the L1 norm penalty to the optimization produced faster convergence, occurring in iteration 72 compared to 110 iteration with L2 norm penalty.
In order to detect that the optimization has reached a local minima the variation of δ should be contained in a 1.5e−3 limit at least for a minimal convergence span of 5 iterations.
The maximisation of MI is achieved by maximising the entropies H(Y1) and H(Y2) and minimising the joint entropy, H(Y1, Y2) in (1).
due to the approximations in the objective function and the presence of local minima, the other mapping parameters have smaller non-zero vales.
The entropies H(Y1) and H(Y2) can be maximised by selecting the mapping parameters to make the data on the lower dimensional space resemble a uniform distribution.
the solution of the parameter vectors α1 and α2 should be sparse identifying the minimum number of nonzero elements naturally suggesting the use of the L1 norm as an appropriate penalty function.
Since the projections α1, α2 may be of very high dimensionality, it is assumed thatmin ‖α1‖1 = |α11 | + |α12 | + · · · |α1n | (16)Therefore the L1 penalty is∂ min ‖α1‖1 ∂Y1(17)further∂|α1| ∂Y11 = ∑n i=1 ∂|α1i | ∂Y11 = ∑ |X−11 |row1 sign|Y11 | ... ∂|α1| ∂Y1i = ∑n i=1 ∂|α1i | ∂Y1i = ∑ |X−11 |rowi sign|Y1i |resulting in∂ min ‖α1‖1 ∂Y1 = ∑ |X−11 | sign|Y1| (18)All iterative optimization methods require stopping criteria to indicate the successful completion of the process.
joint entropy H(Y1, Y2) can be minimised by selecting the mapping parameters to reflect the joint distribution, (Y1, Y2) is furthest away from a uniform distribution.
The laser beam of the range finder intersects horizontally at the abdominal area of the standing person capturing the movement of the book.
They proposed an unsupervised learning method by which the mappings g1(·) and g2(·) can be estimated indirectly, without computing mutual information.
The L1 norm performs equally well as the L2 norm on overdetermined system of equations while outperforming L2 norm for underdetermined problems [9] especially where the solution is expected to have fewer non zeros than 1/8 of the number of equations.