Direct finite element computation of non-linear modal coupling coefficients for reduced-order shell models

TL;DR: In this paper, the authors proposed a method for computing modal coupling coefficients for thin shells vibrating at large amplitude and discretized by a finite element (FE) procedure. But their method is not suitable for the case of a single oscillator.

Abstract: We propose a direct method for computing modal coupling coefficients--due to geometrically nonlinear effects--for thin shells vibrating at large amplitude and discretized by a finite element (FE) procedure. These coupling coefficients arise when considering a discrete expansion of the unknown displacement onto the eigenmodes of the linear operator. The evolution problem is thus projected onto the eigenmodes basis and expressed as an assembly of oscillators with quadratic and cubic nonlinearities. The nonlinear coupling coefficients are directly derived from the FE formulation, with specificities pertaining to the shell elements considered, namely, here elements of the "Mixed Interpolation of Tensorial Components" family. Therefore, the computation of coupling coefficients, combined with an adequate selection of the significant eigenmodes, allows the derivation of effective reduced-order models for computing--with a continuation procedure --the stable and unstable vibratory states of any vibrating shell, up to large amplitudes. The procedure is illustrated on a hyperbolic paraboloid panel. Bifurcation diagrams in free and forced vibrations are obtained. Comparisons with direct time simulations of the full FE model are given. Finally, the computed coefficients are used for a maximal reduction based on asymptotic nonlinear normal modes, and we find that the most important part of the dynamics can be predicted with a single oscillator equation.

Summary

1 Introduction

• Thin shells vibrating at large amplitude can exhibit complex dynamics.
• In conjunction with a numerical continuation method [3,4], or perturbation analytical methods [5], one is able to obtain complete bifurcation diagrams for free vibrations and forced responses of thin structures.
• Unfortunately, this strategy is restricted to simple geometries, for which ad-hoc functional bases made of simple – often analytical – functions can be constructed, ensuring convergence for a small number of modes.
• From the computation of the residual, and via algebraic manipulations, nonlinear coupling coefficients can be evaluated.
• The authors propose and implement a direct method with application to FE shells discretized with general shell elements of the MITC family (Mixed Interpolation of Tensorial Components) [18].

2 Direct computation of nonlinear stiffness

• This section gives the analytical and implementation details for the direct computation of the nonlinear coupling coefficients describing the geometrical nonlinearity of the shell.
• Other basis functions could have been used for the Galerkin projection, such as POD modes (Proper Orthogonal Decomposition, see for instance [20– 22]).
• As is well-known, shell finite elements suffer from very serious numerical pathologies when directly discretizing standard kinematical assumptions – namely, when using so-called “displacements-based elements”– see [18] and references therein.
• Therefore, the authors substitute for the above displacement-based strain vector the modified expression ˜ e = [err ess ers esr Irerz Irezr Isesz Isezs] t, Ir and Is denoting the interpolation operators, and likewise for the linear variations.
• Similar results up to machine precision have been obtained, hence validating the direct numerical computation of non-linear coefficients.

3 Application : a hyperbolic paraboloid panel

• The general methodology given in the previous section is now applied with a practical test case given by a shallow hyperbolic paraboloid panel.
• The first truncation T1 shown in the insert of Fig. 6 contains only the fundamental mode, and displays a hardening behavior.
• The transverse modes, with the lowest eigenfrequencies, are given for p=1 to 22 in Table 2.
• In the case of forced and damped vibrations, the amplitude responses predicted by the ROM and shown in Fig. 7 can be compared to direct simulations on the full FE model, so as to ascertain the quality of the ROM and its ability to predict the correct amplitude values.
• This might be ascribed to the fact that the 3:1 resonance is activated when the nonlinear frequencies share the perfect 3:1 relationship, and the complete model may feature a slight difference in the evolution of the higher frequencies versus vibration amplitude.

4 Conclusion

• A direct method has been presented for computing the nonlinear stiffness in geometric nonlinear vibration of thin shells discretized by finite elements.
• These formulas have been implemented in a FE code within the framework of MITC shell elements.
• The method gives fast and reliable computations for these coefficients, the accuracy of which has been validated by comparison with an indirect method.
• The computation of these coefficients can be used for deriving reducedorder models of great accuracy, allowing for precise prediction of nonlinear vibration characteristics of shell models.
• Such studies will also allow a more extensive assessment of the criterion used in the present paper to select the important modes in the ROM, which can lead to an automatized selection procedure.

Figures

Fig. 2 Hyperbolic paraboloid panel used for the simulations, mesh composed of 4624 quadrangles (Nn=4761 nodes).

Table 1 M-mode family: label p of their appearance in increasing frequency order, radian eigenfrequency ωp and its ratio to the fundamental ω1, and quadratic coupling coefficients with mode p=1, gp 11 .

Table 2 B-modes, radian eigenfrequency ωp and ratio to the fundamental ω1.

Fig. 9 Forced response of the HP panel, forcing amplitude F=150 N, comparison between ROM and full FE model. (a): frequency-response function. Solid and dotted blue lines: stable and unstable solutions, maximum of first coordinate X1 of the ROM. Red lines: maximum of sixth coordinate X6. Circles (◦): maximum amplitude value of the displacement at center w(0, 0, t) inferred from a direct time simulation of the full FE model. (b): phase portrait ẇ(0, 0, t) versus w(0, 0, t) for the full FE model (black dotted line) and the ROM (blue solid line), for Ω=0.85ω1, (c): Ω=0.97ω1, (d): Ω=1.6ω1.

Fig. 7 Frequency-response function of the HP panel, modal damping ratio ξ=0.05 for each mode, harmonic pointwise forcing of varying frequency Ω and force F applied at center of the panel. F=50 N and F=150 N.

Fig. 10 Frequency-response functions for the forced response of the HP panel, (a): forcing amplitude F=50 N and (b): 150 N. Comparison between ROMS: blue (ref): 20 linear modes, red (LNM): a single linear mode and black (NNM): a single nonlinear normal mode.

Fig. 4 Convergence of four eigenfrequencies of the HP panel for increasing number of nodes Nn in the mesh. (a) p=1, fundamental eigenfrequency, (b) p=20, (c) p=40, (d) p=224, corresponding to the

Fig. 5 Convergence of the nonlinear cubic coefficient hpp,p,p, with respect to the number of nodes Nn of the mesh. (a): p=1, (b) p=20, (c) p=40.

Fig. 3 Five eigenmodes shapes of the HP panel. Each row displays a given mode, with two in-plane displacements u and v and transverse displacement w in successive columns.

Fig. 1 MITC4 shell element tying points (esz tying points obtained by symmetry)

Fig. 8 Forced response of the HP panel, forcing amplitude F=50 N, comparison between ROM and full FE model. (a): frequency-response function. Solid and dotted lines: stable and unstable solutions, maximum of first coordinate X1 of the ROM. Circles (◦): maximum amplitude value of the displacement at center w(0, 0, t) inferred from a direct time simulation of the full FE model. (b): phase portrait ẇ(0, 0, t) versus w(0, 0, t) for the full FE model (black dotted line) and the ROM (blue solid line), for Ω=0.6ω1. (c): idem for Ω=1.4ω1.

Fig. 6 Backbone curve of the fundamental mode of the HP panel, convergence study. Insert: convergence of the backbone for an increasing number of M-modes and a single B-mode. T1: fundamental T-mode only – T2: fundamental T-mode + 3 M-modes (224, 280 and 347) – T3: fundamental + 7 M-modes (modes 371, 388, 427 and 493 added) – T4: fundamental + 9 M-modes (502, 522 added). Main figure: Convergence of the backbone curve for an increasing number of B-modes, for a fixed number (7) of M-modes. T5: B-modes 2 to 6 added – T6: B-modes 1 to 13 plus 17 and 22 – T7: B-modes 1 to 22. X1: main coordinate, X6 and X17: two most important non-resonant couplings, X22: internally resonant coordinate. Unstable states represented with dash-dotted lines.

Full text

HAL Id: hal-00955582
https://hal.inria.fr/hal-00955582
Submitted on 4 Mar 2014
HAL is a multi-disciplinary open access
archive for the deposit and dissemination of sci-
entic research documents, whether they are pub-
lished or not. The documents may come from
teaching and research institutions in France or
abroad, or from public or private research centers.
L’archive ouverte pluridisciplinaire HAL, est
destinée au dépôt et à la diusion de documents
scientiques de niveau recherche, publiés ou non,
émanant des établissements d’enseignement et de
recherche français ou étrangers, des laboratoires
publics ou privés.
Direct nite element computation of non-linear modal
coupling coecients for reduced-order shell models
Cyril Touzé, Marina Vidrascu, Dominique Chapelle
To cite this version:
Cyril Touzé, Marina Vidrascu, Dominique Chapelle. Direct nite element computation of non-linear
modal coupling coecients for reduced-order shell models. Computational Mechanics, Springer Verlag,
2014, 54, pp.567-580. �10.1007/s00466-014-1006-4�. �hal-00955582�

Noname manuscript No.
(will be inserted by the edit or )
Direct finite element computation
of non-linear modal coupling coefficients
for reduced-order shell models
C. Touz´e · M. Vidrascu · D . Chapelle
Computational Mechanics, DOI:10.1007/s00466-014-1006-4
Abstract We propose a direct metho d for computing modal coupling coef-
ficients – due to geometrically nonlinear effects – for thin shells vibrating at
large amplitude and discretized by a finite element (FE) p r ocedure. These
coupling coefficients arise when consi de ri n g a discrete e xpan s ion of the un-
known displacement onto the ei gen modes of the linear operator. The evolu-
tion problem is thus projected onto the eigenmodes basis and expressed as an
assembly of oscillators with quadratic and cubic nonlinearities. The nonlinear
coupling coefficients are directly derived from the finite element formulation,
with specificities per t ain i ng to the shel l elements considered, namely, here ele-
ments of the “Mixed Interpolati on of Tensorial Components” family (MI TC) .
Therefore, the computati on of coupling coefficients, combined with an ade-
quate selection of the significant eigenmodes, allows the derivation of effective
reduced-order models for compu t in g – with a continuation procedure – the sta-
ble and unstable vibratory states of any vibrating shell, up to large amplitudes.
The procedure is illustr at ed on a hyperbolic paraboloid panel. Bifurcation di-
agrams in free and forced vibrat ion s are obtained. Comparisons with direct
time simulations of the full FE model are given. Finally, t he computed coeffi-
C. Touz´e
Unit´e de M´ecanique (UME),
ENSTA-ParisTech, 828 Boulevard des mar´echaux,
91762 Palaiseau Cedex, France
Tel.: +33-1-69-31-97-34
E-mail: cyril.touze@ensta-paristech.fr
M. Vidrascu
Inria/Reo and LJLL UMR 7958 UPMC,
Rocque nc ourt, B.P. 105, 78153 Le Chesnay, France
E-mail: marina.vidrascu@inria.fr
D. Chapelle
Inria/MΞDISIM, 1 rue Honor´e d’Estienne d’Orves,
Campus de l’Ecole Polytechnique, 91120 Palaiseau, France
E-mail: dominique.chapelle@inria.fr

2 C. Touz´e et al.
cients are used for a maximal reduction based on asymptotic nonlinear normal
modes ( NNM s) , an d we find that the most important part of the dynamics
can be predicted with a single oscillator equation.
Keywords geometric n onl i ne ar ity · finite elements · MITC elements ·
stiffness evaluation · bifurcation diagram · reduced-ord er models
1 Intro d u ct ion
Thin shells vibrating at large amplitude can exhibit complex dynamics. These
geometrically nonlinear behaviors occur as soon as the vibration amplitude is
of the order of the thickness, and may induce various nonlinear effects such
as jumps, instabilities, quasi-periodic or chaotic vibrat ion s [1, 2]. In turn, this
may lead to undesirable vib rat i on patterns that can have detrimental effects
on the usual predicted behavior of numerous engineering systems, such as
sudden increase in vibration amplitudes, fatigue of components, etc.. In or-
der to have a significant understanding of the possible nonlinear behaviors
of a given structure, the computation of a complete bifurcation diagram is
key, as it gives access to all th e solution branches (stable and unstable) un-
der variations of some selected control parameters. For that purpose, direct
numerical integration generally appears as cumbersome and inappropriate, as
unstable states are not accessible to the computation. Moreover, computing
all t h e solution branches by successive runs, given variabl e initial conditions,
is so ti m e-c ons um in g that the method is usually not considered.
In this context, reduced-order models (ROMs) are gen er al l y much better
adapted. In conjunction with a numerical continuation method [3,4], or per-
turbation analytical methods [5], one is ab le to obtain complete bifurcation
diagrams for free vibrations and forced respon se s of thin structures. In the last
years, many applications have been pursued usi ng this methodology, i n order
to compute frequency response curves of thin structur es harmonically forced in
the vicinity of one of its eigenmodes, see e.g. [5,2,6–9]. In most contributions,
the Partial Differential Equations (PDEs) of motion for a given shell model
– following e.g. von K´arm´an assumptions, or Donnel l shallow-shell theory, see
e.g. [10] – is discretized by using the eigenmodes of the linear operator, or a
given ad-hoc func t i onal basis that satisfi es the boundary conditions. Applying
a Galerkin pro c ed ur e, the problem is then transformed into a dynamical sys-
tem by conserving the important modes, for which continuation methods can
thus be applied. Unfortunately, this strategy is restricted to simple geometries,
for which ad-hoc functional bases made of simple – often analytical – func-
tions can be constructed, ensuring convergence for a smal l number of modes.
For a general shell geometry, finding such a specific discretization method is
much more di ffic ul t , see e.g. [11] for a proposed approach based on so-called
R-functions.
For complex geometries the most common framework consists in using
the versatility of finite-elements (FE) procedures. However, at the time being,

Title Suppressed Due to Excessive Length 3
there exists no contribution on reduce d- orde r models based on shell finite el-
ements for predicting bifurcation diagrams by a continuation method. More
precisely, first attempts toward this general objecti ve can be found in [12] for
beam-like structures, and in [13,14] for rectangular plat es. The present paper
aims at proposing a complete strategy specifically adapted to tackle the most
general case of thin shells. The main difficulty resides in the computation of the
ROM from th e FE discretized shell. A simple strategy that is used in th is con-
tribution consist s in uti l iz i ng the e ige nm odes basis in the construction process
of the ROM. The dynamical problem, expressed onto the linear eigenmodes, is
represented by an assembly of oscillators with qu ad rat i c and cubic nonlinear-
ities, arising from the geometricall y nonlinear terms. Within that framework,
numerous nonlinear coupling coefficients appear in the dynamical system, and
one needs to evaluate these coefficient s in order to build the ROM.
Indirect d et er mi n at i on of these nonlinear coupling coefficients has already
been proposed. Muravyov [15], then Mignolet and Soize [16] used a so-called
STEP method (STiffness Evaluation Procedure) for that purpose. The ide a
is to prescribe in the structural model numerous selected static deformations,
taken from one of the eigenmodes or a combination thereof. From the c om-
putation of the residual, and via algebraic manipulations, nonlinear coupling
coefficients can be evalu at ed . A review of the computational schemes, as well
as their applications to solve numerous engineering problems involving for ex-
ample random vibrati on s, is given in [17]. The main advantage of the STEP
method is that one can use any commercial finite element software, as there
is no need to compute specific finite element quantities, and only standard
computations with specific post-processing allow to derive the desired coeffi-
cients. The drawback of this indirect method is that numerous well-selected
combinations of static deformations must be considered; moreover, the method
requires prescribing an appropriate amplitude for the static deflections.
In this contribution, we propose and implement a direct method with ap-
plication to FE shel ls discretized with general shell elements of the MITC
family (Mixed Interpolation of Tensorial Components) [ 18] . First an analyti-
cal expression of t h e nonlinear coupling coefficients is derived from the internal
potent i al energy. The FE procedure an d implementation details are then given.
Next, the method is applied to a clamped hyperbolic paraboloid panel. In this
case, the detailed derivation of ROMs is explained, and bifurcation diagrams
in free and f orc ed vibr at i ons are given.
2 D ir ect computation of nonlinear stiffness
This section gives the analy t i cal and implementation details for the direct
computation of the nonlinear coupling coefficients describing the geometrical
nonlinearity of the shell. The l i n ear modes basis is used to discretize the FE
problem, and specificities related to the use of the chosen shell elements are
then thoroughly explained so as to highlight the practical i m pl em entation of
the calculation in a given shell FE code.

4 C. Touz´e et al.
2.1 Formulation
This section is devoted to the analytical expressions of the nonlinear coupling
coefficients. Geometric nonlinearity is assumed, which means th at the mate-
rial has a linear elastic behavior, but t he shell can undergo large amplitude
motions. In this context, the nonlinearit i es can be directly derived from the
variations of internal elastic energy δW
int
, w hi ch read
δW
int
=
Z
Ω
Σ
: δe, (1)
where Σ is the second Piola-Kirchhoff stress te ns or and e the Green-Lagrange
strain tensor. The strain-displacement relationship is
e =
1
2

∇
+ ∇
t
+ ∇
t
.∇

y
, (2)
where y stands for the displac eme nt. For simplicity, l e t us denote by ε the
linear part of the s t rai n -d i sp lac eme nt rel ati on sh i p
ε =
1
2

∇
+ ∇
t

y
, (3)
and e
(2)
the quadratic part
e
(2)
=
1
2

∇
t
y
.∇ y

. (4)
A li n ear elas t i c and isotropic mater i al is assumed, so that we have
Σ
= H : e, (5)
where H stands for the constitutive tensor associated with a Saint-Venant-
Kirchhoff material, namely, Hooke’s law.
Then we have
δW
int
=
Z
Ω

ε
+ e
(2)

: H
:

δε + δe
(2)

. (6)
From this last equation, one can identify the linear, quadrat i c and cubic terms
(as functions of the displacement), which are denoted respectively by δW
1
,
δW
2
et δW
3
δW
1
=
Z
Ω
ε
: H : δε, (7)
δW
2
=
Z
Ω
e
(2)
: H
: δε + ε : H : δe
(2)
, (8)
δW
3
=
Z
Ω
e
(2)
: H
: δe
(2)
. (9)

Frequently asked questions

Q1. What have the authors contributed in "Direct finite element computation of non-linear modal coupling coefficients for reduced-order shell models" ?

The authors propose a direct method for computing modal coupling coefficients – due to geometrically nonlinear effects – for thin shells vibrating at large amplitude and discretized by a finite element ( FE ) procedure. The evolution problem is thus projected onto the eigenmodes basis and expressed as an assembly of oscillators with quadratic and cubic nonlinearities. 

Q2. What future works have the authors mentioned in the paper "Direct finite element computation of non-linear modal coupling coefficients for reduced-order shell models" ?

It also paves the way for further fine numerical studies of bifurcation diagrams for shells of arbitrary complex geometry. Such studies will also allow a more extensive assessment of the criterion used in the present paper to select the important modes in the ROM, which can lead to an automatized selection procedure. 

Q3. What is the key to a complete bifurcation diagram?

In order to have a significant understanding of the possible nonlinear behaviors of a given structure, the computation of a complete bifurcation diagram is key, as it gives access to all the solution branches (stable and unstable) under variations of some selected control parameters. 

Q4. What is the method for obtaining complete bifurcation diagrams?

In conjunction with a numerical continuation method [3,4], or perturbation analytical methods [5], one is able to obtain complete bifurcation diagrams for free vibrations and forced responses of thin structures. 

Q5. What is the method used for calculating the nonlinear coupling coefficients?

Analytical expressions of the nonlinear coupling coefficients have been expressed from the internal elastic energy by using a modal expansion for the displacement. 

Q6. What is the first physical effect that the reduced-order model must capture?

The first physical effect that the reduced-order model must mandatorily capture is the coupling between bending and membrane motions. 

Q7. How is the ROM used to predict the response of a thin shell?

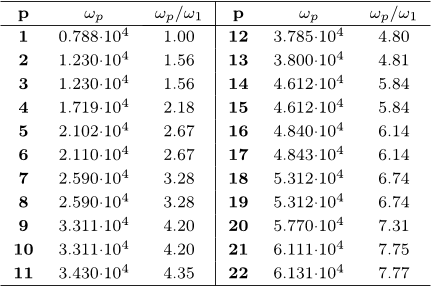
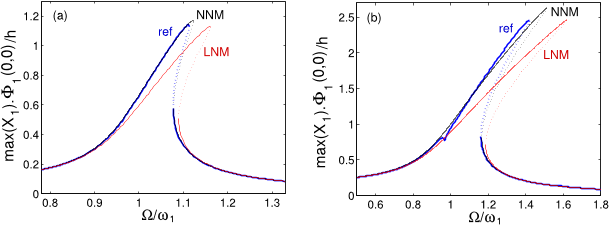
A converged ROM including 20 linear modes has been shown to predict with excellent accuracy the resonant response of a HP panel in the vicinity of its fundamental frequency. 

Q8. What is the way to compute the convergence of the reduced-order model?

As peculiar nonlinear phenomena will be exhibited, a very good accuracy on all the numerical values is needed so as to ensure a good convergence of the reduced-order model. 

Q9. What is the effect of the internal resonance tongue on the global dynamics of the forceddamped system?

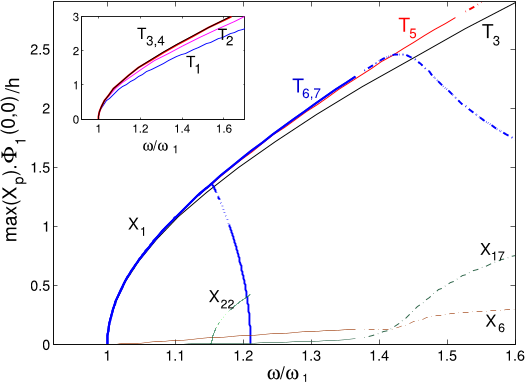
An internal resonance tongue has been found with mode 22, albeit it occurs in a very narrow interval, so that its effect on the global dynamics of the forceddamped system is likely to be negligible. 

Q10. Why do the authors use linear eigenmodes as a projection basis?

the authors specifically select linear eigenmodes as a projection basis for the following two reasons:– it allows for a decoupling between linear components, – eigenmodes are easily computable in any standard FE code. 

Q11. What is the way to compute the bifurcation diagram?

The reduced-order model may be used for either direct time integration, or, as shown next, for computing by a continuation method the bifurcation diagram in the vicinity of a given dynamical state. 

Q12. What is the effect of the absence of stable periodic orbit?

This absence of stable periodic orbit is consistent with previous studies on the transition to turbulence for thin plates and shells, see e.g. [34–36], where it has been found that from vibration amplitudes of 2 to 4h (depending on the structure considered), no stable periodic solutions exist anymore, so that the dynamical solution is at least quasi-periodic. 

Q13. What is the effect of the internal resonance tongue on the frequency response in the forced-damped?

it has been emphasized in [36] that when the internal resonance occurs in a narrow interval as here observed, its influence on the frequency response in the forced-damped system is negligible. 

Q14. What is the first one in increasing frequency order that shows a strong coupling with the fundamental?

Concerning the M-modes, the mode labeled 224 is the first one in increasing frequency order that shows a strong coupling with the fundamental mode and thus will be key in the selection procedure explained in the next section. 

Q15. What is the effect of adding the modes in order to reproduce the nonlinear vibrating behavior?

One observes that the hardening behavior is less pronounced, which reveals the effect of adding those modes in order to correctly reproduce the nonlinear vibrating behavior of the panel. 

Q16. How long does the amplitude limit of the HP panel converge?

The amplitude limit in the case presented here of the HP panel is found to converge to a value of 2.3h, as shown by the last two truncations which are superimposed, T6 and T7. 

Q17. Why do the authors need to deal with nonlinear tensors?

This is because the authors need to deal with non-symmetric tensors for the computations of the nonlinear stiffness coefficients in (14)-(15), since the tensor ∇tΦi. 

Q18. What is the amplitude of the transverse displacement at the center of the ROM?

For the full FE model, the maximum amplitude of the transverse displacement at the center is shown, whereas for the ROM the continuation software AUTO gives the maximum amplitude of each coordinate Xp, without their relative phases, so that one is not able to reconstruct precisely the complete transverse displacement by adding all modal coordinates according to Eq. (10). 

Q19. How do the authors compute the coefficients gpij and h p ijk?

In order to compute the coefficients gpij and h p ijk consistently with the finite element procedure, the authors thus need to modify the components of the second-order tensors ∇tΦi. 

Q20. What is the convergence with the number of high-frequency modes?

The convergence with this number of high-frequency modes is shown in the insert of Fig. 6, where only the fundamental B-mode is retained with an increasing number of M-modes.