Q2. How many channels were collected in the study?
Seventy-four channel ERPs were collected in 10 English-speaking exchange students to Switzerland while reading single-German words.
Q3. What is the amplitude of the estimated covariance map b?
The amplitudes of the estimated covariance map b depend on the variance of V, on the variance of X, and on the strength of the relation between V and X.
Q4. What is the common method of establishing the statistical significance of difference maps?
In order to establish the statistical significance of such difference maps, one can either use the standard multivariate statistical approaches such as MANOVA (Vasey and Thayer, 1987).
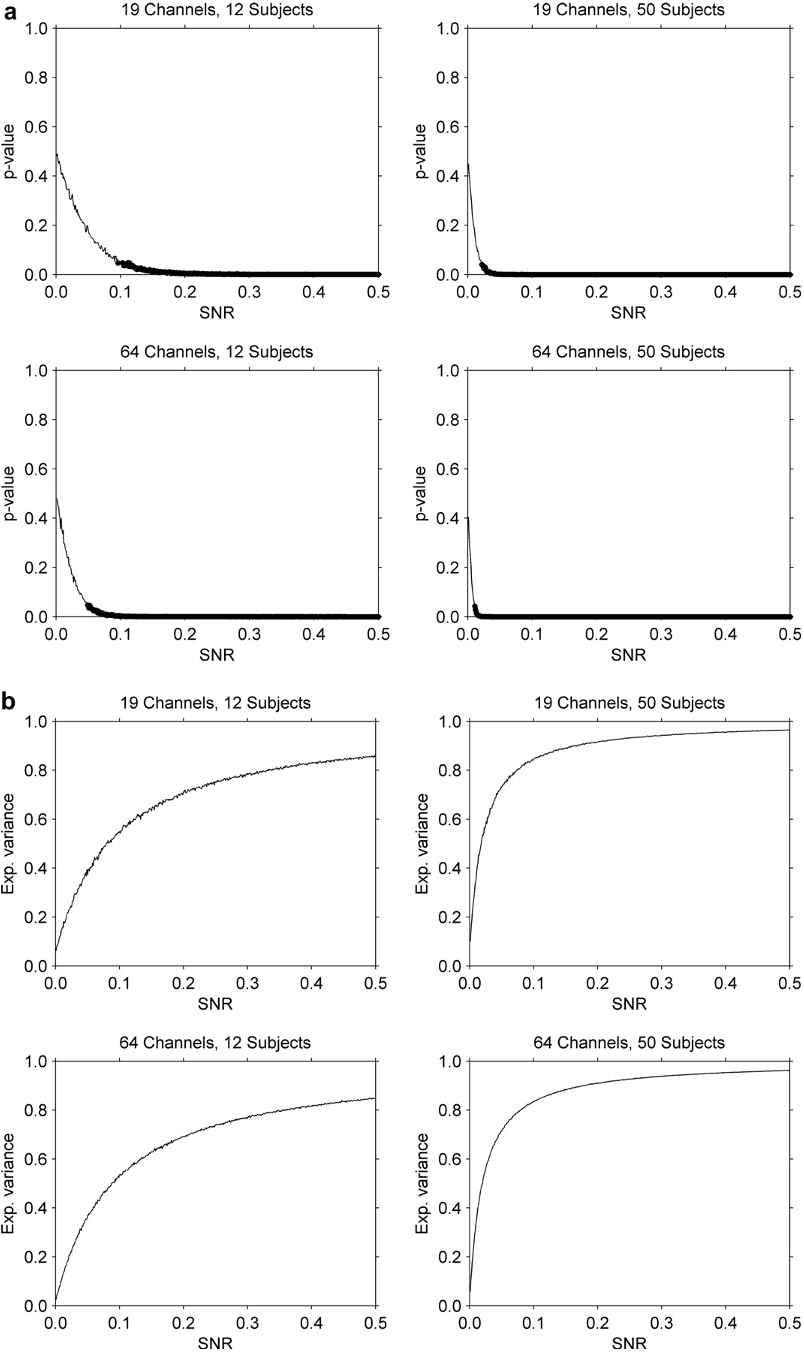
Q5. What is the effect of increasing the number of subjects or electrodes?
Increasing the number of subjects or electrodes improves the sensitivity of the method, and effects can be detected at lower SNRs.