DRAFT
EVENT-TRIGGERED REAL-TIME SCHEDULING
OF STABILIZING CONTROL TASKS
PAULO TABUADA
Abstract. In this note we revisit the problem of scheduling stabilizing control tasks on embed ded processors.
We start from the paradigm that a real-time scheduler should be regarded as a feedback controller that decides
which task is executed at any given instant. This controller has for objective guaranteeing that software tasks
meet its deadlines and that stabilizing control tasks asymptotically stabilize the plant. According to this
feedback paradigm, the decision of executing control tasks should not be based on release times and deadlines
but rather on the state of the plant. We investigate the fea sibili ty of a simple event-triggered scheduler based
on the state norm and provide some schedulability results.
1. Introduction
Small embedded microprocessors are quickly becoming an essential part of the most diverse applications. A
particularly interesting example are physically distributed sensor/actuator networks responsible for collecting
and processing information, and to react to this information through actuation. The embedded microprocessors
forming the computational core of these networks are required to execute a variety of tasks comprising the relay
of information packets in multi-hop communication schemes, monitoring physical quantities, and computation
of feedback control laws. Since we are dealing with resource limited microprocessors it becomes important
to asse ss to what extent we can increase the functionality of these embedded devices through novel real-time
scheduling algorithms based on event-triggered rather than time-triggered execution of control tasks.
We investigate in this note a very simple event-triggered scheduling algorithm that preempts running tasks to
execute the control task whenever a certain error becomes large when compared with the state norm. This
idea is an adaptation to the scheduling context of several techniques used to study problems of control under
communication constraints [NE00, BL00, EM01]. We take explicitly into account the execution time of the
control task and show that the proposed scheduling policy guarantees global asymptotical stability. We also
provide sufficient conditions for co-schedulability of the control task with other tasks competing for processor
time. The proposed approach is illustrated with simulation results.
Real-time scheduling of control tasks has received renewed interest from the academic community in the past
years [SLCB00, CE00, ACR
+
00, CEBA02, BA02, CLS03, LHLQ06]. Common to all these approaches is
the underlying principle that better control performance is achieved by providing more CPU time to control
tasks. This can be accomplished in two different ways: letting control tasks run for longer amounts of
time using anytime implementations or model predictive controllers; or by scheduling control tasks more
frequently. All these approaches assume the existence of a performance criterion for the control task such as
a cost function used to design an optimal linear quadratic regulator. Scheduling strategies are then obtained
through optimization algorithms seeking to determine schedules maximizing the performance criterion. The
work presented in this note does not resort to optimization and does not require a performance criterion.
Instead, the decision to execute the control task is determined by a feedback mechanism based on the state of
the plant.
Closer to the results presented in this note is the work described in [PPV
+
02, PPBSV05], where resource
allocation and feedback control are designed in an integrated fashion. Several concurrent controllers described
This research was partially supported by the National Science Foundation EHS award 0509313.
1

DRAFT
2 PAULO TABUADA
by scalar gains and activation rates of the corresponding processes are designed so as to ensure stability of the
controlled processes as well as real-time schedulability. Close at the technical level, although addressing very
different problems, is the recent work on stabilization under communication constraints [NE00, BL00, EM01,
BPZ02, Lib03, NT04]. All these approaches are concerned with the stabilization of continuous systems under
reduced communication and the employed techniques share with some of the techniques described in this note
a common ancestor: the perturbation approach to stability analysis of control systems, described for example
in [Kha96]. Similar techniques have also been used in [LNT02] to show how sample-and-hold implementations
of stabilizing controllers guarantee stability under sufficiently fast time-triggered executions. Finally, we would
like to refer the reader to [AB02] where some advantages of event-driven control over time-driven control are
presented in a stochastic setting. A preliminary version of the results presented in this note was reported
in [TW06].
2. Notation and problem statement
2.1. Notation. We shall use the notation |x| to denote the Euclidean norm of an element x ∈ R
n
. Given
matrices A and B, [A|B] denotes the matrix formed by the columns of matrix A followed by the columns of
matrix B. A function f : R
n
→ R
m
is said to be Lipschitz continuous on compacts if for every compact set
S ⊂ R
n
there exists a constant L > 0 such that:
|f(x) − f(y)| ≤ L|x − y|
for every x, y ∈ S. A continuous function α : [0, a[→ R
+
0
, a > 0, is said to be of class K if it is strictly
increasing and α(0) = 0. It is said to be of class K
∞
if a = ∞ and α(r) → ∞ as r → ∞.
2.2. Problem statement. We consider a control system:
(2.1) ˙x = f(x, u), x ∈ R
n
, u ∈ R
m
for which a feedback controller:
(2.2) u = k(x)
has been designed rendering the closed loop system:
(2.3) ˙x = f(x, k(x + e))
Input-to-State Stable (ISS) with respect to measurement errors e ∈ R
n
. We shall not need the definition
1
of
ISS in this note but rather the following characterization.
Definition 2.1. A smooth function V : R
n
→ R
+
0
is said to be an ISS Lyapunov function for the closed loop
system (2.3) if there exist class K functions α, α, α and γ satisfying:
α(|x|) ≤ V (x) ≤ α(|x|)(2.4)
∂V
∂x
f(x, k(x + e)) ≤ −α(|x|) + γ(|e|)(2.5)
Closed loop system (2.3) is said to be ISS with respect to measurement errors e ∈ R
n
if there exists an ISS
Lyapunov function for (2.3).
The implementation of the feedback law (2.2) on an embedded processor is typically done by sampling the
state at time instants:
t
0
, t
1
, t
2
, t
3
, t
4
. . .
computing u(t
i
) = k(x(t
i
)) and updating the actuator values at time instants:
t
0
+ ∆, t
1
+ ∆, t
2
+ ∆, t
3
+ ∆, t
4
+ ∆, . . .
1
See, for example, [Son04] for an introduction to ISS and related notions.

DRAFT
EVENT-TRIGGERED REAL-TIME SCHEDULING OF STA BILIZING CONTROL TASKS 3
where ∆ ≥ 0 represents the time required to read the state from the sensors, compute the control law and
update the actuators. This means that to a sequence of measurements:
x(t
0
), x(t
1
), x(t
2
), x(t
3
), x(t
4
), . . .
there corresponds a sequence of actuation updates:
u(t
0
+ ∆), u(t
1
+ ∆), u(t
2
+ ∆), u(t
3
+ ∆), u(t
4
+ ∆), . . .
Between actuator updates the input value u is held constant according to:
(2.6) t ∈ [t
i
+ ∆, t
i+1
+ ∆[ =⇒ u(t) = u(t
i
+ ∆)
Furthermore, the sequence of times t
0
, t
1
, t
2
, t
3
, t
4
, . . . is typically periodic meaning that t
i+1
− t
i
= T where
T > 0 is the period. We can thus regard the execution of the control task implementing the control law (2.2)
as being time-triggered. In this note we consider instead event-triggered executions where the sequence
t
0
, t
1
, t
2
, t
3
, t
4
. . . of execution times is no longer periodic neither specified in advance but rather implicitly
defined by an execution rule based on the state of the plant. To introduce this execution rule we define the
measurement error e to be:
(2.7) t ∈ [t
i
+ ∆, t
i+1
+ ∆[ =⇒ e(t) = x(t
i
) − x(t)
We can thus describe the evolution of (2.1) under the implementation (2.6) of control law (2.2) by:
˙x = f(x, k(x + e))
with e ∈ R
n
as defined in (2.7).
Let us first consider the hypothetical case ∆ = 0 with the single purpose of explaining the execution rule.
From (2.5) we see that if we restrict the error to satisfy:
(2.8) γ(|e|) ≤ σα(|x|), σ > 0
the dynamics of V is bounded by:
∂V
∂x
f(x, k(x + e)) ≤ (σ − 1)α(|x|)
thus guaranteeing that V decreases provided that σ < 1. Inequality (2.8) can be enforced by executing the
control task when:
(2.9) γ(|e|) ≥ σα(|x|)
since ∆ = 0 implies that if the control task is executed at time t
i
we will have e(t
i
) = x(t
i
) − x(t
i
) = 0 and
γ(|e(t
i
)|) = 0 thus enforcing (2.8). When ∆ > 0, the control task needs to be executed before the inequality
γ(|e|) ≥ σα(|x|) is satisfied in order to account for the delay ∆ between measuring the state and updating the
actuators.
Although the simple execution rule (2.9) guarantees global asymptotical stability by construction, there are
three important questions that need to be answered in order to assess the feasibility of this scheduling policy:
(1) Since the execution times are only implicitly defined, can we guarantee that they will not become
arbitrarily close resulting in an accumulation
2
point?
(2) In the absence of accumulation points, can we compute an estimate of the time elapsed between
consecutive executions of the control task?
(3) How can we use the execution rule (2.9) when there are more tasks competing for processor time and
still guarantee that no deadlines are missed?
Answering the above questions is the objective of the following sections.
2
In the context of hybrid systems this corresponds to another example of the infamous Zeno behavior [ATS06 ].

DRAFT
4 PAULO TABUADA
3. Existence of a lower bound for inter-execution times
We start immediately with one of the main contributions of this note.
Theorem 3.1. Let ˙x = f(x, u) be a control system and let u = k(x) be a control law rendering the closed loop
system ISS with respect to measurement errors. If the following assumptions are satisfied:
(1) f : R
n
× R
m
→ R
n
is Lipschitz continuous on compacts;
(2) k : R
n
→ R
m
is Lipschitz continuous on compacts;
(3) There exists an ISS Lyapunov function V for the closed loop system satisfying (2.5) w ith α
−1
and γ
Lipschitz continuous on compacts,
then, for any compact set S ⊂ R
n
containing the origin, there exists an ε > 0 such that for all ∆ ∈ [0, ε] there
exists a time τ ∈ R
+
such that for any initial condition in S the inter-execution times {t
i+1
− t
i
}
i∈N
implicitly
defined by the execution rule (2.9) are lower bounded by τ, that is, t
i+1
− t
i
≥ τ for any i ∈ N.
Proof. Let R be the compact se t defined by all the points x ∈ R
n
satisfying V (x) ≤ µ where µ > 0 is large
enough so that S ⊂ R. Such µ always exists since by (2.4) V is proper or radially unbounded. Set R is forward
invariant for the closed loop system since the execution rule (2.9) guarantees
˙
V ≤ 0. We now define another
compact set E by all the points e ∈ R
n
satisfying |e| ≤ γ
−1
(σα(|x|)) for all x ∈ R. Since α
−1
and γ are
Lipschitz continuous on compacts, then so is α
−1
(γ(|r|)/σ). Let P be the Lipschitz constant for the compact
set E so that |α
−1
(γ(|r|)/σ) − α
−1
(γ(|s|)/σ)| ≤ P |r − s|. If r = e and s = 0 we obtain α
−1
(γ(|e|)/σ) ≤ P |e|.
Note that by enforcing P |e| ≤ |x| we guarantee α
−1
(γ(|e|)/σ) ≤ |x| (which is (2.8)) so that if suffices to
show that the inter-execution times are bounded for the execution rule P |e| ≥ |x|. As a first step towards
showing boundedness we note that it follows from Lipschitz continuity on compacts of f(x, u) and k(x) that
f(x, k(x + e)) is also Lipschitz continuous on compacts, that is:
|f(r, k(r + s)) − f(r
0
, k(r
0
+ s
0
))| ≤ L|(r, s) − (r
0
, s
0
)|
by taking r = x, s = e and r
0
= 0 = e
0
we obtain:
(3.1) |f(x, k(x + e))| ≤ L|(x, e)| ≤ L|x| + L|e|
when (x, e) ∈ R × E. Note that R × E is forward invariant for the state as well as the error dynamics. We
can now bound the inter-event times by looking at the dynamics of |e|/|x|.
d
dt
|e|
|x|
=
d
dt
(e
T
e)
1/2
(x
T
x)
1/2
=
(e
T
e)
−1/2
e
T
˙e(x
T
x)
1/2
− (x
T
x)
−1/2
x
T
˙x(e
T
e)
1/2
x
T
x
= −
e
T
˙x
|e||x|
−
x
T
˙x
|x||x|
|e|
|x|
≤
|e|| ˙x|
|e||x|
+
|x|| ˙x|
|x||x|
|e|
|x|
=
1 +
|e|
|x|
| ˙x|
|x|
≤
1 +
|e|
|x|
L|x| + L|e|
|x|
by (3.1)
= L
1 +
|e|
|x|
1 +
|e|
|x|
(3.2)
If we denote |e|/|x| by y we have the estimate ˙y ≤ L(1 + y)
2
and we conclude that y(t) ≤ φ(t, φ
0
) where
φ(t, φ
0
) is the solution of
˙
φ = L(1 + φ)
2
satisfying φ(t, φ
0
) = φ
0
.

DRAFT
EVENT-TRIGGERED REAL-TIME SCHEDULING OF STA BILIZING CONTROL TASKS 5
Assume now that ∆ = 0. Then, the inter-execution times are bounded by the time it takes for φ to evolve
from 0 to 1/P , that is, the inter-execution times are bounded by the solution τ ∈ R
+
of φ(τ, 0) = 1/P . Since
φ(τ, 0) = τL/(τL − 1) we obtain τ = 1/(L + LP ).
For ∆ > 0 we need a more detailed analysis. First, pick σ
0
satisfying σ < σ
0
< 1 (take for example σ
0
= σ+(1−
σ)/2) and le t P
0
be the Lipschitz constant for α
−1
(γ(|e|)/σ
0
). Let now ε
1
∈ R
+
satisfy φ(ε
1
, 1/P ) = 1/P
0
. Such
ε
1
always exists since φ is continuous,
˙
φ > 0 and 1/P < 1/P
0
. Then, by executing the control task at time t
i
,
defined by P |e| = |x|, we guarantee that for t ∈ [t
i
, t
i
+ε
1
[ we have |e| ≤ |x|/P
0
and thus also γ(|e|) ≤ σ
0
α(|x|).
Since σ
0
< 1 asymptotic stability is still guaranteed. The inter-execution times are now bounded by ∆ + τ
where τ is the time it takes for φ to evolve from |e(t
i
+ ∆)|/|x(t
i
+ ∆)| = |x(t
i
) − x(t
i
+ ∆)|/|x(t
i
+ ∆)|
to 1/P . We thus need to pick ∆ small enough so that |e(t
i
+ ∆)|/|x(t
i
+ ∆)| < 1/P since
˙
φ > 0. It now
follows from continuity
3
of |x(t
i
) − x(t
i
+ ∆)|/|x(t
i
+ ∆)| with respect to ∆ the existence of ε
2
> 0 such that
for any 0 ≤ ∆ ≤ ε
2
we have |x(t
i
) − x(t
i
+ ∆)|/|x(t
i
+ ∆)| < 1/P . The proof is now finished by taking
ε = min{ε
1
, ε
2
}.
Theorem 3.1 shows that the simple execution rule (2.9) results in a sequence of inter-execution times for the
control task that is guaranteed to be lower bounded provided that ∆ is sufficiently small. The techniques
used in the proof rely of Lipschitz continuity and are necessarily conservative for general nonlinear systems.
However, for linear systems they provide reasonable estimates and we can even provide computable bounds
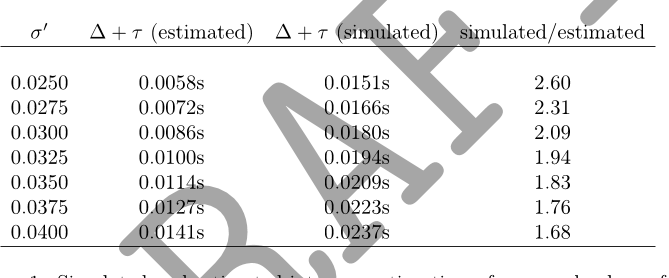
for ∆ as discussed in the next section.
4. The linear case
In this se ction we discuss the linear case in some detail since the arguments in the proof of Theorem can be
refined in order to provide a computational estimate for τ. We thus assume the control system to be of the
form:
˙x = Ax + Bu, x ∈ R
n
, u ∈ R
m
with A and B matrices of appropriate dimensions. We also assume the existence of a linear feedback:
u = Kx
rendering the closed loop system globally asymptotically stable and where K is a matrix of appropriate
dimensions. Note that in the linear case any such K renders the closed loop system ISS with respect to
measurement errors. We thus have a Lyapunov function V : R
n
→ R
+
0
satisfying:
a
|x|
2
≤ V (x) ≤ a|x|
2
(4.1)
∂V
∂x
(Ax + BKx + BKe) ≤ −a|x|
2
+ g|e||x|(4.2)
with a, a, a, g ∈ R
+
.
Corollary 4.1. Let ˙x = Ax + Bu be a linear control system, let u = Kx be a linear control law rendering the
closed loop system globally asymptotically stable and assume that ∆ = 0. For any initial condition in R
n
the
inter-event times {t
i+1
− t
i
}
i∈N
implicitly defined by the execution rule:
|e| ≥ σ|x|
are lower bounded by the time τ satisfying:
(4.3) φ(τ, 0) = σ
where φ(t, φ
0
) is the solution of:
(4.4)
˙
φ = |A + BK| +
|A + BK| + |BK|
φ + |BK|φ
2
3
Note that x(t
i
+ ∆) is never zero since the closed loop system converges asymptot ically to zero and thus never reaches zero
in finite time.