




Did you find this useful? Give us your feedback














8 citations
8 citations
...Localizing a minimal unsatisfiable subformula is necessary to determine the underlying reasons for the failure, and is used in many practical applications, including model checking on predicate abstraction[1], vacancy detection[2], error localization[3], and synthesizing circuits[4], etc....
[...]
8 citations
6 citations
6 citations
...Vacuity detection is concerned with avoiding tautologies and subformulas that are not relevant for the satisfaction of the formula (e.g., Simmonds et al. [20])....
[...]
[...]
7,392 citations
3,547 citations
2,424 citations
...In this section, we review bounded model-checking and resolution proofs....
[...]
...To determine whether K | k ϕ, the problem is converted to a propositional formula (see [4–6]) which is satisfiable if and only if there exists a length-k counterexample to K | k ϕ. is then given to a SAT solver which decides its satisfiability....
[...]
...More detailed definitions can be found in [4,7]....
[...]
...Below, we give an informal overview of Kripke structures, LTL formulas, and BMC....
[...]
...The BMC problem BMCk(K, ϕ) is to determine whether K satisfies ϕ for up to k steps, i.e., whether K | k ϕ....
[...]
1,456 citations
...More detailed definitions can be found in [4,7]....
[...]
1,377 citations
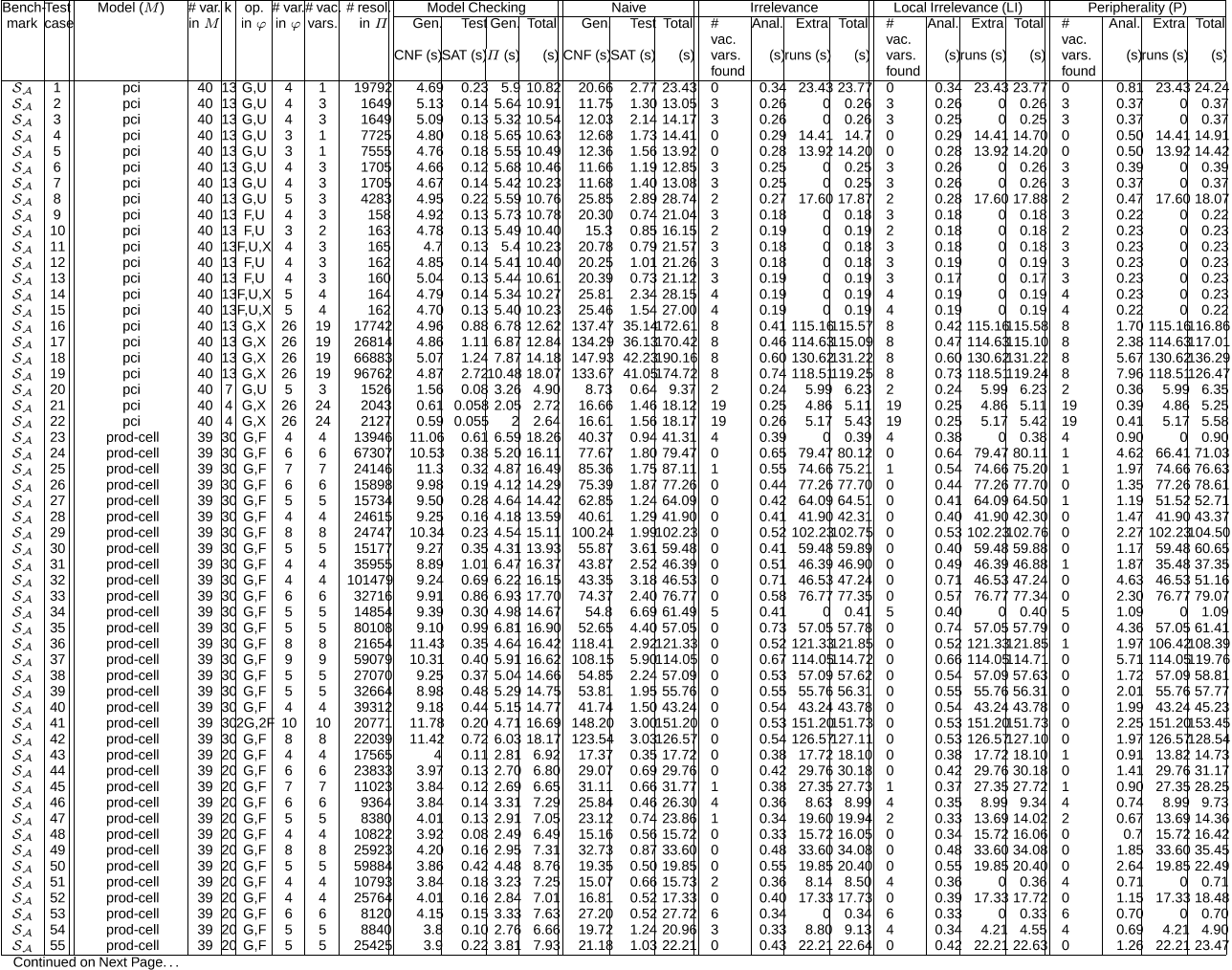
The authors plan to investigate this further in the future. The authors plan to enhance their methods by developing a heuristic based on the clause/variable ratio and proof size that indicates when naive detection should be applied instead. Thus, the authors believe that both local irrelevance and peripherality can be used to speed up naive detection.
Naive vacuity detection required eight model-checking runs, taking 115.68 seconds to generate the corresponding CNF theories and 2.36 seconds to test their satisfiability, requiring a total of 118.04 seconds.
The authors conjecture that the poor performance is due to a low clause/variable ratio [22] which favours naive detection in cases where vacuity is not present.
The error constraint CLe is encoded according to a recursive procedure which removes the temporal and logical operators from the property [4], e.g., the algorithm encodes ϕ =
Since the authors are interested in replacing expensive model-checking runs by inexpensive partial vacuity detection methods, the authors limit ourselves to considering the output of the original model-checking run on BMCk(K, ϕ), i.e., CLK ∪ CLe.
After the boolean formulas for the path and error constraints are calculated, they are converted to Conjunctive Normal Form (CNF) before being passed to a SAT solver.
If Π is a resolution proof whose root clauses are divided into two disjoint sets,A∪B, then the labeling functionL is defined recursively as shown in Figure 4, where c is used to represent a clause.
Armoni et al. [1] generalized the above syntactic definition of vacuity by introducing universal quantification, i.e., ∀x · ϕ[ψ ← x].
It might be possible to make them more effective by modifying the SAT solver to guide it to a particular kind of a proof (e.g., by changing the decision order heuristic), or to output multiple proofs (if possible).
In this context, a naive method for detecting vacuity is to replace subformulas of the temporal logic property with unconstrained boolean variables and run BMC for each such substitution.