Final-state effects on superfluid
4
He in the deep inelastic regime
F. Mazzanti
Departament d’Estructura i Constituents de la Mate
`
ria, Diagonal 645, Universitat de Barcelona, E-08028 Barcelona, Spain
J. Boronat
Departament de Fı
´
sica i Enginyeria Nuclear, Campus Nord B4-B5, Universitat Polite
`
cnica de Catalunya, E-08028 Barcelona, Spain
A. Polls
Departament d’Estructura i Constituents de la Mate
`
ria, Diagonal 645, Universitat de Barcelona, E-08028 Barcelona, Spain
~Received 3 August 1995 !
A study of final-state effects ~FSE! on the dynamic structure function of superfluid
4
He in the Gersch-
Rodriguez formalism is presented. The main ingredients needed in the calculation are the momentum distri-
bution and the semidiagonal two-body density matrix. The influence of these ground-state quantities on the
FSE is analyzed. A variational form of
r
2
is used, even though simpler forms turn out to give accurate results
if properly chosen. Comparison to the experimental response at high momentum transfer is performed. The
predicted response is quite sensitive to slight variations on the value of the condensate fraction, the best
agreement with experiment being obtained with n
0
5 0.082. Sum rules of the FSE broadening function are also
derived and commented. Finally, it is shown that Gersch-Rodriguez theory produces results as accurate as those
coming from other more recent FSE theories.
I. INTRODUCTION
Deep inelastic neutron scattering ~DINS! has been exten-
sively applied to the study of quantum fluids, since Hohen-
berg and Platzman’s
1
proposal of using DINS to determine
the momentum distribution n(k) of helium atoms in super-
fluid
4
He. The determination of n(k) in quantum liquids is a
challenging problem of fundamental interest.
2
In fact, the
knowledge of n(k) provides very useful information to un-
derstand basic properties of the quantum nature of these sys-
tems as the Bose-Einstein condensation. At the same time,
the theoretical analysis of DINS probes and stimulates the
development of modern many-body techniques. These issues
have been the main motivations of a considerable amount of
measurements and theoretical work on liquid
4
He and other
quantum liquids.
3–17
The inelastic scattering of neutrons by liquid
4
He is de-
scribed by the double differential cross section
d
2
s
dVd
v
5 b
2
k
f
k
i
S
~
q,
v
!
, ~1!
where b is the scattering length, k
i
and k
f
are the initial and
final wave vectors of the scattered neutron, and q and
v
are
the momentum and energy transferred from the neutron to
the sample. The dynamics of the sample is entirely contained
in S(q,
v
), the dynamic structure factor, which is the Fourier
transform of the density-density correlation function.
18
At
sufficiently high momentum transfer, the scattering is en-
tirely due to single atoms and S(q,
v
) can be accurately de-
scribed by the impulse approximation ~IA!,
1
provided that
the interatomic potential does not have an infinite repulsive
core. In this regime, the kinetic energy of an atom recoiling
from a neutron collision is much larger than the potential
energy due to the interaction with the neighboring atoms, so
that collisions of the former with other atoms can be ne-
glected. The IA predicts a simple relation between S(q,
v
)
and n(k),
S
IA
~
q,
v
!
5
1
~
2
p
!
3
r
E
dk n
~
k
!
d
S
v
2
v
R
2
k–q
m
D
, ~2!
where
v
R
5 q
2
/2m is the free atom recoil frequency, m is the
mass of the
4
He atoms, and n(k) is the thermally averaged
occupation probability of the single particle state of momen-
tum k, which reduces to that of the ground state at T5 0. The
delta function in Eq. ~2! takes care of the momentum and
energy conservation in the scattering event between the neu-
tron and a single atom. Assuming S(q,
v
)5 S
IA
(q,
v
), the
momentum distribution n(k) can be extracted from Eq. ~2!
by simple differentiation. Notice that in the previous equa-
tion and henceforth \ is set to 1.
In isotropic systems, where n(k) depends only on the
modulus of k, it is useful to introduce the Compton profile
J
IA
~
Y
!
5
q
m
S
IA
~
q,
v
!
, ~3!
which is driven by a single variable
Y5
m
q
S
v
2
q
2
2m
D
, ~4!
and fulfills Y scaling.
19
If a finite fraction of atoms n
0
occu-
pies the zero momentum state, J
IA
(Y) presents a
d
peak of
strength n
0
at Y5 0. However, this expected signature of the
condensate is not observed in experiments performed at
momentum transfer as high as 23 Å
2 1
,
4
because the IA
spectrum is broadened by both final-state effects ~FSE! and
instrumental resolution effects ~IRE!. Hence the theoretical
interpretation of the experimental data requires not only the
PHYSICAL REVIEW B 1 MARCH 1996-IVOLUME 53, NUMBER 9
53
0163-1829/96/53~9!/5661~9!/$10.00 5661 © 1996 The American Physical Society

knowledge of n(k), but also an accurate description of both
the dynamics which determines FSE and the instrumental
broadening function.
5
Several methods to account for FSE have been
proposed.
8,9,12–15
Among them, we will focus on the so-
called convolutive theories, in which
S
~
q,
v
!
5
E
2 `
`
d
v
8
S
IA
~
q,
v
8
!
R
~
q,
v
2
v
8
!
, ~5!
where R(q,
v
) is the FSE broadening function.
After the first attempt
1
to approximate R(q,
v
)bya
Lorentzian of width proportional to the
4
He-
4
He cross sec-
tion, Gersch et al.
8
expressed the response function S(q,
v
)
ina1/qseries expansion, whose coefficients are given by
integrals of many-body correlation functions averaged on the
ground state of the system. In this approach, the response
when q→ ` is given by the first term of the expansion of the
incoherent part of S(q,
v
), which turns to be exactly the IA.
However, the theory could not deal with realistic interatomic
potentials presenting a strong repulsion at short distances. To
overcome this problem, Gersch and Rodriguez
9
proposed a
cumulant expansion of S(q,t) which provides an adequate
frame for calculating the response function at high momen-
tum transfer. The full calculation is impractical, but with
some approximations based on physical grounds, S(q,
v
)
can be expressed in terms of the one- and the semidiagonal
two-body density matrices, and the two-body interaction. At
the time the theory was proposed the numerical application
was made with a very simple approximation of the two-body
density matrix that resulted in an overestimation of the re-
sponse at the quasielastic peak.
10
The main purpose of the present work is to revisit Gersch-
Rodriguez theory, and show that using a realistic two-body
density matrix one gets a S(q,
v
) in good agreement with
both experimental data and more recent theories of FSE.
12,14
In the next section, a review of the theory is presented.
Section III is devoted to the discussion of the results and
their comparison with the experimental data. A sum rules
analysis of R(q,
v
) is presented in Sec. IV. In Sec. V our
results are compared with other FSE theories, and finally
Sec. VI summarizes the main conclusions of the work.
II. GERSCH-RODRIGUEZ THEORY OF FSE
In the Gersch-Rodriguez theory,
9
the density-density cor-
relation factor S(q,t) is expressed as the product of the IA
and the FSE correcting function by means of a cumulant
expansion. The nth order cumulant accounts for the correla-
tions among the struck atom and clusters of n particles in the
background. In the high momentum transfer limit, those
terms with n5 1 carry the most significant corrections. At
this level, the FSE broadening function can be expressed as a
function of the interatomic potential and the one- and two-
body density matrices.
The starting point in Gersch-Rodriguez theory is the time
representation of the response
NS
~
q,t
!
5
(
j,l
^
e
2iqr
l
e
iHt
e
iqr
j
e
2 iHt
&
5
(
j,l
^
e
iq
~
r
j
2r
l
!
e
2iqr
j
e
iHt
e
iqr
j
e
2 iHt
&
, ~6!
which can be brought to the following form:
NS
~
q,t
!
5e
i
v
q
t
(
j,l
K
e
iq
~
r
j
2r
l
!
e
iL
j
t
3Texp
F
i
E
0
t
dt
8
H
~
r
j
2v
q
t
8
!
G
e
2iHt
L
, ~7!
where T is the time-ordering operator and H(r
j
2 v
q
t
8
) is the
actual Hamiltonian of the system where the position coordi-
nate of particle j has been shifted by an amount v
q
t
8
. As the
interatomic potential considered is velocity independent, one
can write
H
~
r
j
2 v
q
t
8
!
5 H1 U
j
~
v
q
t
8
!
, ~8!
with
H5
(
j
p
j
2
2m
1
(
i, j
V
~
r
ij
!
~9!
and
U
j
~
v
q
t
8
!
5
(
mÞ j
U
j,m
~v
q
t
8
!
,
U
j,m
~v
q
t
8
!
5
@
V
~
r
j
2 v
q
t
8
,r
m
!
2 V
~
r
j
,r
m
!
#
, ~10!
where
v
q
5 q/m and
v
q
5 q
2
/2m.
The incoherent part of the response, which is defined by
taking particles labeled j and l in Eq. ~7! to be the same, is
the only contribution at large q. In this limit, S(q,t) may be
written in the following way:
S
~
q,t
!
5 e
i
v
q
t
K
e
iv
q
tp
1
e
iHt
Texp
F
i
E
0
t
dt
8
(
mÞ1
U
ˆ
1,m
~
v
q
t
8
!
G
e
2 iHt
L
,
~11!
where U
ˆ
(v
q
t
8
) is the previously defined potential operator
but with the position operators evaluated at time t
8
rather
than at t5 0. Notice that expression ~11! is as hard to evalu-
ate as the original S(q,t). An exact treatment would require
the knowledge of the time evolution of the whole system, so
different approximations should be made in order to deal
with this last relation.
Gersch and Rodriguez
9
performed a cumulant expansion
of the ground-state expectation value of Eq. ~11!. The expan-
sion contains an infinite number of terms, and allows for the
factorization of the IA from the total response
S
~
q,t
!
5 S
IA
~
q,t
!
R
~
q,t
!
, ~12!
R(q,t) being the FSE correcting function given by
5662 53F. MAZZANTI, J. BORONAT, AND A. POLLS

R
~
q,t
!
5 exp
F
2
1
^
e
itv
q
p
1
&
(
mÞ1
K
e
itv
q
p
1
3
F
12Texp
H
i
E
0
t
dt
8
U
ˆ
1,m
~
v
q
t
8
!
J
G
L
1 •••
G
. ~13!
Up to this point, the result is exact because it is nothing
more than a rearrangement of the different terms entering in
S(q,t). The first problem in the calculation of Eq. ~13! is
associated to the infinite number of terms appearing in the
exponential. Such a difficulty can be skipped if one looks for
the underlying physics contained in each term: the contribu-
tion of the nth order cumulant to S(q,t) accounts for the
correlations between n-particle clusters during their interac-
tions with the struck atom. One may expect that the first
significant correction to the IA is produced by the multiple
scattering of the struck particle with the atoms of the media,
considering them independently of each other. This corre-
sponds to a truncation of the series beyond the first order
cumulant.
The second problem lies on the evaluation of the time
dependence appearing in the particle coordinates of
U
ˆ
1,m
(v
q
t
8
). In the large q limit, the displacement of the
struck particle is much larger than the average movement of
the background atoms. Thus one can discard the time depen-
dence of r(t)inU
ˆ
1,m
. This is a safe procedure as, even
though the inclusion of such a time dependence avoids hard-
core collisions between the struck particle and other target
atoms, the contribution to R(q,t) coming from those situa-
tions vanishes due to rapid oscillations in the imaginary ex-
ponential of Eq. ~13!. Therefore, one can write
9
R
~
q,t
!
5 exp
F
2
1
r
1
~v
q
t
!
E
dr
r
2
~
r,0;r1 v
q
t,0
!
F
1
2 exp
H
i
E
0
t
dt
8
$
V
@
r1v
q
~
t2t
8
!
#
2V
@
r1v
q
t
#
%
J
GG
,
~14!
where
r
1
and
r
2
are the one-body and semidiagonal two-
body density matrices of the system, respectively. R(q,t)isa
complex function, but its Fourier transform is real because
its real part is even and its imaginary part odd under the
change t→ 2 t.
Equation ~12! predicts S(q,t) as the product of S
IA
(q,t)
and R(q,t), and therefore S(q,
v
) is the convolution of
S
IA
(q,
v
) and R(q,
v
)
S
~
q,
v
!
5
E
2 `
`
d
v
8
S
IA
~
q,
v
8
!
R
~
q,
v
2
v
8
!
. ~15!
In the particular case of liquid
4
He, the momentum dis-
tribution n(k) may be written as
n
~
k
!
5
~
2
p
!
3
r
n
0
d
~
k
!
1 n
˜
~
k
!
, ~16!
where n
0
is the condensate fraction value and n
˜
(k) stands for
the occupation of nonzero momentum states. Consequently,
S
IA
(q,
v
) is split in two parts
S
IA
~
q,
v
!
5 n
0
d
S
v
2
q
2
2m
D
1
m
4
p
2
r
q
E
u
m
v
q
2
q
2
u
`
kn
~
k
!
dk
5n
0
d
S
v
2
q
2
2m
D
1S
˜
IA
~
q,
v
!
, ~17!
where the first term on the right-hand side is the condensate
response which appears as a delta peak of strength n
0
located
at the quasielastic energy, and S
˜
IA
(q,
v
) is the noncondensate
contribution of n(k) to the IA. Introducing the West variable
Y5 m
v
/q2 q/2, S
IA
(q,
v
) can be expressed in terms of the
Compton profile
q
m
S
IA
~
q,
v
!
[J
IA
~
Y
!
5 n
0
d
~
Y
!
1
1
4
p
2
r
E
u
Y
u
`
kn
~
k
!
dk,
~18!
which scales in Y.
Moreover, at high q the response is usually expressed in
terms of Y through the relation
J
~
q,Y
!
5
q
m
S
~
q,
v
!
, ~19!
and thus Eq. ~15! is transformed into
J
~
q,Y
!
5
E
2 `
`
dY
8
J
IA
~
Y
8
!
R
~
q,Y2 Y
8
!
5 n
0
R
~
q,Y
!
1
E
2 `
`
dY
8
J
˜
IA
~
Y
8
!
R
~
q,Y2 Y
8
!
,
~20!
where
R
~
q,Y
!
5
q
m
R
~
q,
v
!
. ~21!
III. NUMERICAL RESULTS
In this section, we present results for the FSE correcting
function R(q,Y) and the response function J(q,Y) calcu-
lated in the framework of the Gersch-Rodriguez formalism.
The input density matrices
r
1
(r) and
r
2
(r
1
,r
2
;r
1
8
,r
2
) used to
calculate J
IA
(Y) and R(q,Y) have been obtained in the
framework of the HNC theory
20,21,23
from a variational
many-body wave function containing two- and three-body
correlations.
22
The variational minimization has been per-
formed for the HFDHE2 Aziz potential
24
at the experimental
equilibrium density (
r
5 0.365
s
2 3
;
s
5 2.556 Å!. The
ground-state description obtained with this wave function is
in good agreement with recent Green’s function Monte Carlo
calculations.
25,26
The discussion is separated in two parts, the
first one being devoted to the study of both R(q,Y) and
J(q,Y) and their comparison to experimental data, and the
second one to the analysis of the dependence of these func-
tions on the different approximations used in the variational
description of the ground-state wave function.
The actual calculation of the FSE broadening function is
initially performed in time representation ~14!. R(q,x)isa
complex quantity which can be written in the following way:
53 5663
FINAL-STATE EFFECTS ON SUPERFLUID
4
He IN THE . . .

R
~
q,x
!
5 e
f
~
q,x
!
@
cos„
c
~
q,x
!
…1 i sin„
c
~
q,x
!
…
#
, ~22!
with
f
~
q,x
!
52
2
r
1
~
x
!
E
dr
r
2
~
r,0;r1x
!
3sin
2
F
1
2
v
q
E
0
x
du
$
V
~
r1x2u
!
2V
~
r1x
!
%
G
,
c
~
q,x
!
5
1
r
1
~
x
!
E
dr
r
2
~
r,0;r1x
!
3sin
F
1
v
q
E
0
x
du
$
V
~
r1x2u
!
2V
~
r1x
!
%
G
,
~23!
x being
v
q
t. As can be seen from Eq. ~23!,
f
(q,x) and
c
(q,x) are even and odd functions of x, respectively. There-
fore, the real and imaginary parts of R(q,x) are respectively
even and odd under the change x→ 2 x, and consequently
R(q,Y) is real. Even if the potential becomes very repulsive
at short distances, as is the case of the Aziz potential, Eq.
~14! gives an R(q,Y) which does not diverge.
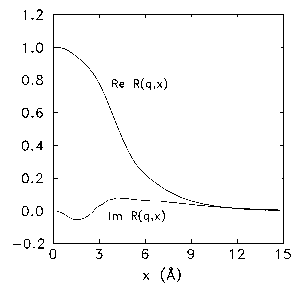
The real and imaginary parts of R(q,x) are shown in Fig.
1 for q5 23.1 Å
2 1
. In the relevant range of x,ReR(q,x) has
a dominant decreasing behavior. The ReR(q,x) and Im-
R(q,x) are related to the symmetric and antisymmetric com-
ponents of R(q,Y), respectively. As the imaginary part is
much smaller than the real part, R(q,Y) is mostly symmetric
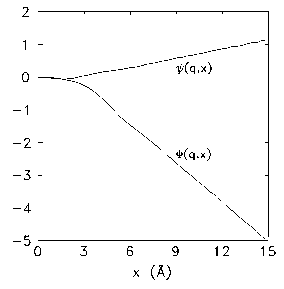
around Y5 0. In Fig. 2, we show
c
(q,x) and
f
(q,x)at
q523.1 Å
2 1
.
f
(q,x) is a negative and a monotonously de-
creasing function of x, causing both the real and the imagi-
nary parts of R(q,x) tend to zero when x→ `~22!.
In Fig. 3, we show R(q,Y) at two different values of q,
23.1 Å
2 1
and 15.0 Å
2 1
. The main trends of R(q,Y) in all
FSE convolution theories are the same: a dominant central
peak and small oscillating tails which vanish as
u
Y
u
in-
creases. As one can see, the shape of R(q,Y) smoothly
changes with q, this variation being reflected in an overall
redistribution of the strength between the main peak and the
wings. When q increases, the peak appears higher and nar-
rower pointing to the tendency of R(q,Y) to become a delta
distribution in the limit q→ `.
The existence of a finite condensate fraction n
0
in super-
fluid
4
He plays an important role in the FSE corrections, as
is reflected in Fig. 4 where the broadening of the condensate
and noncondensate parts of J
IA
(Y) are separately shown.
The small differences between J
˜
IA
(Y) ~dotted line! and the
convolution of J
˜
IA
(Y) with R(q,Y) ~long-dashed line! reveal
small FSE on the noncondensate part of the response at high
q. In contrast, the broadening of the condensate term ~short-
dashed line!, i.e., the convolution product of R(q,Y) and
n
0
d
(Y), contributes to J(q,Y)asn
0
R(q,Y) which is a func-
tion with an appreciable width and height. The inclusion of
the latter term produces a total J(q,Y) ~solid line! which
FIG. 1. Real and imaginary parts of R(q,x)atq523.1 Å
2 1
.
FIG. 2. Functions
f
(q,x) and
c
(q,x)atq523.1 Å
2 1
.
FIG. 3. R(q,Y)atq523.1 Å
2 1
~solid line! and q5 15.0 Å
2 1
~dashed line!.
FIG. 4. Different contributions to J(q,Y)atq523.1 Å
2 1
. Dot-
ted line, noncondensate term of J
IA
(Y); long-dashed line, noncon-
densate term of J
IA
(Y) after the convolution with R(q,Y); short–
dashed line, condensate contribution once broadened by FSE; solid
line, total response.
5664 53
F. MAZZANTI, J. BORONAT, AND A. POLLS
manifests a sizeable departure from the IA prediction. There-
fore, FSE corrections in superfluid
4
He appear to be relevant
even at so high q’s.
12
A direct comparison between theoretical and experimental
dynamic structure factors is not possible due to the presence
of instrumental resolution effects ~IRE! in the experimental
data acquisition process. It would be desirable, from a theo-
retical viewpoint, to remove the IRE inherent to the mea-
sured response, especially at high q where they become
larger. However, the latter is an ill-posed problem due to the
statistical noise of the data, and thus the only way to com-
pare theory and experiment is by convoluting the theoretical
J(q,Y) with an instrumental resolution function I(q,Y). At
present, I(q,Y) is obtained from a Monte Carlo simulation
of the experimental setup, and in contrast to earlier models
used in neutron scattering analysis, it is neither Gaussian nor
symmetric around Y5 0, and is comparable in width and
height to R(q,Y) at those momenta.
4
The influence of
I(q,Y) in the response is sketched in Fig. 5 for q5 23.1
Å
2 1
. As one can see, the introduction of the IRE in the
response ~solid line! appreciably modifies J(q,Y) ~dashed
line!. The most important effect of I(q,Y) is to quench the
central peak reducing the effects of the FSE correction on
J
IA
(Y), whereas the tails remain almost unchanged.
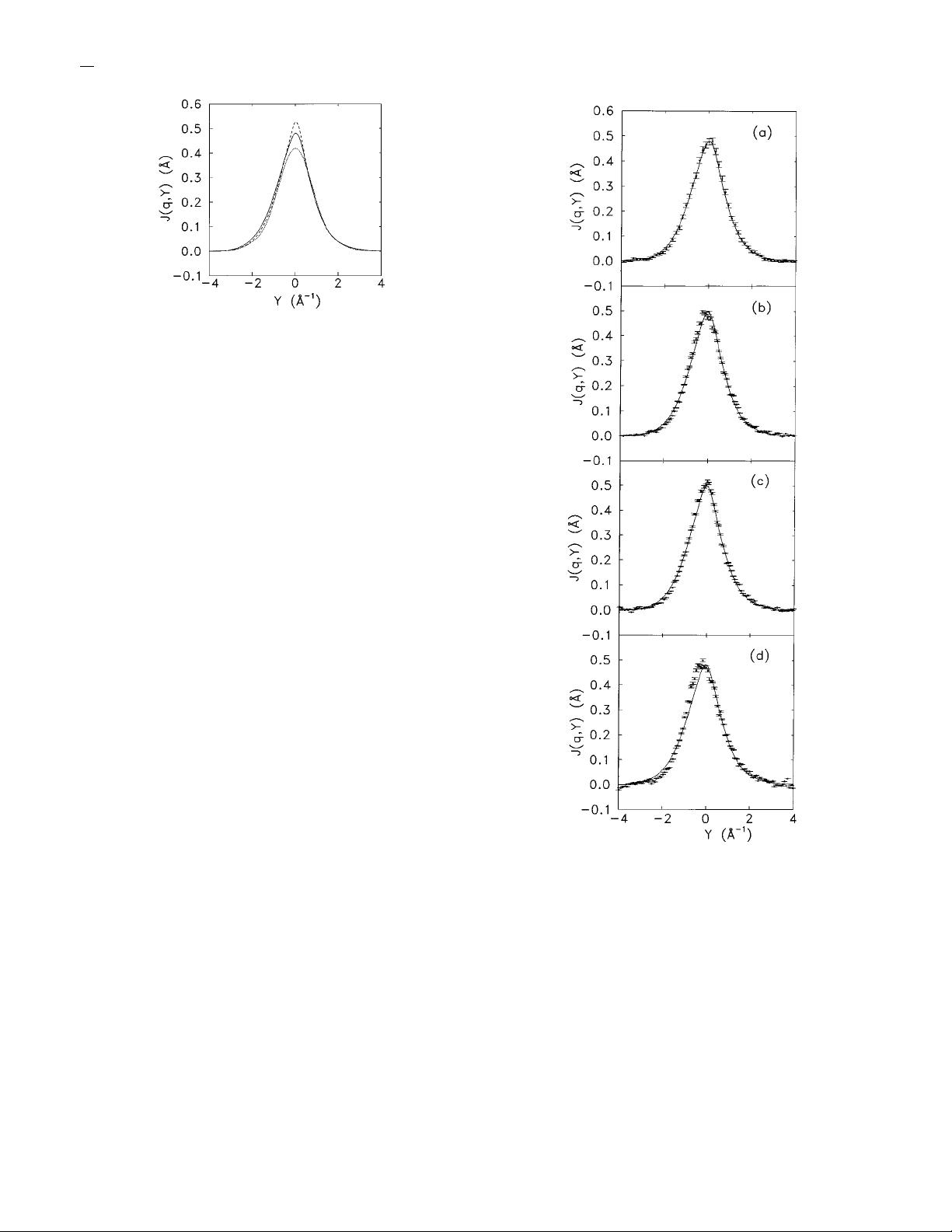
In Fig. 6, we present results of J(q,Y) broadened by the
IRE at different values of q in comparison with inelastic
scattering data at T5 0.34 K from Ref. 4. There is an overall
agreement between the predicted and the observed scattering
data, the quality of the Gersch-Rodriguez theory being com-
parable to results provided by other theories
12,14
~see also
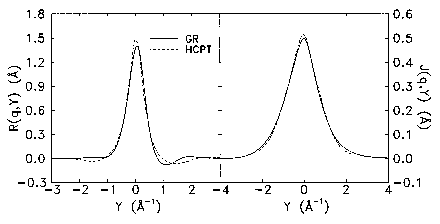
Sec. V!. It is worth to notice that all FSE theories are stressed
when applied to intermediate q values. This is also apparent
in our results, as one can see for the lowest q value reported
in Fig. 6. Thus, whereas the experimental peak shifts its lo-
cation to a small negative Y value, the theoretical one is
shifted to so small positive values of Y that it is not appre-
ciable in the figure.
The most relevant quantity in the calculation of J(q,Y)is
the momentum distribution n(k) which completely deter-
mines the Compton profile J
IA
(Y). The influence of n(k)in
J(q,Y) is shown in Fig. 7. The dashed and solid lines corre-
spond to a Jastrow n(k)
@
n
J
(k)# and a Jastrow plus triplet
n(k)
@
n
JT
(k)#, respectively. The condensate fraction pre-
dicted by the two approximations are slightly different,
n
0
J
5 0.091 and n
0
JT
50.082. This reduction of n
0
produces a
small decrease of strength in the peak of J(q,Y) bringing our
theoretical prediction closer to the experiment. A basic ingre-
dient in the calculation of R(q,Y) is the semidiagonal two-
body density matrix, which in the framework of the HNC
theory is given by
23
r
2
~
r
1
,r
2
;r
8
1
,r
2
!
5
rr
1
~
r
11
8
!
g
wd
~
r
12
!
g
wd
~
r
1
8
2
!
exp
@
A
~
r
1
,r
2
;r
8
1
!
#
, ~24!
where
r
1
(r
11
8
) is the one-body density matrix, g
wd
(r)isan
auxiliary two-body radial distribution function, and
FIG. 5. Effects of the different broadenings to the response at
q5 23.1 Å
2 1
. Dotted line, noncondensate IA prediction; dashed
line, IA broadened by FSE; solid line, total J(q,Y) including both
FSE and IRE.
FIG. 6. Comparison of the predicted J(q,Y)at~a!23.1 Å
2 1
,
~b! 17.9 Å
2 1
, ~c! 15.0 Å
2 1
, and ~d! 10.2 Å
2 1
with experimental
data ~points with error bars!.
53
5665
FINAL-STATE EFFECTS ON SUPERFLUID
4
He IN THE . . .