scispace - formally typeset
Search or ask a question
Journal Article•DOI•

Flexible Class of Skew‐Symmetric Distributions

Yanyuan Ma1, Marc G. Genton1•
North Carolina State University1
01 Sep 2004-Scandinavian Journal of Statistics (Blackwell)-Vol. 31, Iss: 3, pp 459-468
TL;DR: In this paper, a flexible class of skew-symmetric distributions for which the probab- ility density function has the form of a product of a symmetric density and a skewing function is proposed.
Abstract: We propose a flexible class of skew-symmetric distributions for which the probab- ility density function has the form of a product of a symmetric density and a skewing function. By constructing an enumerable dense subset of skewing functions on a compact set, we are able to consider a family of distributions, which can capture skewness, heavy tails and multimodality systematically. We present three illustrative examples for the fibreglass data, the simulated data from a mixture of two normal distributions and the Swiss bills dlata.
Figures (4)

Content maybe subject to copyright    Report

A Flexible Class of Skew-Symmetri Distributions
(running head: exible skew-symmetri distributions)
YANYUAN MA
North Carolina State University
MARC G. GENTON
North Carolina State University
ABSTRACT. We prop ose a exible lass of skew-symmetri distributions for whih the
probability density funtion has the form of a pro dut of a symmetri density and a skewing
funtion. By onstruting an enumerable dense subset of skewing funtions on a ompat
set, we are able to onsider a family of distributions whih an apture skewness, heavy
tails, and multimo dality systematially. We present three illustrative examples for the
b er-glass data, simulated data from a mixture of two normal distributions, and Swiss
bills data.
Key Words:
dense subset; generalized skew-elliptial; multimodality; skewness; skew-normal.
1 Intro dution
A popular approah to ahieve departures from normality onsists of modifying the probability density
funtion (p df ) of a random vetor in a multipliative fashion. Wang, Boyer, & Genton (2004) showed
that any
p
-dimensional multivariate pdf
g
(
x
) admits, for any xed loation parameter
2
R
p
, a unique
skew-symmetri (SS) representation:
g
(
x
) = 2
f
(
x
)
(
x
)
;
(1)
where
f
:
R
p
!
R
+
is a symmetri p df and
:
R
p
!
[0
;
1℄ is a skewing funtion satisfying
(
x
) =
1
(
x
). Vie-versa, any funtion
g
of the type dened by (1) is a valid pdf. By symmetri, we mean
f
(
x
) =
f
(
x
) and we will use \symmetri pdf " and the prop erty
f
(
x
) =
f
(
x
) interhangeably in
the sequel. Throughout this pap er, we restrit our interest on funtions
f
2
C
0
(
R
p
) and ontinuous
skewing funtions
(
x
), where
C
0
(
R
p
) denotes ontinuous funtions on
R
p
with the prop erty
f
(
x
)
!
0
when
k
x
k
2
! 1
, and
k k
2
denotes the
L
2
norm. Genton & Lop erdo (2002) onsidered the subfamily
of generalized skew-elliptial (GSE) distributions for whih the p df
f
in (1) is elliptially ontoured
rather than only symmetri. Many denitions of skewed distributions found in the literature an be
written in the form of a skew-symmetri distribution (1). For instane, Azzalini & Dalla Valle's (1996)
multivariate skew-normal distribution orresp onds to
f
(
x
) =
p
(
x
;
0
;
) and
(
x
) = (
T
x
), where
p
(
x
;
;
) is the
p
-dimensional multivariate normal pdf with mean vetor
and orrelation matrix ,
1
is the standard normal umulative distribution funtion (df ), and
is a shap e parameter ontrolling
skewness. Similarly, multivariate distributions suh as skew-
t
(Brano & Dey, 2001; Azzalini & Capitanio,
2003; Jones & Faddy, 2003; Sahu, Brano, & Dey, 2003), skew-Cauhy (Arnold & Beaver, 2000) and
other skew-elliptial ones (Azzalini & Capitanio, 1999; Brano & Dey, 2001; Sahu
et al.
, 2003) an be
represented by the skew-symmetri distribution (1) with appropriate hoies of
f
and
.
In this artile, we prop ose a exible lass of distributions (1) by onstruting an enumerable dense
subset of the skewing funtions
on a ompat set. The result is a family of distributions whih
an apture skewness, heavy tails, and multimodality systematially. The onstrution of the subset is
through p olynomials, whih has a similar avor as the seminonparametri (SNP) representation prop osed
by Gallant & Nyhka (1987). The latter is dened as the pro dut of the standard normal p df and the
square of a polynomial. The SNP distribution requires the oeÆients in the polynomial to b e onstrained
in order to yield a valid density. It also relies on rejetion sampling shemes to simulate random samples.
These diÆulties do not o ur with our onstrution.
The ontent of the pap er is organized as follows. In Setion 2, we desribe a subset of skewing
funtions based on o dd p olynomials and prove that it results in a dense subset of the skew-symmetri
distributions. In partiular, we dene exible skew-normal and skew-
t
distributions that an have more
than one mode. This is an essential property for some situations and provides an alternative to modeling
with mixtures of distributions. The exibility and p ossible multimodality of the new lass of distributions
is illustrated in Setion 3. We present three illustrative examples in Setion 4, and a disussion in Setion
5.
2 A dense subset of skew-symmetri distributions
In this setion, we onstrut a dense subset of skew-symmetri distributions through approximating the
skewing funtion
on a ompat set. Any ontinuous skewing funtion
an be written as:
(
x
) =
H
(
w
(
x
))
;
(2)
where
H
:
R
!
[0
;
1℄ is the df of a ontinuous random variable symmetri around 0, and
w
:
R
p
!
R
is an o dd ontinuous funtion, that is
w
(
x
) =
w
(
x
). In fat, for a hosen
H
suh that
H
1
exists,
w
(
x
) =
H
1
(
(
x
)) is a ontinuous odd funtion. This representation has been used by Azzalini &
Capitanio (2003) to dene ertain distributions by p erturbation of symmetry. Note however that the
representation (2) is not unique due to the many possible hoies of
H
.
Let
P
K
(
x
) b e an o dd p olynomial of order
K
. A p olynomial of order
K
in
R
p
is dened as a linear
ombination of terms of the form
Q
p
i
=1
x
r
i
i
, where
k
=
P
p
i
=1
r
i
K
. If eah term has an odd order (all
k
's are o dd), then the polynomial is alled an odd p olynomial, whereas if eah term has an even order
(all
k
's are even), it is alled an even polynomial. We dene exible skew-symmetri (FSS) distributions
2
by restriting (1) to:
2
f
(
x
)
K
(
x
)
;
(3)
where
K
(
x
) =
H
(
P
K
(
x
)) and
H
is any df of a ontinuous random variable symmetri around 0. Note
that there are no onstraints on the oeÆients of the p olynomial
P
K
in order to make (3) a valid
pdf. In partiular, (3) denes exible generalized skew-elliptial (FGSE) distributions when the pdf
f
is
elliptially ontoured. For instane, exible generalized skew-normal (FGSN) distributions are dened
by:
2
p
(
x
;
;
)(
P
K
(
A
(
x
)))
;
(4)
and exible generalized skew-
t
(FGST) distributions are dened by:
2
t
p
(
x
;
;
;
)
T
(
P
K
(
A
(
x
));
)
;
(5)
where we use the Choleski deomposition
1
=
A
T
A
,
t
p
denotes a
p
-dimensional multivariate
t
pdf,
and
T
denotes a univariate
t
df, both with degrees of freedom
. Note that we ould use , or any
other symmetri df, instead of
T
for the skewing funtion in (5). In pratie, a popular hoie for the
df
H
would b e or the univariate df orresponding to the symmetri p df
f
. Eetively, the following
proposition shows that FSS distributions an approximate skew-symmetri distributions arbitrarily well.
Prop osition 1
Let the lass of exible skew-symmetri (FSS) distributions onsist of distributions with
pdf given in (3) and the lass of skew-symmetri (SS) distributions of distributions with pdf given in (1),
where
f
2
C
0
(
R
p
)
in both lasses and
is ontinuous. Then the lass of FSS distributions is dense in
the lass of SS distributions under the
L
1
norm.
Pro of
: An arbitrary distribution in the SS lass an be written as 2
f
(
x
)
H
(
w
(
x
)), where
f
and
H
are ontinuous,
H
1
exists, and
w
is a ontinuous o dd funtion. Beause
f
2
C
0
(
R
p
), for any arbitrary
>
0, we an nd a ompat set
D
whih is symmetri around
(if
x
2
D
then
x
2
D
), suh that
for any
x
=
2
D
,
f
(
x
)
< =
4. Thus, for any
x
=
2
D
,
j
2
f
(
x
)
(
x
)
2
f
(
x
)
H
(
P
((
x
))
j
<
for any odd p olynomial
P
.
Sine
f
is ontinuous,
f
is bounded on
D
. We denote the bound by
C
, i.e.
f
(
x
)
C
for any
x
2
D
. We use
D
1
to denote the image spae of
w
, i.e.
D
1
=
f
w
(
x
)
j
x
2
D
g
. Beause of the
ontinuity of
w
, whih is a result of the ontinuity of b oth
H
and
,
D
1
is also ompat. The ontinuous
funtion
H
is uniformly ontinuous on the ompat set
D
1
. Hene there exists
>
0 suh that for
any
y
1
,
y
2
2
D
1
and
j
y
1
y
2
j
<
, we get
j
H
(
y
1
)
H
(
y
2
)
j
< =
(2
C
). From the Stone-Weierstrass
theorem (see e.g. Rudin, 1973, p. 115), there exists a polynomial
P
suh that
j
w
(
x
)
P
(
x
)
j
<
for any
x
2
D
. We deomp ose
P
into an even term
P
e
and an odd term
P
o
, i.e.
P
=
P
e
+
P
o
.
Then
j
w
(
x
)
P
e
(
x
)
P
o
(
x
)
j
<
and
j
w
(
x
)
P
e
(
x
)
P
o
(
x
)
j
<
. Beause
w
and
P
o
are odd, and
P
e
is even, we get
j
w
(
x
)
P
e
(
x
) +
P
o
(
x
)
j
<
. Notie that
2
j
w
(
x
)
P
o
(
x
)
j j
w
(
x
)
P
e
(
x
)
P
o
(
x
)
j
+
j
w
(
x
)
P
e
(
x
) +
P
o
(
x
)
j
<
2
,
3
so
j
w
(
x
)
P
o
(
x
)
j
<
. Combining these results, we know that for an arbitrary member
2
f
(
x
)
H
(
w
(
x
)) in SS and an arbitrary
>
0, we an nd a member 2
f
(
x
)
H
(
P
o
(
x
)) in
FSS suh that
j
2
f
(
x
)
H
(
w
(
x
))
2
f
(
x
)
H
(
P
o
(
x
))
j
<
for any
x
2
D
.
Hene FSS is dense in SS with resp et to the
L
1
norm.
Remark 1
The requirement
f
2
C
0
(
R
p
)
in proposition 1 an be relaxed to al low that
f
has a nite
number,
m
say, of poles. In this ase, FSS is dense in SS with respet to almost uniform onvergene
(uniform in a set whose omplement is of measure arbitrarily smal l). Indeed, let
R
p
(
r
)
denote
R
p
minus
the union of
m
open bal ls of radius
r
entered at the
m
poles. Then FSS is dense in SS on
R
p
(
r
)
under
the
L
1
norm. Letting
r
!
0
, the result fol lows.
Proposition 1 shows in partiular that the lass of generalized skew-elliptial, skew
t
, and skew-
normal distributions an b e approximated arbitrarily well by their exible versions.
3 Flexibility and multimodality
In Figure 1, we illustrate the shap e exibility of the FGSN distribution in the univariate ase. Its pdf
for
K
= 3 is dened by:
2
1
(
x
;
;
2
)(
(
x
)
=
+
(
x
)
3
=
3
)
:
(6)
Figure 1 should b e here.
Figure 1(a) depits the p df of the FGSN model for
= 0,
2
= 1,
= 4, and
= 0, i.e. it redues
to Azzalini's (1985) univariate skew-normal distribution. However, when
6
= 0, the p df (6) an exhibit
bimodality as shown in Figure 1(b) with
= 1, and
=
1. In general, as the degree
K
of the o dd
polynomial in the skewing funtion beomes large, the number of mo des allowed in the p df inreases,
thus induing a greater exibility in the available shapes. Unfortunately, the number of modes depends
on the degree
K
of the o dd p olynomial, on the symmetri pdf
f
, and on the df
H
of the skewing
funtion
K
in a omplex fashion. Indeed, even for the univariate situation given by
p
= 1, the mo des
are determined by zeros of the rst derivative of the FSS distribution (3) given by:
2
f
0
(
x
)
H
(
P
K
(
x
)) + 2
f
(
x
)
H
0
(
P
K
(
x
))
P
0
K
(
x
)
;
(7)
for whih the number of zeros annot b e easily omputed. Even with restritions to some sp ei
f
and
H
funtions, a general statement on the relation between the number of mo des and the order of the
polynomial seems not available. However, in the univariate ase, if we onsider a normal pdf
f
=
1
and
a standard normal df
H
= with an o dd p olynomial of order
K
= 3, we have the following proposition.
Prop osition 2
The lass of exible generalized skew-normal (FGSN) distributions with pdf
2
1
(
x
;
;
2
)(
(
x
)
=
+
(
x
)
3
=
3
)
has at most 2 modes.
4
Pro of
: Without loss of generality, we an set
= 0,
= 1, assume
>
0, and only need to prove that
(
x
) = 2
(
x
)(
x
+
x
3
) has at most two modes. We prove this by ontradition. If
(
x
) has more
than two mo des, then
0
(
x
) has at least ve zeros. In the following pro of, we show that this annot b e
the ase. We have
0
(
x
) = 2
(
x
)((
+ 3
x
2
)
(
x
+
x
3
)
x
(
x
+
x
3
)) and need to onsider three
ases:
ase 1:
= 0
We write
0
(
x
) = 2
x
(
x
)
(
x
), where
(
x
) = 3
x
(
x
3
)
(
x
3
). We an verify that
0
(
x
) =
3
(
x
3
)
1
(
y
) where
y
=
x
2
and
1
(
y
) = 1
y
3
2
y
3
. Sine
1
(
y
) is a dereasing funtion on
y
0,
0
(
x
) has at most two zeros. Thus,
(
x
) has at most three zeros, hene
0
(
x
) has at most four
zeros.
ase 2:
>
0
Notie that
0
(
x
)
>
0 for
x
0. For
1
(
x
) =
0
(
x
)
=
(2
x
(
x
)) =
(
x
+
x
3
)(
+ 3
x
2
)
=x
(
x
+
x
3
),
we get
0
1
(
x
) =
(
x
+
x
3
)
=
(
9
x
2
)
2
(
y
), where
y
=
+ 3
x
2
>
0 and
2
(
y
) =
y
4
+
y
3
+ (3
2
2
)
y
2
(3
+ 9
)
y
+ 18

. Sine
00
2
(
y
) = 12
y
2
+ 6
y
+ (6
4
2
) has at most 1 positive zero, and
0
2
(
y
) = 4
y
3
+ 3
y
2
+ (6
4
2
)
y
(3
+ 9
)
<
0 at
y
= 0, we know that
0
2
(
y
) has at most one positive
zero. Thus
2
(
y
) has at most 2 positive zeros. This means
0
1
(
x
) has at most two p ositive zeros, so
0
(
x
)
has at most three (p ositive) zeros.
ase 3:
<
0
Notie that
0
(
x
)
<
0 for
x
2
[0
;
p
=
(3
) ℄ and
0
(
x
)
>
0 for
x
2
(
1
;
p
=
(3
) ℄. So we only
look for solutions
x
2
(
p
=
(3
)
;
1
) and
x
2
(
p
=
(3
)
;
0). Let
y
=
+ 3
x
2
, then there is a one
to one mapping b etween the
x
in the ab ove range and
y
2
(
;
1
). Let
1
(
x
) and
2
(
y
) have the same
expressions as in ase 2. We have that
2
(
y
) has at most four zeros sine it is a fourth order p olynomial.
Notie that
2
(
)
<
0
;
2
(
1
)
>
0, so
2
(
y
) has at most three zeros in (
;
1
). This means
0
1
(
x
) has
at most three zeros, hene
0
(
x
) has at most four zeros.
Figure 1 illustrates the result of prop osition 2 by depiting a unimo dal and a bimo dal pdf from the
univariate FGSN with
K
= 3. For
K
= 1, the p df is always unimodal as was already noted by Azzalini
(1985) for the univariate skew-normal distribution.
Next we investigate the exibility of the FGSN distribution in the bivariate ase. Its pdf for
K
= 3,
=
0
, and =
I
2
is given by:
2
2
(
x
1
; x
2
;
0
; I
2
)(
1
x
1
+
2
x
2
+
1
x
3
1
+
2
x
3
2
+
3
x
2
1
x
2
+
4
x
1
x
2
2
)
:
(8)
Figure 2 should b e here.
Figure 2 depits the ontours of four dierent pdfs (8) for various ombinations of values of the
skewness parameters
1
,
2
,
1
,
2
,
3
, and
4
. In partiular, for
1
=
2
=
3
=
4
= 0, the
pdf is exatly the bivariate skew-normal proposed by Azzalini & Dalla Valle (1996), and known to be
unimodal, see Figure 2(a). However, Figures 2(b)-(d) show that many dierent distributional shap es an
be obtained with the parameters
1
; : : : ;
4
, in partiular bimodal and trimo dal distributions. Additional
5
Citations
More filters
Journal Article•DOI•
Alpha-Skew Generalized t Distribution

[...]

Sukru Acitas1, Birdal Şenoğlu2, Olcay Arslan2•
Anadolu University1, Ankara University2
01 Jul 2015-Revista Colombiana de Estadistica
TL;DR: In this paper, the authors proposed an alpha-skew generalized t (ASGT) by using the generalized t (GT) distribution and a new skewing procedure, which is able to model both skew and bimodal data.
Abstract: The alpha-skew normal (ASN) distribution has been proposed recently in the literature by using standard normal distribution and a skewing approach. Although ASN distribution is able to model both skew and bimodal data, it is shortcoming when data has thinner or thicker tails than normal. Therefore, we propose an alpha-skew generalized t (ASGT) by using the generalized t (GT) distribution and a new skewing procedure. From this point of view, ASGT can be seen as an alternative skew version of GT distribution. However, ASGT differs from the previous skew versions of GT distribution since it is able to model bimodal data sest as well as it nests most commonly used density functions. In this paper, moments and maximum likelihood estimation of the parameters of ASGT distribution are given. Skewness and kurtosis measures are derived based on the first four noncentral moments. The cumulative distribution function (cdf) of ASGT distribution is also obtained. In the application part of the study, two real life problems taken from the literature are modeled by using ASGT distribution.

14 citations

Journal Article•
A Matrix Variate Skew Distribution

[...]

Deniz Akdemir, Arjun K. Gupta
10 Apr 2010-European Journal of Pure and Applied Mathematics
TL;DR: In this paper, a class of flexible matrix variate distribution models that can represent both skewed and symmetric distributions is studied, which can also account for dependence among individual observations, and the moment generating function is derived.
Abstract: Typical multivariate analysis assumes independence among the individual observations as well as elliptical symmetry of distributions. In many situations these assumptions may be too restrictive. This paper studies a class of flexible matrix variate distribution models that can represent both skewed and symmetric distributions which can also account for dependence among individual observations. We derive the moment generating function and study linear and quadratic forms of interest that help understand the properties of these models.

14 citations

Cites methods from "Flexible Class of Skew‐Symmetric Di..."

  • ...[8] Y.Y. Ma and M.G. Genton....

    [...]

  • ...[1]; if we take w(x) = αx + β x3, we obtain a matrix variate form of the skew symmetric family introduced by Ma and Genton [8]; or take w(x) = si gn(x)|x |α/2λ(2/α)1/2 to obtain a matrix variate form of the skew symmetric family introduced by DiCiccio and Monti [5]....

    [...]

  • ...[1]; if we take w(x) = αx + β x(3), we obtain a matrix variate form of the skew symmetric family introduced by Ma and Genton [8]; or take w(x) = si gn(x)|x |α/2λ(2/α)1/2 to obtain a matrix variate form of the skew symmetric family introduced by DiCiccio and Monti [5]....

    [...]

Journal Article•DOI•
Flexible Skew-Symmetric Shape Model for Shape Representation, Classification, and Sampling

[...]

Sajjad Baloch1, Hamid Krim1•
North Carolina State University1
01 Feb 2007-IEEE Transactions on Image Processing
TL;DR: A novel statistical method for shape modeling, which is sufficiently flexible to accommodate a departure from Gaussianity of the data and is fairly general to learn a "mean shape" (template), with a potential for classification and random generation of new realizations of a given shape.
Abstract: Skewness of shape data often arises in applications (eg, medical image analysis) and is usually overlooked in statistical shape models In such cases, a Gaussian assumption is unrealistic and a formulation of a general shape model which accounts for skewness is in order In this paper, we present a novel statistical method for shape modeling, which we refer to as the flexible skew-symmetric shape model (FSSM) The model is sufficiently flexible to accommodate a departure from Gaussianity of the data and is fairly general to learn a "mean shape" (template), with a potential for classification and random generation of new realizations of a given shape Robustness to skewness results from deriving the FSSM from an extended class of flexible skew-symmetric distributions In addition, we demonstrate that the model allows us to extract principal curves in a point cloud The idea is to view a shape as a realization of a spatial random process and to subsequently learn a shape distribution which captures the inherent variability of realizations, provided they remain, with high probability, within a certain neighborhood range around a mean Specifically, given shape realizations, FSSM is formulated as a joint bimodal distribution of angle and distance from the centroid of an aggregate of random points Mean shape is recovered from the modes of the distribution, while the maximum likelihood criterion is employed for classification

14 citations

Journal Article•DOI•
An overview on the progeny of the skew-normal family—A personal perspective

[...]

Adelchi Azzalini1•
University of Padua1
13 Oct 2021-Journal of Multivariate Analysis
TL;DR: The aim is to present a panoramic view of the skew-normal distribution theme, leaving out the fine details, with rather more emphasis on the evolution of the underlying ideas and on the breath of the overall developments.

13 citations

Journal Article•DOI•
Inference in flexible families of distributions with normal kernel

[...]

Gustavo H. M. A. Rocha1, Rosangela H. Loschi1, Reinaldo B. Arellano-Valle2•
Universidade Federal de Minas Gerais1, Pontifical Catholic University of Chile2
26 Sep 2013-Statistics
TL;DR: In this article, the inference problem for a flexible class of distributions with normal kernel known as skew-bimodal-normal family of distributions is addressed and conditions for the existence of the maximum-likelihood estimators (MLE) are provided.
Abstract: This paper addresses the inference problem for a flexible class of distributions with normal kernel known as skew-bimodal-normal family of distributions. We obtain posterior and predictive distributions assuming different prior specifications. We provide conditions for the existence of the maximum-likelihood estimators (MLE). An EM-type algorithm is built to compute them. As a by product, we obtain important results related to classical and Bayesian inferences for two special subclasses called bimodal-normal and skew-normal (SN) distribution families. We perform a Monte Carlo simulation study to analyse behaviour of the MLE and some Bayesian ones. Considering the frontier data previously studied in the literature, we use the skew-bimodal-normal (SBN) distribution for density estimation. For that data set, we conclude that the SBN model provides as good a fit as the one obtained using the location-scale SN model. Since the former is a more parsimonious model, such a result is shown to be more attractive.

11 citations

Cites methods from "Flexible Class of Skew‐Symmetric Di..."

  • ...Let x0 = (xT 0)T, xa = (xT(a/√vλ))T and m∗λ = mλ(0T(a/ √ vλ))T. Assuming normal or SN prior distributions for λ, the computation of the prior and the posterior expectations Eλ( n(λx)) and Eλ|x( m(λy)) (see Proposition 7) is straightforward from the following well-known lemma that can be found in Arellano-Valle and Genton [7], for instance....

    [...]

  • ...To cite a few, Ma and Genton [4], Wang et al....

    [...]

  • ...For other flexible classes of the SN distribution, see Ma and Genton [4]....

    [...]

  • ...An overview of some existent proposals for skewed distributions can be found in the book edited by Genton [10] and in Azzalini [2]....

    [...]

  • ...To cite a few, Ma and Genton [4], Wang et al. [5], Genton and Loperfido [6], Arellano-Valle and Genton [7], Arellano-Valle and Azzalini [8], and Azzalini and Genton [9]....

    [...]

References
More filters
Book•
Functional analysis

[...]

Walter Rudin
01 Jan 1973

14,545 citations

Journal Article•
A class of distributions which includes the normal ones

[...]

Adelchi Azzalini
01 Jan 1985-Scandinavian Journal of Statistics
TL;DR: In this paper, a nouvelle classe de fonctions de densite dependant du parametre de forme λ, telles que λ=0 corresponde a la densite normale standard.
Abstract: On introduit une nouvelle classe de fonctions de densite dependant du parametre de forme λ, telles que λ=0 corresponde a la densite normale standard

2,470 citations

"Flexible Class of Skew‐Symmetric Di..." refers background or methods in this paper

  • ...This representation has been used by Azzalini & Capitanio (2003) to define certain distributions by perturbation of symmetry....

    [...]

  • ...For K = 1, the pdf is always unimodal as was already noted by Azzalini (1985) for the univariate skew-normal distribution....

    [...]

  • ...The case K = 1 corresponds to Azzalini & Dalla Valle's (1996) bivariate skew-normal distribution, which cannot capture the bimodality....

    [...]

  • ...For K ¼ 1, the pdf is always unimodal as was already noted by Azzalini (1985) for the univariate skew-normal distribution....

    [...]

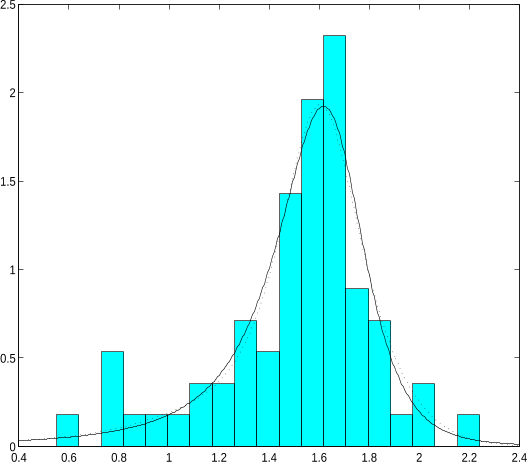
  • ...In particular, for ,il = ,B2 = /33 = & = 0, the pdf is exactly the bivariate skew-normal proposed by Azzalini & Dalla Valle (1996), and known to be unimodal (see Fig....

    [...]

Book•
Smoothing Methods in Statistics

[...]

Jeffrey S. Simonoff1•
University of Wisconsin-Madison1
06 Jun 1996
TL;DR: In this article, a nonparametric/parametric Compromise is used to improve the kernel density estimator, and the effect of simple Density Estimators is discussed.
Abstract: 1. Introduction.- 1.1 Smoothing Methods: a Nonparametric/Parametric Compromise.- 1.2 Uses of Smoothing Methods.- 1.3 Outline of the Chapters.- Background material.- Computational issues.- Exercises.- 2. Simple Univariate Density Estimation.- 2.1 The Histogram.- 2.2 The Frequency Polygon.- 2.3 Varying the Bin Width.- 2.4 The Effectiveness of Simple Density Estimators.- Background material.- Computational issues.- Exercises.- 3. Smoother Univariate Density Estimation.- 3.1 Kernel Density Estimation.- 3.2 Problems with Kernel Density Estimation.- 3.3 Adjustments and Improvements to Kernel Density Estimation.- 3.4 Local Likelihood Estimation.- 3.5 Roughness Penalty and Spline-Based Methods.- 3.6 Comparison of Univariate Density Estimators.- Background material.- Computational issues.- Exercises.- 4. Multivariate Density Estimation.- 4.1 Simple Density Estimation Methods.- 4.2 Kernel Density Estimation.- 4.3 Other Estimators.- 4.4 Dimension Reduction and Projection Pursuit.- 4.5 The State of Multivariate Density Estimation.- Background material.- Computational issues.- Exercises.- 5. Nonparametrie Regression.- 5.1 Scatter Plot Smoothing and Kernel Regression.- 5.2 Local Polynomial Regression.- 5.3 Bandwidth Selection.- 5.4 Locally Varying the Bandwidth.- 5.5 Outliers and Autocorrelation.- 5.6 Spline Smoothing.- 5.7 Multiple Predictors and Additive Models.- 5.8 Comparing Nonparametric Regression Methods.- Background material.- Computational issues.- Exercises.- 6. Smoothing Ordered Categorical Data.- 6.1 Smoothing and Ordered Categorical Data.- 6.2 Smoothing Sparse Multinomials.- 6.3 Smoothing Sparse Contingency Tables.- 6.4 Categorical Data, Regression, and Density Estimation.- Background material.- Computational issues.- Exercises.- 7. Further Applications of Smoothing.- 7.1 Discriminant Analysis.- 7.2 Goodness-of-Fit Tests.- 7.3 Smoothing-Based Parametric Estimation.- 7.4 The Smoothed Bootstrap.- Background material.- Computational issues.- Exercises.- Appendices.- A. Descriptions of the Data Sets.- B. More on Computational Issues.- References.- Author Index.

1,719 citations

Journal Article•DOI•
The multivariate skew-normal distribution

[...]

Adelchi Azzalini, A. Dalla Valle
01 Dec 1996-Biometrika
TL;DR: In this article, a multivariate parametric family such that the marginal densities are scalar skew-normal is introduced, and its properties are studied with special emphasis on the bivariate case.
Abstract: SUMMARY The paper extends earlier work on the so-called skew-normal distribution, a family of distributions including the normal, but with an extra parameter to regulate skewness. The present work introduces a multivariate parametric family such that the marginal densities are scalar skew-normal, and studies its properties, with special emphasis on the bivariate case.

1,478 citations

Journal Article•DOI•
Distributions generated by perturbation of symmetry with emphasis on a multivariate skew t‐distribution

[...]

Adelchi Azzalini1, Antonella Capitanio1•
University of Padua1
01 May 2003-Journal of The Royal Statistical Society Series B-statistical Methodology
TL;DR: In this paper, a fairly general procedure is studied to perturb a multivariate density satisfying a weak form of multivariate symmetry, and to generate a whole set of non-symmetric densities.
Abstract: Summary. A fairly general procedure is studied to perturb a multivariate density satisfying a weak form of multivariate symmetry, and to generate a whole set of non-symmetric densities. The approach is sufficiently general to encompass some recent proposals in the literature, variously related to the skew normal distribution. The special case of skew elliptical densities is examined in detail, establishing connections with existing similar work. The final part of the paper specializes further to a form of multivariate skew t-density. Likelihood inference for this distribution is examined, and it is illustrated with numerical examples.

1,215 citations

"Flexible Class of Skew‐Symmetric Di..." refers background in this paper

  • ...Finally, note that the stochastic representation of FSSdistributions follows from the stochastic representation of SS distributions described byWang et al. (2004), see also Azzalini & Capitanio (2003)....

    [...]

  • ...Similarly, multivariate distributions such as skew-t (Branco & Dey, 2001; Azzalini & Capitanio, 2003; Jones & Faddy, 2003; Sahu et al., 2003), skew-Cauchy (Arnold & Beaver, 2000) and other skewelliptical ones (Azzalini & Capitanio, 1999; Branco & Dey, 2001; Sahu et al., 2003) can be represented by…...

    [...]

  • ...Jones & Faddy (2003) and Azzalini & Capitanio (2003) fit two forms of skew-t distributions to these data....

    [...]

  • ...If each term has an odd order (all ks are odd), then the polynomial is called an odd polynomial, whereas if each term has an even order (all ks are even), it is called an even polynomial....

    [...]

Related Papers (5)
A class of distributions which includes the normal ones

[...]

01 Jan 1985-Scandinavian Journal of Statistics
Adelchi Azzalini
Distributions generated by perturbation of symmetry with emphasis on a multivariate skew t‐distribution

[...]

01 May 2003-Journal of The Royal Statistical Society Series B-statistical Methodology
Adelchi Azzalini, Antonella Capitanio
The multivariate skew-normal distribution

[...]

01 Dec 1996-Biometrika
Adelchi Azzalini, A. Dalla Valle
Skew-Elliptical Distributions and Their Applications : A Journey Beyond Normality

[...]

27 Jul 2004
Marc G. Genton
A General Class of Multivariate Skew-Elliptical Distributions

[...]

01 Oct 2001-Journal of Multivariate Analysis
Márcia D. Branco, Dipak K. Dey