scispace - formally typeset
Search or ask a question
Journal Article•DOI•

Flexible Class of Skew‐Symmetric Distributions

Yanyuan Ma1, Marc G. Genton1•
North Carolina State University1
01 Sep 2004-Scandinavian Journal of Statistics (Blackwell)-Vol. 31, Iss: 3, pp 459-468
TL;DR: In this paper, a flexible class of skew-symmetric distributions for which the probab- ility density function has the form of a product of a symmetric density and a skewing function is proposed.
Abstract: We propose a flexible class of skew-symmetric distributions for which the probab- ility density function has the form of a product of a symmetric density and a skewing function. By constructing an enumerable dense subset of skewing functions on a compact set, we are able to consider a family of distributions, which can capture skewness, heavy tails and multimodality systematically. We present three illustrative examples for the fibreglass data, the simulated data from a mixture of two normal distributions and the Swiss bills dlata.
Figures (4)

Content maybe subject to copyright    Report

A Flexible Class of Skew-Symmetri Distributions
(running head: exible skew-symmetri distributions)
YANYUAN MA
North Carolina State University
MARC G. GENTON
North Carolina State University
ABSTRACT. We prop ose a exible lass of skew-symmetri distributions for whih the
probability density funtion has the form of a pro dut of a symmetri density and a skewing
funtion. By onstruting an enumerable dense subset of skewing funtions on a ompat
set, we are able to onsider a family of distributions whih an apture skewness, heavy
tails, and multimo dality systematially. We present three illustrative examples for the
b er-glass data, simulated data from a mixture of two normal distributions, and Swiss
bills data.
Key Words:
dense subset; generalized skew-elliptial; multimodality; skewness; skew-normal.
1 Intro dution
A popular approah to ahieve departures from normality onsists of modifying the probability density
funtion (p df ) of a random vetor in a multipliative fashion. Wang, Boyer, & Genton (2004) showed
that any
p
-dimensional multivariate pdf
g
(
x
) admits, for any xed loation parameter
2
R
p
, a unique
skew-symmetri (SS) representation:
g
(
x
) = 2
f
(
x
)
(
x
)
;
(1)
where
f
:
R
p
!
R
+
is a symmetri p df and
:
R
p
!
[0
;
1℄ is a skewing funtion satisfying
(
x
) =
1
(
x
). Vie-versa, any funtion
g
of the type dened by (1) is a valid pdf. By symmetri, we mean
f
(
x
) =
f
(
x
) and we will use \symmetri pdf " and the prop erty
f
(
x
) =
f
(
x
) interhangeably in
the sequel. Throughout this pap er, we restrit our interest on funtions
f
2
C
0
(
R
p
) and ontinuous
skewing funtions
(
x
), where
C
0
(
R
p
) denotes ontinuous funtions on
R
p
with the prop erty
f
(
x
)
!
0
when
k
x
k
2
! 1
, and
k k
2
denotes the
L
2
norm. Genton & Lop erdo (2002) onsidered the subfamily
of generalized skew-elliptial (GSE) distributions for whih the p df
f
in (1) is elliptially ontoured
rather than only symmetri. Many denitions of skewed distributions found in the literature an be
written in the form of a skew-symmetri distribution (1). For instane, Azzalini & Dalla Valle's (1996)
multivariate skew-normal distribution orresp onds to
f
(
x
) =
p
(
x
;
0
;
) and
(
x
) = (
T
x
), where
p
(
x
;
;
) is the
p
-dimensional multivariate normal pdf with mean vetor
and orrelation matrix ,
1
is the standard normal umulative distribution funtion (df ), and
is a shap e parameter ontrolling
skewness. Similarly, multivariate distributions suh as skew-
t
(Brano & Dey, 2001; Azzalini & Capitanio,
2003; Jones & Faddy, 2003; Sahu, Brano, & Dey, 2003), skew-Cauhy (Arnold & Beaver, 2000) and
other skew-elliptial ones (Azzalini & Capitanio, 1999; Brano & Dey, 2001; Sahu
et al.
, 2003) an be
represented by the skew-symmetri distribution (1) with appropriate hoies of
f
and
.
In this artile, we prop ose a exible lass of distributions (1) by onstruting an enumerable dense
subset of the skewing funtions
on a ompat set. The result is a family of distributions whih
an apture skewness, heavy tails, and multimodality systematially. The onstrution of the subset is
through p olynomials, whih has a similar avor as the seminonparametri (SNP) representation prop osed
by Gallant & Nyhka (1987). The latter is dened as the pro dut of the standard normal p df and the
square of a polynomial. The SNP distribution requires the oeÆients in the polynomial to b e onstrained
in order to yield a valid density. It also relies on rejetion sampling shemes to simulate random samples.
These diÆulties do not o ur with our onstrution.
The ontent of the pap er is organized as follows. In Setion 2, we desribe a subset of skewing
funtions based on o dd p olynomials and prove that it results in a dense subset of the skew-symmetri
distributions. In partiular, we dene exible skew-normal and skew-
t
distributions that an have more
than one mode. This is an essential property for some situations and provides an alternative to modeling
with mixtures of distributions. The exibility and p ossible multimodality of the new lass of distributions
is illustrated in Setion 3. We present three illustrative examples in Setion 4, and a disussion in Setion
5.
2 A dense subset of skew-symmetri distributions
In this setion, we onstrut a dense subset of skew-symmetri distributions through approximating the
skewing funtion
on a ompat set. Any ontinuous skewing funtion
an be written as:
(
x
) =
H
(
w
(
x
))
;
(2)
where
H
:
R
!
[0
;
1℄ is the df of a ontinuous random variable symmetri around 0, and
w
:
R
p
!
R
is an o dd ontinuous funtion, that is
w
(
x
) =
w
(
x
). In fat, for a hosen
H
suh that
H
1
exists,
w
(
x
) =
H
1
(
(
x
)) is a ontinuous odd funtion. This representation has been used by Azzalini &
Capitanio (2003) to dene ertain distributions by p erturbation of symmetry. Note however that the
representation (2) is not unique due to the many possible hoies of
H
.
Let
P
K
(
x
) b e an o dd p olynomial of order
K
. A p olynomial of order
K
in
R
p
is dened as a linear
ombination of terms of the form
Q
p
i
=1
x
r
i
i
, where
k
=
P
p
i
=1
r
i
K
. If eah term has an odd order (all
k
's are o dd), then the polynomial is alled an odd p olynomial, whereas if eah term has an even order
(all
k
's are even), it is alled an even polynomial. We dene exible skew-symmetri (FSS) distributions
2
by restriting (1) to:
2
f
(
x
)
K
(
x
)
;
(3)
where
K
(
x
) =
H
(
P
K
(
x
)) and
H
is any df of a ontinuous random variable symmetri around 0. Note
that there are no onstraints on the oeÆients of the p olynomial
P
K
in order to make (3) a valid
pdf. In partiular, (3) denes exible generalized skew-elliptial (FGSE) distributions when the pdf
f
is
elliptially ontoured. For instane, exible generalized skew-normal (FGSN) distributions are dened
by:
2
p
(
x
;
;
)(
P
K
(
A
(
x
)))
;
(4)
and exible generalized skew-
t
(FGST) distributions are dened by:
2
t
p
(
x
;
;
;
)
T
(
P
K
(
A
(
x
));
)
;
(5)
where we use the Choleski deomposition
1
=
A
T
A
,
t
p
denotes a
p
-dimensional multivariate
t
pdf,
and
T
denotes a univariate
t
df, both with degrees of freedom
. Note that we ould use , or any
other symmetri df, instead of
T
for the skewing funtion in (5). In pratie, a popular hoie for the
df
H
would b e or the univariate df orresponding to the symmetri p df
f
. Eetively, the following
proposition shows that FSS distributions an approximate skew-symmetri distributions arbitrarily well.
Prop osition 1
Let the lass of exible skew-symmetri (FSS) distributions onsist of distributions with
pdf given in (3) and the lass of skew-symmetri (SS) distributions of distributions with pdf given in (1),
where
f
2
C
0
(
R
p
)
in both lasses and
is ontinuous. Then the lass of FSS distributions is dense in
the lass of SS distributions under the
L
1
norm.
Pro of
: An arbitrary distribution in the SS lass an be written as 2
f
(
x
)
H
(
w
(
x
)), where
f
and
H
are ontinuous,
H
1
exists, and
w
is a ontinuous o dd funtion. Beause
f
2
C
0
(
R
p
), for any arbitrary
>
0, we an nd a ompat set
D
whih is symmetri around
(if
x
2
D
then
x
2
D
), suh that
for any
x
=
2
D
,
f
(
x
)
< =
4. Thus, for any
x
=
2
D
,
j
2
f
(
x
)
(
x
)
2
f
(
x
)
H
(
P
((
x
))
j
<
for any odd p olynomial
P
.
Sine
f
is ontinuous,
f
is bounded on
D
. We denote the bound by
C
, i.e.
f
(
x
)
C
for any
x
2
D
. We use
D
1
to denote the image spae of
w
, i.e.
D
1
=
f
w
(
x
)
j
x
2
D
g
. Beause of the
ontinuity of
w
, whih is a result of the ontinuity of b oth
H
and
,
D
1
is also ompat. The ontinuous
funtion
H
is uniformly ontinuous on the ompat set
D
1
. Hene there exists
>
0 suh that for
any
y
1
,
y
2
2
D
1
and
j
y
1
y
2
j
<
, we get
j
H
(
y
1
)
H
(
y
2
)
j
< =
(2
C
). From the Stone-Weierstrass
theorem (see e.g. Rudin, 1973, p. 115), there exists a polynomial
P
suh that
j
w
(
x
)
P
(
x
)
j
<
for any
x
2
D
. We deomp ose
P
into an even term
P
e
and an odd term
P
o
, i.e.
P
=
P
e
+
P
o
.
Then
j
w
(
x
)
P
e
(
x
)
P
o
(
x
)
j
<
and
j
w
(
x
)
P
e
(
x
)
P
o
(
x
)
j
<
. Beause
w
and
P
o
are odd, and
P
e
is even, we get
j
w
(
x
)
P
e
(
x
) +
P
o
(
x
)
j
<
. Notie that
2
j
w
(
x
)
P
o
(
x
)
j j
w
(
x
)
P
e
(
x
)
P
o
(
x
)
j
+
j
w
(
x
)
P
e
(
x
) +
P
o
(
x
)
j
<
2
,
3
so
j
w
(
x
)
P
o
(
x
)
j
<
. Combining these results, we know that for an arbitrary member
2
f
(
x
)
H
(
w
(
x
)) in SS and an arbitrary
>
0, we an nd a member 2
f
(
x
)
H
(
P
o
(
x
)) in
FSS suh that
j
2
f
(
x
)
H
(
w
(
x
))
2
f
(
x
)
H
(
P
o
(
x
))
j
<
for any
x
2
D
.
Hene FSS is dense in SS with resp et to the
L
1
norm.
Remark 1
The requirement
f
2
C
0
(
R
p
)
in proposition 1 an be relaxed to al low that
f
has a nite
number,
m
say, of poles. In this ase, FSS is dense in SS with respet to almost uniform onvergene
(uniform in a set whose omplement is of measure arbitrarily smal l). Indeed, let
R
p
(
r
)
denote
R
p
minus
the union of
m
open bal ls of radius
r
entered at the
m
poles. Then FSS is dense in SS on
R
p
(
r
)
under
the
L
1
norm. Letting
r
!
0
, the result fol lows.
Proposition 1 shows in partiular that the lass of generalized skew-elliptial, skew
t
, and skew-
normal distributions an b e approximated arbitrarily well by their exible versions.
3 Flexibility and multimodality
In Figure 1, we illustrate the shap e exibility of the FGSN distribution in the univariate ase. Its pdf
for
K
= 3 is dened by:
2
1
(
x
;
;
2
)(
(
x
)
=
+
(
x
)
3
=
3
)
:
(6)
Figure 1 should b e here.
Figure 1(a) depits the p df of the FGSN model for
= 0,
2
= 1,
= 4, and
= 0, i.e. it redues
to Azzalini's (1985) univariate skew-normal distribution. However, when
6
= 0, the p df (6) an exhibit
bimodality as shown in Figure 1(b) with
= 1, and
=
1. In general, as the degree
K
of the o dd
polynomial in the skewing funtion beomes large, the number of mo des allowed in the p df inreases,
thus induing a greater exibility in the available shapes. Unfortunately, the number of modes depends
on the degree
K
of the o dd p olynomial, on the symmetri pdf
f
, and on the df
H
of the skewing
funtion
K
in a omplex fashion. Indeed, even for the univariate situation given by
p
= 1, the mo des
are determined by zeros of the rst derivative of the FSS distribution (3) given by:
2
f
0
(
x
)
H
(
P
K
(
x
)) + 2
f
(
x
)
H
0
(
P
K
(
x
))
P
0
K
(
x
)
;
(7)
for whih the number of zeros annot b e easily omputed. Even with restritions to some sp ei
f
and
H
funtions, a general statement on the relation between the number of mo des and the order of the
polynomial seems not available. However, in the univariate ase, if we onsider a normal pdf
f
=
1
and
a standard normal df
H
= with an o dd p olynomial of order
K
= 3, we have the following proposition.
Prop osition 2
The lass of exible generalized skew-normal (FGSN) distributions with pdf
2
1
(
x
;
;
2
)(
(
x
)
=
+
(
x
)
3
=
3
)
has at most 2 modes.
4
Pro of
: Without loss of generality, we an set
= 0,
= 1, assume
>
0, and only need to prove that
(
x
) = 2
(
x
)(
x
+
x
3
) has at most two modes. We prove this by ontradition. If
(
x
) has more
than two mo des, then
0
(
x
) has at least ve zeros. In the following pro of, we show that this annot b e
the ase. We have
0
(
x
) = 2
(
x
)((
+ 3
x
2
)
(
x
+
x
3
)
x
(
x
+
x
3
)) and need to onsider three
ases:
ase 1:
= 0
We write
0
(
x
) = 2
x
(
x
)
(
x
), where
(
x
) = 3
x
(
x
3
)
(
x
3
). We an verify that
0
(
x
) =
3
(
x
3
)
1
(
y
) where
y
=
x
2
and
1
(
y
) = 1
y
3
2
y
3
. Sine
1
(
y
) is a dereasing funtion on
y
0,
0
(
x
) has at most two zeros. Thus,
(
x
) has at most three zeros, hene
0
(
x
) has at most four
zeros.
ase 2:
>
0
Notie that
0
(
x
)
>
0 for
x
0. For
1
(
x
) =
0
(
x
)
=
(2
x
(
x
)) =
(
x
+
x
3
)(
+ 3
x
2
)
=x
(
x
+
x
3
),
we get
0
1
(
x
) =
(
x
+
x
3
)
=
(
9
x
2
)
2
(
y
), where
y
=
+ 3
x
2
>
0 and
2
(
y
) =
y
4
+
y
3
+ (3
2
2
)
y
2
(3
+ 9
)
y
+ 18

. Sine
00
2
(
y
) = 12
y
2
+ 6
y
+ (6
4
2
) has at most 1 positive zero, and
0
2
(
y
) = 4
y
3
+ 3
y
2
+ (6
4
2
)
y
(3
+ 9
)
<
0 at
y
= 0, we know that
0
2
(
y
) has at most one positive
zero. Thus
2
(
y
) has at most 2 positive zeros. This means
0
1
(
x
) has at most two p ositive zeros, so
0
(
x
)
has at most three (p ositive) zeros.
ase 3:
<
0
Notie that
0
(
x
)
<
0 for
x
2
[0
;
p
=
(3
) ℄ and
0
(
x
)
>
0 for
x
2
(
1
;
p
=
(3
) ℄. So we only
look for solutions
x
2
(
p
=
(3
)
;
1
) and
x
2
(
p
=
(3
)
;
0). Let
y
=
+ 3
x
2
, then there is a one
to one mapping b etween the
x
in the ab ove range and
y
2
(
;
1
). Let
1
(
x
) and
2
(
y
) have the same
expressions as in ase 2. We have that
2
(
y
) has at most four zeros sine it is a fourth order p olynomial.
Notie that
2
(
)
<
0
;
2
(
1
)
>
0, so
2
(
y
) has at most three zeros in (
;
1
). This means
0
1
(
x
) has
at most three zeros, hene
0
(
x
) has at most four zeros.
Figure 1 illustrates the result of prop osition 2 by depiting a unimo dal and a bimo dal pdf from the
univariate FGSN with
K
= 3. For
K
= 1, the p df is always unimodal as was already noted by Azzalini
(1985) for the univariate skew-normal distribution.
Next we investigate the exibility of the FGSN distribution in the bivariate ase. Its pdf for
K
= 3,
=
0
, and =
I
2
is given by:
2
2
(
x
1
; x
2
;
0
; I
2
)(
1
x
1
+
2
x
2
+
1
x
3
1
+
2
x
3
2
+
3
x
2
1
x
2
+
4
x
1
x
2
2
)
:
(8)
Figure 2 should b e here.
Figure 2 depits the ontours of four dierent pdfs (8) for various ombinations of values of the
skewness parameters
1
,
2
,
1
,
2
,
3
, and
4
. In partiular, for
1
=
2
=
3
=
4
= 0, the
pdf is exatly the bivariate skew-normal proposed by Azzalini & Dalla Valle (1996), and known to be
unimodal, see Figure 2(a). However, Figures 2(b)-(d) show that many dierent distributional shap es an
be obtained with the parameters
1
; : : : ;
4
, in partiular bimodal and trimo dal distributions. Additional
5
Citations
More filters
Journal Article•DOI•
Bayesian approach to errors-in-variables in count data regression models with departures from normality and overdispersion

[...]

Nur Aainaa Rozliman1, Adriana Irawati Nur Ibrahim1, Rossita Muhamad Yunus1•
University of Malaya1
22 Jan 2018-Journal of Statistical Computation and Simulation
TL;DR: In this paper, the quality of count data is often compromised due to errors-in-variables (EIVs) in most practical applications, and they apply Bayesian approach to reduce bias in estimating the paramete...
Abstract: In most practical applications, the quality of count data is often compromised due to errors-in-variables (EIVs). In this paper, we apply Bayesian approach to reduce bias in estimating the paramete...

1 citations

Journal Article•DOI•
Likelihood Inference of Nonlinear Models Based on a Class of Flexible Skewed Distributions

[...]

Xuedong Chen, Qianying Zeng, Qiankun Song
03 Dec 2014-Abstract and Applied Analysis
TL;DR: In this paper, a modified Newton-Raphson iterative algorithm is presented based on profile likelihood for nonlinear regression models with FSTN distribution, and, then, the confidence interval and hypothesis test are also developed.
Abstract: This paper deals with the issue of the likelihood inference for nonlinear models with a flexible skew-t-normal (FSTN) distribution, which is proposed within a general framework of flexible skew-symmetric (FSS) distributions by combining with skew-t-normal (STN) distribution. In comparison with the common skewed distributions such as skew normal (SN), and skew-t (ST) as well as scale mixtures of skew normal (SMSN), the FSTN distribution can accommodate more flexibility and robustness in the presence of skewed, heavy-tailed, especially multimodal outcomes. However, for this distribution, a usual approach of maximum likelihood estimates based on EM algorithm becomes unavailable and an alternative way is to return to the original Newton-Raphson type method. In order to improve the estimation as well as the way for confidence estimation and hypothesis test for the parameters of interest, a modified Newton-Raphson iterative algorithm is presented in this paper, based on profile likelihood for nonlinear regression models with FSTN distribution, and, then, the confidence interval and hypothesis test are also developed. Furthermore, a real example and simulation are conducted to demonstrate the usefulness and the superiority of our approach.

1 citations

Cites background from "Flexible Class of Skew‐Symmetric Di..."

  • ...Since then, several authors have tried to extend these results to more general forms of skew-symmetric distributions, of which here we would like to mention [9], in this paper; they proposed a general framework of distributions which is called flexible skewsymmetric (FSS) distribution....

    [...]

  • ...In this paper, with the adoption of a sufficiently flexible class of distributions, we consider one of these extensions, referred to as the family of flexible skew-symmetric (FSS) distributions which is introduced by [9] with the following density function of type: f (y; μ, ω,α) = 2ω −1 f 0 (z) G {P K (z)} , (1) where f...

    [...]

Efficient Semiparametric Estimators for Nonlinear Regressions and Models under Sample Selection Bias

[...]

Mi Jeong Kim
19 Oct 2012
TL;DR: Kim et al. as mentioned in this paper study the consistency, robustness and efficiency of parameter estimation in different but related models via semiparametric approach and propose consistent estimators for the center of the symmetric population.
Abstract: Efficient Semiparametric Estimators for Nonlinear Regressions and Models Under Sample Selection Bias. (August 2012) Mi Jeong Kim, B.S., Ewha University; M.S., Ewha University Chair of Advisory Committee: Dr. Yanyuan Ma We study the consistency, robustness and efficiency of parameter estimation in different but related models via semiparametric approach. First, we revisit the secondorder least squares estimator proposed in Wang and Leblanc (2008) and show that the estimator reaches the semiparametric efficiency. We further extend the method to the heteroscedastic error models and propose a semiparametric efficient estimator in this more general setting. Second, we study a class of semiparametric skewed distributions arising when the sample selection process causes sampling bias for the observations. We begin by assuming the anti-symmetric property to the skewing function. Taking into account the symmetric nature of the population distribution, we propose consistent estimators for the center of the symmetric population. These estimators are robust to model mis-specification and reach the minimum possible estimation variance. Next, we extend the model to permit a more flexible skewing structure. Without assuming a particular form of the skewing function, we propose both consistent and efficient estimators for the center of the symmetric population using a semiparametric method. We also analyze the asymptotic properties and derive the corresponding inference procedures. Numerical results are provided to support the results and illustrate the finite sample performance of the proposed estimators.

1 citations

Cites background from "Flexible Class of Skew‐Symmetric Di..."

  • ...For example, when w satisfies an anti-symmetric property, w(x;β,α) + w(x;β,α) = 1 for all x ∈ R, Copas and Li (1997), Arnold and Beaver (2002), Azzalini and Capitanio (2003), Ma and Genton (2004), Wang et al. (2004) and many others have described the types of selection mechanisms that lead to (1.1)....

    [...]

Book Chapter•DOI•
Empirical Likelihood-Based Method for LME Models

[...]

Haiyan Su1•
Montclair State University1
01 Jan 2014
TL;DR: Su et al. as mentioned in this paper developed an empirical likelihood-based method to get inference for population level parameter of interest in linear mixed-effects models when normality assumption is violated, which is a nonparametric method of inference based on a data-driven likelihood ratio function.
Abstract: Longitudinal data are often encountered in biomedical, epidemiological, social science and business studies. Repeated measurements are made on subjects over time and responses within a subject are usually correlated. The interest of longitudinal study is usually the growth curve over time. Linear mixed-effects models (LME) are widely used for longitudinal data because it allows both the population level fixed effects and individual level random effects to appear linearly in the model linearly in the model (Pinheiro & Bates, 2000). In modeling the fixed effects and random effects coefficients, the normality assumption of the random error terms and the random effect terms are required. Violation of this assumption may yield invalid statistical inference. Since the normality assumption is too restrictive as pointed out by Zhang and Davidian (2001, broader classes of distributions for the mixed models have been proposed by Verbeke and Lesaffre (1997), Zhang and Davidian (2001), Chen et al., (2002) among others. Ma and Genton (2004) relaxed the normality assumption by using semiparametric generalized skew-ellipitical distributions. Zhou and He (2008) replaced the normal distribution with skew-t distributions. Lachos et al., (2009) proposed a Bayesian approach with asymmetric heavy tailed distribution. The generalized estimation equation (GEE) (Liang & Zeger, 1986) approach relaxed this assumption by focusing on population-level effects using the quasi-likelihood method. GEE is a very popular approach researcher use when normality assumption is violated for continuous responses and it is supported by most available software such as SAS and R . In this paper, we develop an empirical likelihood-based method to get inference for population level parameter of interest in linear mixed-effects models when normality assumption is violated. Empirical likelihood was introduced by Owen (1988, 1990). It amounts to computing the parametric likelihood of a general multinomial distribution which has its atoms at all observed data points. Empirical likelihood provides a good alternative among the nonparametric methods that can be used to make statistical inference when the normality assumption is violated. The advantage of empirical likelihood compared to the bootstrap method and the jackknife method arises because it is a nonparametric method of inference based on a data-driven likelihood ratio function. A thorough summary of the advantages of empirical likelihood over its competitors is given in Hall and La Scala (1990). In this study, we suggest doing a projection to erase nuisance parameters for dimension reduction and then using the profile empirical likelihood principle. We then apply the Bartlett correction method to obtain the adjusted confidence interval. The paper is organized as follows: We give the main results including the model formulation, the Bartlett correction procedures and proofs of the theoretical results in the “Main Focus” section. Then follows results from simulation studies by comparing the proposed method with normal approximation method and the GEE method and a real application study. We then give the conclusion of the paper and the future trends. Haiyan Su Montclair State University, USA

1 citations

Cites methods from "Flexible Class of Skew‐Symmetric Di..."

  • ...Ma and Genton (2004) relaxed the normality assumption by using semiparametric generalized skew-ellipitical distributions....

    [...]

Journal Article•DOI•
Skewed and Flexible Skewed Distributions: A Modern Look at the Distribution of BMI

[...]

Thao Tran, Cara Wiskow, Mohammad Aziz
30 Jun 2017
TL;DR: In this paper, the authors used maximum likelihood estimation method to find distributions that best model body mass index (BMI) data and compared them to more conventional distributions, such as skew-normal and skew-t distributions, using AIC and BIC and Kolmogorov-Smirnov (K-S) goodness-of-fit test.
Abstract: ABSTRACT The purpose of this study is to find distributions that best model body mass index (BMI) data. BMI has become a standard health indicator and numerous studies have been done to examine the distribution of BMI. Due to the skew and bimodal nature, we focus on modeling BMI with flexible skewed distributions. The distributions are fitted to University of Wisconsin–Eau Claire (UWEC) BMI data and to data obtained from National Health and Nutrition Survey (NHANES). The model parameters are obtained using maximum likelihood estimation method. We compare flexible models to more conventional distributions, such as skew-normal and skew-t distributions, using AIC and BIC and Kolmogorov-Smirnov (K-S) goodness-of-fit test. Our results indicate that the skew-t and Alpha-Skew-Laplace distributions are reasonably competitive when describing unimodal BMI data whereas Alpha-Skew-Laplace, finite mixture of scale mixture of skew-normal and skew-t distributions are better alternatives to both unimodal and bimodal conventional distributions. The results we obtained are useful because we believe the models discussed in our study will offer a framework for testing features such as bimodality, asymmetry, and robustness of the BMI data, thus providing a more detailed and accurate understanding of the distribution of BMI.

1 citations

References
More filters
Book•
Functional analysis

[...]

Walter Rudin
01 Jan 1973

14,545 citations

Journal Article•
A class of distributions which includes the normal ones

[...]

Adelchi Azzalini
01 Jan 1985-Scandinavian Journal of Statistics
TL;DR: In this paper, a nouvelle classe de fonctions de densite dependant du parametre de forme λ, telles que λ=0 corresponde a la densite normale standard.
Abstract: On introduit une nouvelle classe de fonctions de densite dependant du parametre de forme λ, telles que λ=0 corresponde a la densite normale standard

2,470 citations

"Flexible Class of Skew‐Symmetric Di..." refers background or methods in this paper

  • ...This representation has been used by Azzalini & Capitanio (2003) to define certain distributions by perturbation of symmetry....

    [...]

  • ...For K = 1, the pdf is always unimodal as was already noted by Azzalini (1985) for the univariate skew-normal distribution....

    [...]

  • ...The case K = 1 corresponds to Azzalini & Dalla Valle's (1996) bivariate skew-normal distribution, which cannot capture the bimodality....

    [...]

  • ...For K ¼ 1, the pdf is always unimodal as was already noted by Azzalini (1985) for the univariate skew-normal distribution....

    [...]

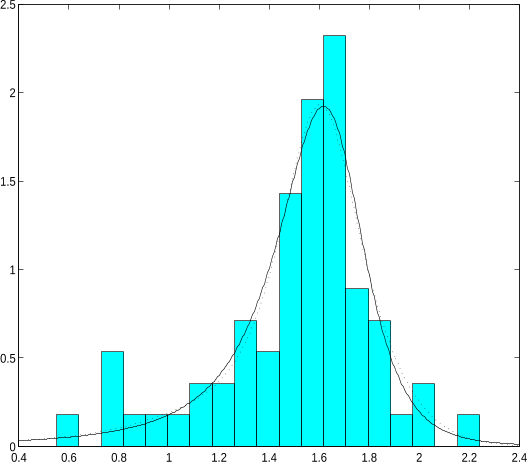
  • ...In particular, for ,il = ,B2 = /33 = & = 0, the pdf is exactly the bivariate skew-normal proposed by Azzalini & Dalla Valle (1996), and known to be unimodal (see Fig....

    [...]

Book•
Smoothing Methods in Statistics

[...]

Jeffrey S. Simonoff1•
University of Wisconsin-Madison1
06 Jun 1996
TL;DR: In this article, a nonparametric/parametric Compromise is used to improve the kernel density estimator, and the effect of simple Density Estimators is discussed.
Abstract: 1. Introduction.- 1.1 Smoothing Methods: a Nonparametric/Parametric Compromise.- 1.2 Uses of Smoothing Methods.- 1.3 Outline of the Chapters.- Background material.- Computational issues.- Exercises.- 2. Simple Univariate Density Estimation.- 2.1 The Histogram.- 2.2 The Frequency Polygon.- 2.3 Varying the Bin Width.- 2.4 The Effectiveness of Simple Density Estimators.- Background material.- Computational issues.- Exercises.- 3. Smoother Univariate Density Estimation.- 3.1 Kernel Density Estimation.- 3.2 Problems with Kernel Density Estimation.- 3.3 Adjustments and Improvements to Kernel Density Estimation.- 3.4 Local Likelihood Estimation.- 3.5 Roughness Penalty and Spline-Based Methods.- 3.6 Comparison of Univariate Density Estimators.- Background material.- Computational issues.- Exercises.- 4. Multivariate Density Estimation.- 4.1 Simple Density Estimation Methods.- 4.2 Kernel Density Estimation.- 4.3 Other Estimators.- 4.4 Dimension Reduction and Projection Pursuit.- 4.5 The State of Multivariate Density Estimation.- Background material.- Computational issues.- Exercises.- 5. Nonparametrie Regression.- 5.1 Scatter Plot Smoothing and Kernel Regression.- 5.2 Local Polynomial Regression.- 5.3 Bandwidth Selection.- 5.4 Locally Varying the Bandwidth.- 5.5 Outliers and Autocorrelation.- 5.6 Spline Smoothing.- 5.7 Multiple Predictors and Additive Models.- 5.8 Comparing Nonparametric Regression Methods.- Background material.- Computational issues.- Exercises.- 6. Smoothing Ordered Categorical Data.- 6.1 Smoothing and Ordered Categorical Data.- 6.2 Smoothing Sparse Multinomials.- 6.3 Smoothing Sparse Contingency Tables.- 6.4 Categorical Data, Regression, and Density Estimation.- Background material.- Computational issues.- Exercises.- 7. Further Applications of Smoothing.- 7.1 Discriminant Analysis.- 7.2 Goodness-of-Fit Tests.- 7.3 Smoothing-Based Parametric Estimation.- 7.4 The Smoothed Bootstrap.- Background material.- Computational issues.- Exercises.- Appendices.- A. Descriptions of the Data Sets.- B. More on Computational Issues.- References.- Author Index.

1,719 citations

Journal Article•DOI•
The multivariate skew-normal distribution

[...]

Adelchi Azzalini, A. Dalla Valle
01 Dec 1996-Biometrika
TL;DR: In this article, a multivariate parametric family such that the marginal densities are scalar skew-normal is introduced, and its properties are studied with special emphasis on the bivariate case.
Abstract: SUMMARY The paper extends earlier work on the so-called skew-normal distribution, a family of distributions including the normal, but with an extra parameter to regulate skewness. The present work introduces a multivariate parametric family such that the marginal densities are scalar skew-normal, and studies its properties, with special emphasis on the bivariate case.

1,478 citations

Journal Article•DOI•
Distributions generated by perturbation of symmetry with emphasis on a multivariate skew t‐distribution

[...]

Adelchi Azzalini1, Antonella Capitanio1•
University of Padua1
01 May 2003-Journal of The Royal Statistical Society Series B-statistical Methodology
TL;DR: In this paper, a fairly general procedure is studied to perturb a multivariate density satisfying a weak form of multivariate symmetry, and to generate a whole set of non-symmetric densities.
Abstract: Summary. A fairly general procedure is studied to perturb a multivariate density satisfying a weak form of multivariate symmetry, and to generate a whole set of non-symmetric densities. The approach is sufficiently general to encompass some recent proposals in the literature, variously related to the skew normal distribution. The special case of skew elliptical densities is examined in detail, establishing connections with existing similar work. The final part of the paper specializes further to a form of multivariate skew t-density. Likelihood inference for this distribution is examined, and it is illustrated with numerical examples.

1,215 citations

"Flexible Class of Skew‐Symmetric Di..." refers background in this paper

  • ...Finally, note that the stochastic representation of FSSdistributions follows from the stochastic representation of SS distributions described byWang et al. (2004), see also Azzalini & Capitanio (2003)....

    [...]

  • ...Similarly, multivariate distributions such as skew-t (Branco & Dey, 2001; Azzalini & Capitanio, 2003; Jones & Faddy, 2003; Sahu et al., 2003), skew-Cauchy (Arnold & Beaver, 2000) and other skewelliptical ones (Azzalini & Capitanio, 1999; Branco & Dey, 2001; Sahu et al., 2003) can be represented by…...

    [...]

  • ...Jones & Faddy (2003) and Azzalini & Capitanio (2003) fit two forms of skew-t distributions to these data....

    [...]

  • ...If each term has an odd order (all ks are odd), then the polynomial is called an odd polynomial, whereas if each term has an even order (all ks are even), it is called an even polynomial....

    [...]

Related Papers (5)
A class of distributions which includes the normal ones

[...]

01 Jan 1985-Scandinavian Journal of Statistics
Adelchi Azzalini
Distributions generated by perturbation of symmetry with emphasis on a multivariate skew t‐distribution

[...]

01 May 2003-Journal of The Royal Statistical Society Series B-statistical Methodology
Adelchi Azzalini, Antonella Capitanio
The multivariate skew-normal distribution

[...]

01 Dec 1996-Biometrika
Adelchi Azzalini, A. Dalla Valle
Skew-Elliptical Distributions and Their Applications : A Journey Beyond Normality

[...]

27 Jul 2004
Marc G. Genton
A General Class of Multivariate Skew-Elliptical Distributions

[...]

01 Oct 2001-Journal of Multivariate Analysis
Márcia D. Branco, Dipak K. Dey