A Flexible Class of Skew-Symmetri Distributions
(running head: exible skew-symmetri distributions)
YANYUAN MA
North Carolina State University
MARC G. GENTON
North Carolina State University
ABSTRACT. We prop ose a exible lass of skew-symmetri distributions for whih the
probability density funtion has the form of a pro dut of a symmetri density and a skewing
funtion. By onstruting an enumerable dense subset of skewing funtions on a ompat
set, we are able to onsider a family of distributions whih an apture skewness, heavy
tails, and multimo dality systematially. We present three illustrative examples for the
b er-glass data, simulated data from a mixture of two normal distributions, and Swiss
bills data.
Key Words:
dense subset; generalized skew-elliptial; multimodality; skewness; skew-normal.
1 Intro dution
A popular approah to ahieve departures from normality onsists of modifying the probability density
funtion (p df ) of a random vetor in a multipliative fashion. Wang, Boyer, & Genton (2004) showed
that any
p
-dimensional multivariate pdf
g
(
x
) admits, for any xed loation parameter
2
R
p
, a unique
skew-symmetri (SS) representation:
g
(
x
) = 2
f
(
x
)
(
x
)
;
(1)
where
f
:
R
p
!
R
+
is a symmetri p df and
:
R
p
!
[0
;
1℄ is a skewing funtion satisfying
(
x
) =
1
(
x
). Vie-versa, any funtion
g
of the type dened by (1) is a valid pdf. By symmetri, we mean
f
(
x
) =
f
(
x
) and we will use \symmetri pdf " and the prop erty
f
(
x
) =
f
(
x
) interhangeably in
the sequel. Throughout this pap er, we restrit our interest on funtions
f
2
C
0
(
R
p
) and ontinuous
skewing funtions
(
x
), where
C
0
(
R
p
) denotes ontinuous funtions on
R
p
with the prop erty
f
(
x
)
!
0
when
k
x
k
2
! 1
, and
k k
2
denotes the
L
2
norm. Genton & Lop erdo (2002) onsidered the subfamily
of generalized skew-elliptial (GSE) distributions for whih the p df
f
in (1) is elliptially ontoured
rather than only symmetri. Many denitions of skewed distributions found in the literature an be
written in the form of a skew-symmetri distribution (1). For instane, Azzalini & Dalla Valle's (1996)
multivariate skew-normal distribution orresp onds to
f
(
x
) =
p
(
x
;
0
;
) and
(
x
) = (
T
x
), where
p
(
x
;
;
) is the
p
-dimensional multivariate normal pdf with mean vetor
and orrelation matrix ,
1

is the standard normal umulative distribution funtion (df ), and
is a shap e parameter ontrolling
skewness. Similarly, multivariate distributions suh as skew-
t
(Brano & Dey, 2001; Azzalini & Capitanio,
2003; Jones & Faddy, 2003; Sahu, Brano, & Dey, 2003), skew-Cauhy (Arnold & Beaver, 2000) and
other skew-elliptial ones (Azzalini & Capitanio, 1999; Brano & Dey, 2001; Sahu
et al.
, 2003) an be
represented by the skew-symmetri distribution (1) with appropriate hoies of
f
and
.
In this artile, we prop ose a exible lass of distributions (1) by onstruting an enumerable dense
subset of the skewing funtions
on a ompat set. The result is a family of distributions whih
an apture skewness, heavy tails, and multimodality systematially. The onstrution of the subset is
through p olynomials, whih has a similar avor as the seminonparametri (SNP) representation prop osed
by Gallant & Nyhka (1987). The latter is dened as the pro dut of the standard normal p df and the
square of a polynomial. The SNP distribution requires the oeÆients in the polynomial to b e onstrained
in order to yield a valid density. It also relies on rejetion sampling shemes to simulate random samples.
These diÆulties do not o ur with our onstrution.
The ontent of the pap er is organized as follows. In Setion 2, we desribe a subset of skewing
funtions based on o dd p olynomials and prove that it results in a dense subset of the skew-symmetri
distributions. In partiular, we dene exible skew-normal and skew-
t
distributions that an have more
than one mode. This is an essential property for some situations and provides an alternative to modeling
with mixtures of distributions. The exibility and p ossible multimodality of the new lass of distributions
is illustrated in Setion 3. We present three illustrative examples in Setion 4, and a disussion in Setion
5.
2 A dense subset of skew-symmetri distributions
In this setion, we onstrut a dense subset of skew-symmetri distributions through approximating the
skewing funtion
on a ompat set. Any ontinuous skewing funtion
an be written as:
(
x
) =
H
(
w
(
x
))
;
(2)
where
H
:
R
!
[0
;
1℄ is the df of a ontinuous random variable symmetri around 0, and
w
:
R
p
!
R
is an o dd ontinuous funtion, that is
w
(
x
) =
w
(
x
). In fat, for a hosen
H
suh that
H
1
exists,
w
(
x
) =
H
1
(
(
x
)) is a ontinuous odd funtion. This representation has been used by Azzalini &
Capitanio (2003) to dene ertain distributions by p erturbation of symmetry. Note however that the
representation (2) is not unique due to the many possible hoies of
H
.
Let
P
K
(
x
) b e an o dd p olynomial of order
K
. A p olynomial of order
K
in
R
p
is dened as a linear
ombination of terms of the form
Q
p
i
=1
x
r
i
i
, where
k
=
P
p
i
=1
r
i
K
. If eah term has an odd order (all
k
's are o dd), then the polynomial is alled an odd p olynomial, whereas if eah term has an even order
(all
k
's are even), it is alled an even polynomial. We dene exible skew-symmetri (FSS) distributions
2

by restriting (1) to:
2
f
(
x
)
K
(
x
)
;
(3)
where
K
(
x
) =
H
(
P
K
(
x
)) and
H
is any df of a ontinuous random variable symmetri around 0. Note
that there are no onstraints on the oeÆients of the p olynomial
P
K
in order to make (3) a valid
pdf. In partiular, (3) denes exible generalized skew-elliptial (FGSE) distributions when the pdf
f
is
elliptially ontoured. For instane, exible generalized skew-normal (FGSN) distributions are dened
by:
2
p
(
x
;
;
)(
P
K
(
A
(
x
)))
;
(4)
and exible generalized skew-
t
(FGST) distributions are dened by:
2
t
p
(
x
;
;
;
)
T
(
P
K
(
A
(
x
));
)
;
(5)
where we use the Choleski deomposition
1
=
A
T
A
,
t
p
denotes a
p
-dimensional multivariate
t
pdf,
and
T
denotes a univariate
t
df, both with degrees of freedom
. Note that we ould use , or any
other symmetri df, instead of
T
for the skewing funtion in (5). In pratie, a popular hoie for the
df
H
would b e or the univariate df orresponding to the symmetri p df
f
. Eetively, the following
proposition shows that FSS distributions an approximate skew-symmetri distributions arbitrarily well.
Prop osition 1
Let the lass of exible skew-symmetri (FSS) distributions onsist of distributions with
pdf given in (3) and the lass of skew-symmetri (SS) distributions of distributions with pdf given in (1),
where
f
2
C
0
(
R
p
)
in both lasses and
is ontinuous. Then the lass of FSS distributions is dense in
the lass of SS distributions under the
L
1
norm.
Pro of
: An arbitrary distribution in the SS lass an be written as 2
f
(
x
)
H
(
w
(
x
)), where
f
and
H
are ontinuous,
H
1
exists, and
w
is a ontinuous o dd funtion. Beause
f
2
C
0
(
R
p
), for any arbitrary
>
0, we an nd a ompat set
D
whih is symmetri around
(if
x
2
D
then
x
2
D
), suh that
for any
x
=
2
D
,
f
(
x
)
< =
4. Thus, for any
x
=
2
D
,
j
2
f
(
x
)
(
x
)
2
f
(
x
)
H
(
P
((
x
))
j
<
for any odd p olynomial
P
.
Sine
f
is ontinuous,
f
is bounded on
D
. We denote the bound by
C
, i.e.
f
(
x
)
C
for any
x
2
D
. We use
D
1
to denote the image spae of
w
, i.e.
D
1
=
f
w
(
x
)
j
x
2
D
g
. Beause of the
ontinuity of
w
, whih is a result of the ontinuity of b oth
H
and
,
D
1
is also ompat. The ontinuous
funtion
H
is uniformly ontinuous on the ompat set
D
1
. Hene there exists
>
0 suh that for
any
y
1
,
y
2
2
D
1
and
j
y
1
y
2
j
<
, we get
j
H
(
y
1
)
H
(
y
2
)
j
< =
(2
C
). From the Stone-Weierstrass
theorem (see e.g. Rudin, 1973, p. 115), there exists a polynomial
P
suh that
j
w
(
x
)
P
(
x
)
j
<
for any
x
2
D
. We deomp ose
P
into an even term
P
e
and an odd term
P
o
, i.e.
P
=
P
e
+
P
o
.
Then
j
w
(
x
)
P
e
(
x
)
P
o
(
x
)
j
<
and
j
w
(
x
)
P
e
(
x
)
P
o
(
x
)
j
<
. Beause
w
and
P
o
are odd, and
P
e
is even, we get
j
w
(
x
)
P
e
(
x
) +
P
o
(
x
)
j
<
. Notie that
2
j
w
(
x
)
P
o
(
x
)
j j
w
(
x
)
P
e
(
x
)
P
o
(
x
)
j
+
j
w
(
x
)
P
e
(
x
) +
P
o
(
x
)
j
<
2
,
3

so
j
w
(
x
)
P
o
(
x
)
j
<
. Combining these results, we know that for an arbitrary member
2
f
(
x
)
H
(
w
(
x
)) in SS and an arbitrary
>
0, we an nd a member 2
f
(
x
)
H
(
P
o
(
x
)) in
FSS suh that
j
2
f
(
x
)
H
(
w
(
x
))
2
f
(
x
)
H
(
P
o
(
x
))
j
<
for any
x
2
D
.
Hene FSS is dense in SS with resp et to the
L
1
norm.
Remark 1
The requirement
f
2
C
0
(
R
p
)
in proposition 1 an be relaxed to al low that
f
has a nite
number,
m
say, of poles. In this ase, FSS is dense in SS with respet to almost uniform onvergene
(uniform in a set whose omplement is of measure arbitrarily smal l). Indeed, let
R
p
(
r
)
denote
R
p
minus
the union of
m
open bal ls of radius
r
entered at the
m
poles. Then FSS is dense in SS on
R
p
(
r
)
under
the
L
1
norm. Letting
r
!
0
, the result fol lows.
Proposition 1 shows in partiular that the lass of generalized skew-elliptial, skew
t
, and skew-
normal distributions an b e approximated arbitrarily well by their exible versions.
3 Flexibility and multimodality
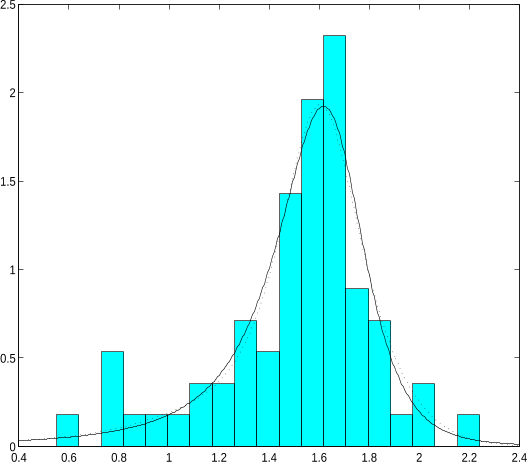
In Figure 1, we illustrate the shap e exibility of the FGSN distribution in the univariate ase. Its pdf
for
K
= 3 is dened by:
2
1
(
x
;
;
2
)(
(
x
)
=
+
(
x
)
3
=
3
)
:
(6)
Figure 1 should b e here.
Figure 1(a) depits the p df of the FGSN model for
= 0,
2
= 1,
= 4, and
= 0, i.e. it redues
to Azzalini's (1985) univariate skew-normal distribution. However, when
6
= 0, the p df (6) an exhibit
bimodality as shown in Figure 1(b) with
= 1, and
=
1. In general, as the degree
K
of the o dd
polynomial in the skewing funtion beomes large, the number of mo des allowed in the p df inreases,
thus induing a greater exibility in the available shapes. Unfortunately, the number of modes depends
on the degree
K
of the o dd p olynomial, on the symmetri pdf
f
, and on the df
H
of the skewing
funtion
K
in a omplex fashion. Indeed, even for the univariate situation given by
p
= 1, the mo des
are determined by zeros of the rst derivative of the FSS distribution (3) given by:
2
f
0
(
x
)
H
(
P
K
(
x
)) + 2
f
(
x
)
H
0
(
P
K
(
x
))
P
0
K
(
x
)
;
(7)
for whih the number of zeros annot b e easily omputed. Even with restritions to some sp ei
f
and
H
funtions, a general statement on the relation between the number of mo des and the order of the
polynomial seems not available. However, in the univariate ase, if we onsider a normal pdf
f
=
1
and
a standard normal df
H
= with an o dd p olynomial of order
K
= 3, we have the following proposition.
Prop osition 2
The lass of exible generalized skew-normal (FGSN) distributions with pdf
2
1
(
x
;
;
2
)(
(
x
)
=
+
(
x
)
3
=
3
)
has at most 2 modes.
4

Pro of
: Without loss of generality, we an set
= 0,
= 1, assume
>
0, and only need to prove that
(
x
) = 2
(
x
)(
x
+
x
3
) has at most two modes. We prove this by ontradition. If
(
x
) has more
than two mo des, then
0
(
x
) has at least ve zeros. In the following pro of, we show that this annot b e
the ase. We have
0
(
x
) = 2
(
x
)((
+ 3
x
2
)
(
x
+
x
3
)
x
(
x
+
x
3
)) and need to onsider three
ases:
ase 1:
= 0
We write
0
(
x
) = 2
x
(
x
)
(
x
), where
(
x
) = 3
x
(
x
3
)
(
x
3
). We an verify that
0
(
x
) =
3
(
x
3
)
1
(
y
) where
y
=
x
2
and
1
(
y
) = 1
y
3
2
y
3
. Sine
1
(
y
) is a dereasing funtion on
y
0,
0
(
x
) has at most two zeros. Thus,
(
x
) has at most three zeros, hene
0
(
x
) has at most four
zeros.
ase 2:
>
0
Notie that
0
(
x
)
>
0 for
x
0. For
1
(
x
) =
0
(
x
)
=
(2
x
(
x
)) =
(
x
+
x
3
)(
+ 3
x
2
)
=x
(
x
+
x
3
),
we get
0
1
(
x
) =
(
x
+
x
3
)
=
(
9
x
2
)
2
(
y
), where
y
=
+ 3
x
2
>
0 and
2
(
y
) =
y
4
+
y
3
+ (3
2
2
)
y
2
(3
+ 9
)
y
+ 18
. Sine
00
2
(
y
) = 12
y
2
+ 6
y
+ (6
4
2
) has at most 1 positive zero, and
0
2
(
y
) = 4
y
3
+ 3
y
2
+ (6
4
2
)
y
(3
+ 9
)
<
0 at
y
= 0, we know that
0
2
(
y
) has at most one positive
zero. Thus
2
(
y
) has at most 2 positive zeros. This means
0
1
(
x
) has at most two p ositive zeros, so
0
(
x
)
has at most three (p ositive) zeros.
ase 3:
<
0
Notie that
0
(
x
)
<
0 for
x
2
[0
;
p
=
(3
) ℄ and
0
(
x
)
>
0 for
x
2
(
1
;
p
=
(3
) ℄. So we only
look for solutions
x
2
(
p
=
(3
)
;
1
) and
x
2
(
p
=
(3
)
;
0). Let
y
=
+ 3
x
2
, then there is a one
to one mapping b etween the
x
in the ab ove range and
y
2
(
;
1
). Let
1
(
x
) and
2
(
y
) have the same
expressions as in ase 2. We have that
2
(
y
) has at most four zeros sine it is a fourth order p olynomial.
Notie that
2
(
)
<
0
;
2
(
1
)
>
0, so
2
(
y
) has at most three zeros in (
;
1
). This means
0
1
(
x
) has
at most three zeros, hene
0
(
x
) has at most four zeros.
Figure 1 illustrates the result of prop osition 2 by depiting a unimo dal and a bimo dal pdf from the
univariate FGSN with
K
= 3. For
K
= 1, the p df is always unimodal as was already noted by Azzalini
(1985) for the univariate skew-normal distribution.
Next we investigate the exibility of the FGSN distribution in the bivariate ase. Its pdf for
K
= 3,
=
0
, and =
I
2
is given by:
2
2
(
x
1
; x
2
;
0
; I
2
)(
1
x
1
+
2
x
2
+
1
x
3
1
+
2
x
3
2
+
3
x
2
1
x
2
+
4
x
1
x
2
2
)
:
(8)
Figure 2 should b e here.
Figure 2 depits the ontours of four dierent pdfs (8) for various ombinations of values of the
skewness parameters
1
,
2
,
1
,
2
,
3
, and
4
. In partiular, for
1
=
2
=
3
=
4
= 0, the
pdf is exatly the bivariate skew-normal proposed by Azzalini & Dalla Valle (1996), and known to be
unimodal, see Figure 2(a). However, Figures 2(b)-(d) show that many dierent distributional shap es an
be obtained with the parameters
1
; : : : ;
4
, in partiular bimodal and trimo dal distributions. Additional
5