![FIG. 7. (Color online) The steady-state probability distribution of the two-motor model as a function of a reduced sampling rate ku. At a reduction of ≈0.05 times the initial value, the highest steady-state probability does not belong to the center-positioned intermediate anymore. The distribution turns from a monomodal to a bimodal behavior. The considered system has an ATP concentration of 20μM with a rough approximation for kc and kI and high processivity (see [5]).](/figures/fig-7-color-online-the-steady-state-probability-distribution-1lqlg5nq.webp)
![FIG. 2. The two-motor model with a power stroke is schematically depicted with transitions between the five chemical states. The chemical states (0,0), (ATP,0), (0,ATP), (ADP*Pi,0), and (0,ADP*Pi) are numbered from 1 to 5, respectively. The rate kw(ℓ) [or k ′ w(ℓ)] is the length-dependent transition rate from the (ATP,0) [or (0,ATP)] state to the active translocation state (ADP*Pi,0) [or (0,ADP*Pi)]. The rate ktr , assumed to be length independent, is the transition rate from the active translocation state [(ADP*Pi,0) or (0,ADP*Pi)] to the apo state (0,0). The rate kp is the ATP binding rate from the (0,0) to the (ATP,0) [or (0,ATP)] state. Finally, the rate kp,s is the transition rate which makes ATP sampling possible; it is the ATP unbinding rate of the left (or right) motor to the apo state, with the possibility of subsequent binding to the right (or left) motor.](/figures/fig-2-the-two-motor-model-with-a-power-stroke-is-13h72c4u.webp)
![FIG. 9. (Color online) The circle-line approximation, following Ref. [22]. Loop opening angle α, excess loop length L, exposed loop length L∗, nucleosomal radius R, and loop curvature κ = 1/r .](/figures/fig-9-color-online-the-circle-line-approximation-following-2xwdsye3.webp)
HAL Id: hal-03172871
https://hal.univ-lille.fr/hal-03172871
Submitted on 17 May 2021
HAL is a multi-disciplinary open access
archive for the deposit and dissemination of sci-
entic research documents, whether they are pub-
lished or not. The documents may come from
teaching and research institutions in France or
abroad, or from public or private research centers.
L’archive ouverte pluridisciplinaire HAL, est
destinée au dépôt et à la diusion de documents
scientiques de niveau recherche, publiés ou non,
émanant des établissements d’enseignement et de
recherche français ou étrangers, des laboratoires
publics ou privés.
Fokker-Planck description of single nucleosome
repositioning by dimeric chromatin remodelers
Yves Vandecan, Ralf Blossey
To cite this version:
Yves Vandecan, Ralf Blossey. Fokker-Planck description of single nucleosome repositioning by dimeric
chromatin remodelers. Physical Review E : Statistical, Nonlinear, and Soft Matter Physics, American
Physical Society, 2013, Physical Review. E, Statistical, Nonlinear, and Soft Matter Physics, 88 (1),
pp.012728. �10.1103/PhysRevE.88.012728�. �hal-03172871�
PHYSICAL REVIEW E 88, 012728 (2013)
Fokker-Planck description of single nucleosome repositioning by dimeric chromatin remodelers
Yves Vandecan and Ralf Blossey
Interdisciplinary Research Institute USR 3078 CNRS and Universit
´
e de Sciences et de Technologies de Lille, Parc de la Haute Borne,
50 Avenue de Halley, 59658 Villeneuve d’Ascq, France
(Received 18 January 2013; published 30 July 2013)
Recent experiments have demonstrated that the ATP-utilizing chromatin assembly and remodeling factor (ACF)
is a dimeric, processive motor complex which can move a nucleosome more efficiently towards longer flanking
DNA than towards shorter flanking DNA strands, thereby centering an initially ill-positioned nucleosome on
DNA substrates. We give a Fokker-Planck description for the repositioning process driven by transitions between
internal chemical states of the remodelers. In the chemical states of ATP hydrolysis during which the repositioning
takes place a power stroke is considered. The slope of the effective driving potential is directly related to ATP
hydrolysis and leads to the unidirectional motion of the nucleosome-remodeler complex along the DNA strand.
The Einstein force relation allows us to deduce the ATP-concentration dependence of the diffusion constant
of the nucleosome-remodeler complex. We have employed our model to study the efficiency of positioning of
nucleosomes as a function of the ATP sampling rate between the two motors which shows that the synchronization
between the motors is crucial for the remodeling mechanism to work.
DOI: 10.1103/PhysRevE.88.012728 PACS number(s): 87.14.gk, 87.15.A−,87.16.Nn
I. INTRODUCTION
Nucleosome repositioning on DNA substrates can be
spontaneous due to thermal fluctuations or forced by adenosine
triphosphate–(ATP-) dependent remodelers [
1,2]. Recently,
in vitro experiments and structural analyses have shown
the ATP-utilizing chromatin assembly and remodeling factor
(ACF) to be a dimeric, processive motor which generates
center-positioned nucleosomes because it moves the nucle-
osome more efficiently towards the longer flanking DNA than
towards the shorter flanking DNA strands [
3,4]. A schematic
representation is shown in Fig. 1.
In previous work, we have formulated a stochastic model for
this positioning process based on a master equation approach
[5]. Although this model predicts reliable velocity profiles
and dispersions and furthermore made explicit some details
of the fueling mechanism of the ACF motors along with their
synchronization, the basic mechanism proposed considers only
transitions between discrete intermediate states without any
mechanical knowledge of the motor. Despite the fact that
discrete intermediates are observed in gel mobility shift ex-
periments, the dynamical frequency resonance energy transfer
(FRET) time traces show translocation steps of 7 base pairs
(bp), 3 bp, and again 3 bp with finite translocation step times.
Here, we propose a continuous repositioning mechanism in
terms of a Fokker-Planck equation which, beyond the discrete
two-motor model, allows explicit treatment of the thermal
diffusion of the nucleosome-remodeler complex. A second
aspect is the application of both models to the centering of
a nucleosome-remodeler complex as a function of the ATP
sampling between the two motors, a situation of relevance
for the interpretation of the experimental findings by Narlikar
[
3,4].
In our Fokker-Planck (FP) model, we retain the explicit
description of the two motors as used previously in Ref. [
5],
but we now require the knowledge of the potentials belonging
to the chemical states. The FP model allows for a detailed
chemomechanical description of the motors, although no
experimental effective driving potential [
6] of ACF has been
derived so far in the literature. We assume that in the
chemical states of ATP hydrolysis (the activated ADP*Pi
states in Ref. [
3]) basic effective driving potentials are acting
which, as will be seen later on, are capable of centering
the nucleosome with respect to the DNA substrate. These
effective driving potentials are purely power stroke potentials
in which the chemical energy of ATP hydrolysis is converted
into mechanical work done along a motor step [
7]. Experi-
mentally, the ability of chromatin remodelers to translocate
nucleosomes under high forces points to a motor with a power
stroke mechanism rather than a Brownian ratchet mechanism
rectifying (large) thermal fluctuations [6,8,9], which motivates
our choice.
The origin of power strokes is related to the tightening of
the remodeler with DNA, pulling the DNA flanking length
into the nucleosome [
8,10] and “tracking” of the nucleosome-
remodeler complex with respect to the DNA. This means that
the motor translocates along the DNA, and ATP is required for
the unidirectional diffusion of the bulge towards the distal end
of the nucleosome. The energy release of ATP hydrolysis,
required for a translocation of size ℓ, corresponds to a
potential energy decrease U
d
. The parameter ℓ determines
the position of the nucleosome with respect to the DNA
strand. Based on experimental findings, one ATP molecule
is consumed, releasing 12k
B
T during ATP hydrolysis [
11],
for a 13 bp translocation [
12]. The slope of the power stroke
potential U
d
/ℓ equals a generated force F ≈ k
B
T/bp.
The other remaining chemical states, with a reduced
remodeler-DNA interaction [
10], are mainly governed by
the thermal motion of DNA. These thermal fluctuations
are incorporated in the thermal diffusion constant of the
nucleosome-remodeler complex, D
NR
, which can be due
to twist or loop diffusion. Experimental thermal diffusion
constants of the nucleosome without the presence of the (ACF)
remodeler D are in the order of 1 bp
2
/s. The diffusion of
10 bp loops results in the rather low theoretical value of D =
0.1bp
2
/s while twist diffusion, in combination with a position-
ing sequence, predicts a higher value of D = 7bp
2
/s [
2,13].
012728-1
1539-3755/2013/88(1)/012728(8) ©2013 American Physical Society
YVES VANDECAN AND RALF BLOSSEY PHYSICAL REVIEW E 88, 012728 (2013)
FIG. 1. (Color online) Schematic representation of the geometry
of the ACF-nucleosome complex. The nucleosome is shown as a
cylinder, on which two remodelers are placed with their central
motor unit, while the directional domain (SANT-SLIDE), presented
as a rectangle, attaches to the linker DNA. The displacement of the
complex is controlled by the synchronization of the two remodelers.
Using the theoretical Einstein force scale [
11], we estimate
the thermal diffusion constant of the nucleosome-remodeler
(NR) complex to be D
NR
= (k
B
T/F)V , via the experimental
local translocation speed V in the frequency resonance energy
transfer time traces. We quantify V by (13 bp)k
tr
, with 1/k
tr
as the effective translocation time required to translocate 13 bp
along the DNA strand [
5]. Although the Einstein force scale
is strictly only valid for Brownian particle motion in thermal
equilibrium, its application to an activated molecular motor
ACF still yields acceptable results [
11]. These computations
reveal an ATP dependence of the diffusion constant of the
nucleosome-remodeler complex, with a higher mobility at
higher ATP concentrations. The latter refers to ATP-dependent
looping and possibly reflects a remodeler-mediated looping
mechanism depending on the concentration of ATP, as exper-
imentally suggested [
14,15].
Our paper is organized as follows: We derive a system of
five coupled Fokker-Planck equations which represent the time
evolution of the probability functions to be in the correspond-
ing five chemical states. Next, a comparative study of this
continuum model with the discrete motor models is presented,
in which we discuss the similarities, (dis)advantages, and
insights of our Fokker-Planck model. We close with a detailed
discussion of the ATP dependence of the diffusion constant.
II. A FOKKER-PLANCK MODEL OF ACF
REPOSITIONING
In considering a highly processive motor we restrict our
analysis to the actual repositioning process without dissoci-
ation of the nucleosome-remodeler complex. Five chemical
states are considered to describe the repositioning process by
dimeric ACF. We catalog the states of the two motors by a
two-valued variable in which each value represents the state
of an individual motor. The first chemical state is an apo
state (0,0) without ATP binding. The next two chemical states
are (ATP,0) and (0,ATP) with ATP bound to the left (right)
ATPase unit bound at nucleosomal superhelical locations
(−2,2), respectively. The remaining two states correspond to
ATP in activated form, i.e., (ADP*Pi,0) and (0,ADP*Pi) in
which the left (right) motor translocates the complex along
the DNA strand, decreasing the ATP energy. The transition
scheme of these chemical states is shown in Fig.
2.
ATP, 0
0, ATP
ADP*Pi, 0
0, ADP*Pi
0 , 0
k
k
k
k
k
k
k
k
p,s
p
p
p,s
w
w
tr
tr
1
1
2 3
4
5
,
FIG. 2. The two-motor model with a power stroke is schemati-
cally depicted with transitions between the five chemical states. The
chemical states (0,0), (ATP,0), (0,ATP), (ADP*Pi,0), and (0,ADP*Pi)
are numbered from 1 to 5, respectively. The rate k
w
(ℓ)[ork
′
w
(ℓ)] is
the length-dependent transition rate from the (ATP,0) [or (0,ATP)]
state to the active translocation state (ADP*Pi,0) [or (0,ADP*Pi)].
The rate k
tr
, assumed to be length independent, is the transition rate
from the active translocation state [(ADP*Pi,0) or (0,ADP*Pi)] to the
apo state (0,0). The rate k
p
is the ATP binding rate from the (0,0) to
the (ATP,0) [or (0,ATP)] state. Finally, the rate k
p,s
is the transition
rate which makes ATP sampling possible; it is the ATP unbinding
rate of the left (or right) motor to the apo state, with the possibility of
subsequent binding to the right (or left) motor.
The transition rate k
p
is for the transition from the apo
state to (ATP,0) or (0,ATP). The rate k
p,s
corresponds to the
unbinding of ATP from (ATP,0) or (0,ATP) without being
hydrolyzed. The former rate is related to ATP-loading steps
while the latter introduce the sampling step between the motors
in which a nonhydrolyzed ATP is unbound from the “left”
motor and can be bound to the “right” motor or vice versa,
which is why we also call this rate the “sampling rate.” The
rates k
w
(ℓ) and k
′
w
(ℓ) correspond to the ATP “activation”
time to initiate ATP hydrolysis, allosterically dependent on
the DNA linker length ℓ [
16]. From these FRET experiments
of nucleosomes with different flanking lengths, a plot of the
natural logarithm of the rate constant ln(k), proportional to the
activation energy of the reaction, versus their DNA flanking
length is a straight line. In our model, we assume for the
activation time an exponential dependence on the linker length
ℓ, i.e.,
k
w
(ℓ) = αe
a(80−ℓ)
, (1)
k
′
w
(ℓ) = αe
aℓ
, (2)
where a = 0.077 bp
−1
[
5] is the intrinsic linker length depen-
dence, α a proportionality constant, and the linker length ℓ
varies between 0 and 80 bp. The end-positioned nucleosomes
0N80 and 80N 0 correspond to ℓ = 0,80 bp. Between these
extreme values of ℓ, all other DNA linker lengths are possible.
In the case of the end-positioned nucleosome 0N80 (ℓ = 0),
the activation time rate k
w
(ℓ) of the (ATP,0) to (ADP*Pi,0)
state differs by an exponential factor from the rate k
′
w
(ℓ)ofthe
(0,ATP) to the (0,ADP*Pi) state [
5]. Concerning the motion
of the remodeler-nucleosome complex, suppose we have an
end-positioned nucleosome ℓ = 0: Starting from the apo state,
ATP can bind to the left or to the right motor, i.e., the (ATP,0)
or (0,ATP) state. In the (ATP,0) the activation rate k
w
(ℓ = 0)
has a high value so that the nucleosome-remodeler complex
012728-2
FOKKER-PLANCK DESCRIPTION OF SINGLE ... PHYSICAL REVIEW E 88, 012728 (2013)
probably enters (ADP*Pi,0) before dissociating to the apo
state, while in the (0,ATP) state k
′
w
(ℓ = 0) is practically zero,
and therefore ATP will with high probability to dissociate
before entering the (0,ADP*Pi) state. As a consequence, the
nucleosome-remodeler complex is pushed towards larger ℓ.
Finally, the rate k
tr
is the inverse of the period during which
the active translocation takes place due to ATP hydrolysis. We
remark that the total rates k (k
′
) from [(ATP,0) (0,ATP)] to the
apo state (0,0) equal
k =
αe
a(80−ℓ)
1 +
α
k
tr
e
a(80−ℓ)
, (3)
k
′
=
αe
aℓ
1 +
α
k
tr
e
aℓ
. (4)
For
α
k
tr
≪ 1 and small values of ℓ,Eq.
(4) reduces to
the experimental transition rates of the form k
0
e
aℓ
,20 ℓ
60 bp, between the intermediates in the previous one- and
two-motor models [
5]. The factor α can thus be approximated
by the value of k
0
in previous work. Importantly, the equation
for k
′
has the proper shape to saturate at higher values of
ℓ, resembling the cutoff at 60 bp discussed in the previous
model. A similar reasoning can be used for k. The exponential
dependence of only the activation time on the DNA linker
length, and not the translocation time (1/k
tr
) itself (to less
extent), consequently has experimental justification. Hydroxyl
radical footprint studies show that, after ATP binding, the
remodeler interaction with the DNA flanking length increases
its protection pattern (i.e., the covering of the DNA substrate),
allosterically triggering ATP hydrolysis [
10,16].
Once the transitions between the chemical states are de-
fined, the dynamics can be translated into five coupled Fokker-
Planck equations that allow computation of the probability
distributions P
σ
(ℓ,t) of the five chemical states, σ = 1,...,5
(see Fig.
2), as a function of the ℓ state and time t. The five
coupled partial differential equations for P
σ
(ℓ,t) can be written
as
∂
t
P
σ
(ℓ,t) + ∂
ℓ
J
σ
(ℓ,t) =
5
σ
′
=1
M
σσ
′
P
σ
′
(ℓ,t), (5)
with the probability flux
J
σ
(ℓ,t) =−
1
γ
∂
ℓ
U
σ
(ℓ)P
σ
(ℓ,t) − D
NR
∂
ℓ
P
σ
(ℓ,t). (6)
Here U
σ
(ℓ) is the potential (as a function of ℓ) in the chemical
state σ ; see Fig.
3. Further, D
NR
denotes the thermal diffusion
constant of the nucleosome-remodeler complex, the friction
coefficient γ = k
B
T/D
NR
, and M
σσ
′
the matrix elements of
M =
⎛
⎜
⎜
⎜
⎝
−2k
p
k
p,s
k
p,s
k
tr
k
tr
k
p
−k
w
(ℓ) − k
p,s
000
k
p
0 −k
′
w
(ℓ) − k
p,s
00
0 k
w
(ℓ)0−k
tr
0
00 k
′
w
(ℓ)0−k
tr
⎞
⎟
⎟
⎟
⎠
.
The presumed expressions for the potentials U
4
(ℓ) and
U
5
(ℓ) in the activated states (ADP*Pi,0) and (0,ADP*Pi)
are ∓(k
B
T/bp)ℓ, respectively, and thus proportional to the
linker length ℓ. The decreasing (or increasing) straight lines
are pure power stroke potentials, tracking the complex in a
definite direction of ℓ with the ATP energy consumption along
U( )
k T
B
(bp)
ATP-
energy
release
motor
step
FIG. 3. The potential U (ℓ) in the Fokker-Planck equation.
the straight line. The slopes of the power stroke potentials
U
4
(ℓ) and U
5
(ℓ)are∓k
B
T/bp. The latter expressions are
based on the experimental fact that a motor step size of
13 bp corresponds to an energy decrease of 12k
B
T , the energy
release due to ATP hydrolysis of one ATP molecule [
11,12].
The remaining potentials for σ
′
= 1,2,3 vanish identically.
In the discussion of the mathematical technique to solve the
equations, given below, the zero-flux boundary conditions are
replaced by an extension of the ℓ states and the introduction
of an artificial confinement potential. We further introduce the
total probability distribution
P
t
(ℓ,t) =
5
σ =1
P
σ
(ℓ,t). (7)
It is interesting to note that, from the Fokker-Planck
equations which describe a continuous stochastic process, we
are able to go back to an equivalent master equation, describing
a jump process [
17]. In our case, this can be achieved
by allowing only transitions between the chemical states at
definite ℓ = ℓ
i
states. For example, if transitions at each base
pair are considered, then we end up with an equivalent master
equation modeling transitions among 160 × 5 states.
We expect the remodeler to be incapable of translocating
with too short DNA linker lengths, so that for these ℓ states
the power stroke potentials U
4
(ℓ) and U
5
(ℓ) should be flat.
However, the states with too short linker lengths will not be
reached due to the inability for ATP hydrolysis. In order to
simplify the calculations, we may assume U
4
(ℓ) and U
5
(ℓ)
equal to ∓(k
B
T/bp)ℓ for all ℓ states without much affecting
the numerical outcome.
Concerning the translocation step time and the kinetic
pauses from the FRET time traces [
14], we presume an
effective 13 bp translocation step time (sum of the experimental
7 bp, 3 bp, and 3 bp translocation step times) and an effective
pause (sum of the experimental first, second, and third kinetic
pauses), as in Ref. [
5]. The thermal diffusion constant of
the nucleosome-remodeler complex, D
NR
, equals (k
B
T/F)V
012728-3
YVES VANDECAN AND RALF BLOSSEY PHYSICAL REVIEW E 88, 012728 (2013)
TABLE I. Estimated values of the model parameters as functions
of the ATP concentration [
5,14].
[ATP] (μM) α = k
0
(min
−1
) k
tr
(s
−1
) k
p
(s
−1
) D
NR
(bp
2
/s)
2 0.02 0.03 0.03 0.4
20 0.3 0.5 0.3 6.5
200 0.5 0.8 0.6 11
2000 0.6 1 0.9 13
using the Einstein force scale. The generated force F =
U
d
/ℓ is theoretically determined by the energy release
U
d
of one molecule of ATP during a translocation ℓ =
13 bp. The local translocation speed V = (13 bp)k
tr
is ob-
tained via the experimentally established effective translo-
cation time 1/k
tr
. If we again set the sampling rate k
p,s
equal to k
p
, then the ATP loading rates k
p
(and k
p,s
)inthis
Fokker-Planck model are found from
t
k
=
2
k
p
+
1
k
w
(0)
, (8)
with t
k
as the effective kinetic pause. k
w
(0) is the activation
time rate [see formula
(1)] of the end-positioned nucleosome
needed to address the experimental FRET time traces. A
summary of the computed model parameters for different
values of ATP is given in Table I.
In order to numerically solve the coupled Fokker-Planck
equations, we employ a simple finite difference method. At
time t
i
and spatial position ℓ
p
, the derivative ∂
ℓ
P
σ
(ℓ
p
,t
i
) and
the second derivative ∂
2
ℓ
P
σ
(ℓ
p
,t
i
) are numerically computed
by the centered-difference approximation,
∂
ℓ
P
σ
(ℓ
p
,t
i
) =
P
σ
(ℓ
p
+ ℓ,t
i
) − P
σ
(ℓ
p
− ℓ,t
i
)
2ℓ
+ O(ℓ
2
), (9)
∂
2
ℓ
P
σ
(ℓ
p
,t
i
)
=
P
σ
(ℓ
p
+ ℓ,t
i
) − 2P
σ
(ℓ
p
,t
i
) + P
σ
(ℓ
p
− ℓ,t
i
)
ℓ
2
+ O(ℓ
2
). (10)
Next we can compute the corresponding increment P
σ
(ℓ
p
,t
i
)
by ∂
t
P
σ
(ℓ
p
,t
i
)t and applying Eq.
(5). Instead of imposing
more complicated zero-flux boundary conditions, we extend
the interval for ℓ from [0, 80] to [0 − δ
I
,80 + δ
I
], and put
the system in a confinement potential (see the Appendix),
preventing a probability flux at the boundaries. The bound-
ary condition P (0 − δ
I
,t) = P (80 + δ
I
,t) = 0 for all t then
conceptually suffices to conserve total probability within the
confinement potential. In the numerical computations δ
I
is
set to 40 bp. As a measure for the numerical accuracy, we
check the conservation of the total probability as a function
of the time. A spatial step x = 0.5 bp and time steps
t = 0.02 and 0.001 s for 2, 20 200, and 2000 μMATP,
respectively, produce an approximate numerical solution that
leaves the total probability unaltered within a 0.2% “band”
around probability 1 among the ℓ states. An increase in
accuracy narrows this band, but also significantly enlarges
the numerical computation time. (A general disadvantage
of the FP model is that it can only be solved numerically
and not exactly, as could be done with the master equation
model.) As can be easily checked numerically, stationary
probability distributions are rather insensitive to distinct step
sizes. Stationary probability distributions, because they are
generally independent of the initial distribution, have the
advantage to find first a rough approximate expression with
less accurate step sizes, after which a numerically accurate
stationary distribution is obtained with refined step sizes.
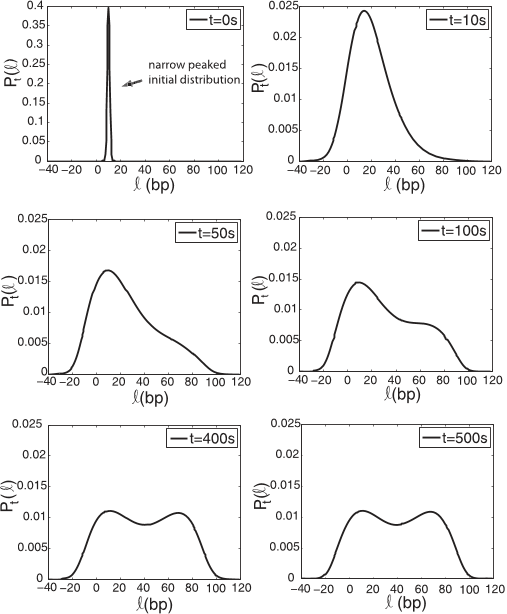
III. RESULTS AND DISCUSSION
A. Velocity profiles
For our Fokker-Planck model we use the finite difference
approximation scheme described above to compute the prob-
ability density functions P
t
(ℓ,t) for the four concentrations of
ATP given in Table
I. As initial distribution for the probability
distribution we choose
P
t
(ℓ,t = 0) =
1
2πσ
2
exp
−
(ℓ − 10)
2
2σ
2
, (11)
reflecting a family of nucleosomes (nearly end positioned)
around a mean ℓ = 10 bp, with a standard deviation σ = 1 bp.
The average velocity profiles v (see Fig.
4) are obtained by
numerical integration of the expression
v=
d
dt
ℓ
f
ℓ
i
dℓ P
t
(ℓ,t)ℓ, (12)
with ℓ
i
and ℓ
f
the values of the initial and the final ℓ
states, respectively. The velocity profiles from the continuum
model [see Fig.
4(a)] are similar to our two previous motor
models (single motor and two motors) with transitions between
the seven intermediates [5]. A family of end-positioned
nucleosomes around the mean ℓ = 0, but allowing for negative
ℓ states, returns velocity profiles that overall coincide better
with the previous discrete two-motor model, as they should
[see Fig. 4(b)]. This accordance justifies the assumptions of
the underlying physics in the Fokker-Planck model, opening
a more detailed level of the physical description of the
remodeling mechanism by the ACF: (1) The energy release
per ATP molecule contributes to an average translocation of
13 bp; (2) the separate implementation of the ATP consumption
required for centering or localizing the nucleosome with
respect to DNA, and of the thermal fluctuations via the thermal
diffusion constant; (3) the ATP concentration dependence of
the diffusion constant of the nucleosome-remodeler complex
D
NR
; and (4) the argument that the activation time (to enter the
ADP*Pi state) is exponentially dependent on the linker length
ℓ and not (or to less extent) the lifetime of the ADP*Pi state
itself—but certainly on this point more experimental evidence
is called for. So far, there exists no experimental evidence as
to which step of the ATPase cycle the DNA flanking length
participates in Ref. [
4].
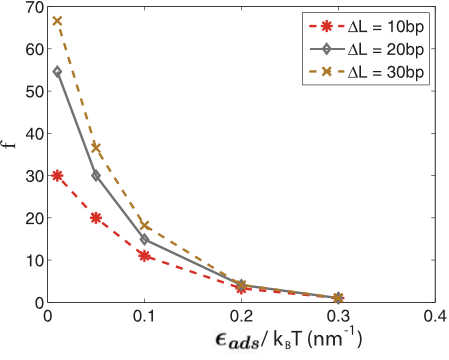
B. Sampling between the motors
In our previous paper [
5], we showed that a proper sampling
rate is required for center positioning of the nucleosome with
respect to the DNA strand. Here we go one step further.
In order to quantify the importance of sampling, or when
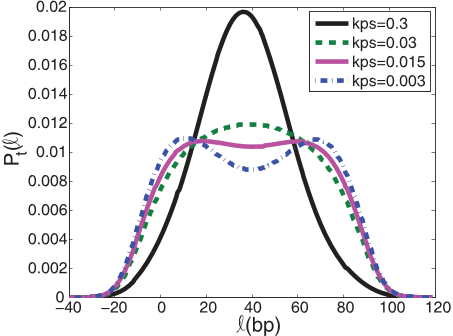
the desynchronization becomes appreciable, we examine the
012728-4